7.4: Розподільна власність

Цілі навчання

• Спрощення виразів за допомогою властивості distributive
• Оцінити вирази за допомогою розподільної властивості

будьте готові!

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Множимо: 3 (0,25). Якщо ви пропустили цю проблему, перегляньте приклад 5.3.5
2. Спрощення: 10 − (−2) (3). Якщо ви пропустили цю проблему, перегляньте приклад 3.7.5.
3. Поєднуйте як терміни: 9y + 17 + 3y − 2. Якщо ви пропустили цю проблему, перегляньте приклад 2.3.10.

Спрощення виразів за допомогою властивості розподілу

Припустимо, троє друзів збираються в кіно. Кожному з них потрібно $9.25; тобто 9 доларів і 1 квартал. Скільки грошей їм потрібно всім разом? Можна подумати про доларах окремо від кварталів.

Їм потрібно 3 рази $9, так $27, і 3 рази 1 квартал, так 75 центів. Всього їм потрібно $27,75. Якщо ви думаєте про те, щоб зробити математику таким чином, ви використовуєте розподільну властивість.

Визначення: Розподільна власність

Якщо a, b, c - дійсні числа, то a (b + c) = ab + ac.

Повернувшись до наших друзів у фільмах, ми могли б показати математичні кроки, які ми робимо, щоб знайти загальну суму грошей, яка їм потрібна, як це:

$$\begin{split} 3(9&.25) \\ 3(9 &+ 0.25) \\ 3(9) &+ 3(0.25) \\ 27 &+ 0.75 \\ 27&.75 \end{split}$$

В алгебрі ми використовуємо властивість Distributive для видалення дужок, оскільки ми спрощуємо вирази. Наприклад, якщо нас попросять спростити вираз 3 (x + 4), порядок операцій говорить працювати в дужках спочатку. Але ми не можемо додати х і 4, оскільки вони не схожі на терміни. Таким чином, ми використовуємо розподільну властивість, як показано в прикладі$\PageIndex{1}$.

Приклад$\PageIndex{1}$:

Спрощення: 3 (x + 4).

Рішення

Розподілити.	3 • х + 3 • 4
Помножити.	3х + 12

Вправа$\PageIndex{1}$:

Спрощення: 4 (x + 2).

Відповідь

$4x+8$

Вправа$\PageIndex{2}$:

Спрощення: 6 (x + 7).

Відповідь

6х + 42

Деякі студенти вважають корисним малювати стрілки, щоб нагадати їм, як використовувати розподільну властивість. Тоді перший крок у прикладі 7.17 виглядатиме так:

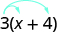
$$3 \cdot x + 3 \cdot 4$$

Приклад$\PageIndex{2}$:

Спрощення: 6 (5y + 1).

Рішення

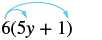
Розподілити.	$6\ крапка 5y + 6\ крапка 1$
Помножити.	$30 за рік + 6$$

Вправа$\PageIndex{3}$:

Спрощення: 9 (3y + 8).

Відповідь

27 років + 72

Вправа$\PageIndex{4}$:

Спрощення: 5 (5 Вт + 9).

Відповідь

25 Вт + 45

Властивість distributive може бути використана для спрощення виразів, які виглядають дещо відмінними від a (b + c). Ось дві інші форми.

Визначення: Розподільна власність

Якщо a, b, c є дійсними числами, то

$$a(b + c) = ab + ac$$Other forms$$a(b − c) = ab − ac$$$$(b + c)a = ba + ca$$

Приклад$\PageIndex{3}$:

Спрощення: 2 (x − 3).

Рішення

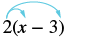
Розподілити.	$2\ крапка х 2\ крапка 3$
Помножити.	$2х - 6$$

Вправа$\PageIndex{5}$:

Спрощення: 7 (x − 6).

Відповідь

7х - 42

Вправа$\PageIndex{6}$:

Спрощення: 8 (x − 5).

Відповідь

8х - 40

Пам'ятаєте, як помножити дріб на ціле число? Ми повинні зробити це в наступних двох прикладах.

Приклад$\PageIndex{4}$:

Спростити:$\dfrac{3}{4}$ (n + 12).

Рішення

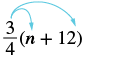
Розподілити.	$\ drac {3} {4}\ точка n +\ dfrac {3} {4}\ точка 12$$
Помножити.	$$\ дфрак {3} {4} n + 9$$

Вправа$\PageIndex{7}$:

Спростити:$\dfrac{2}{5}$ (р + 10).

Відповідь

$\frac{2}{5}p + 4$

Вправа$\PageIndex{8}$:

Спрощення:$\dfrac{3}{7}$ (u + 21).

Відповідь

$\frac{3}{7}u +9$

Приклад$\PageIndex{5}$:

Спростити:$8 \left(\dfrac{3}{8}x + \dfrac{1}{4}\right)$.

Рішення

Розподілити.	$8\ точка\ фрак {3} {8} х + 8\ точка\ drac {1} {4} $$
Помножити.	$3х + 2$$

Вправа$\PageIndex{9}$:

Спростити:$6 \left(\dfrac{5}{6}y + \dfrac{1}{2}\right)$.

Відповідь

5 років + 3

Вправа$\PageIndex{10}$:

Спростити:$12 \left(\dfrac{1}{3}n + \dfrac{3}{4}\right)$.

Відповідь

4м + 9

Використання Distributive Property, як показано в наступному прикладі, буде дуже корисно, коли ми вирішимо грошові додатки пізніше.

Приклад$\PageIndex{6}$:

Спрощення: 100 (0,3 + 0,25 кв).

Рішення

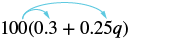
Розподілити.	$100 (0.3) + 100 (0.25кв) $
Помножити.	$30 + 25 к$$

Вправа$\PageIndex{11}$:

Спрощення: 100 (0,7 + 0,15р).

Відповідь

70 + 15р

Вправа$\PageIndex{12}$:

Спрощення: 100 (0,04 + 0,35д).

Відповідь

4 + 35д

У наступному прикладі ми помножимо на змінну. Ми повинні зробити це в наступному розділі.

Приклад$\PageIndex{7}$:

Спростити:$m(n − 4)$.

Рішення

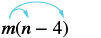
Розподілити.	$m\ точка n - м\ точка 4$$
Помножити.	$$млн - 4м$$

Зверніть увагу, що ми написали m • 4 як 4m. Ми можемо зробити це через Комутативну властивість множення. Коли термін є добутком числа та змінної, спочатку записуємо число.

Вправа$\PageIndex{13}$:

Спростити: r (s − 2).

Відповідь

рс - 2р

Вправа$\PageIndex{14}$:

Спростити: y (z − 8).

Відповідь

йз - 8г

У наступному прикладі буде використана форма «назад» розподільної властивості, (b + c) a = ba + ca.

Приклад$\PageIndex{8}$:

Спростити: (х + 8) п.

Рішення

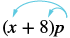
Розподілити.

$$пікселі+8п$$

Вправа$\PageIndex{15}$:

Спростити: (х + 2) р.

Відповідь

хр + 2р

Вправа$\PageIndex{16}$:

Спростити: (y + 4) q.

Відповідь

тк + 4кв

При розподілі негативного числа потрібно бути особливо обережним, щоб знаки були правильними.

Приклад$\PageIndex{9}$:

Спрощення: −2 (4y + 1).

Рішення

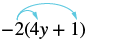
Розподілити.	$-2\ точка 4y + (-2)\ точка $1 $
Спростити.	$-8рік - 2$$

Вправа$\PageIndex{17}$:

Спрощення: −3 (6м+ 5).

Відповідь

-18м - 15

Вправа$\PageIndex{18}$:

Спрощення: −6 (8n + 11).

Відповідь

-48н - 66

Приклад$\PageIndex{10}$:

Спрощення: −11 (4 − 3a).

Рішення

Розподілити.	$-11\ точка 4 - (-1)\ крапка 3a$$
Помножити.	$-44 - (-33а) $$
Спростити.	$-44 + 33а$$

Ви також можете записати результат як 33a − 44. Знаєте чому?

Вправа$\PageIndex{19}$:

Спрощення: −5 (2 − 3a).

Відповідь

-10 + 15а

Вправа$\PageIndex{20}$:

Спрощення: −7 (8 − 15 років).

Відповідь

-56 + 105 г

У наступному прикладі ми покажемо, як використовувати властивість Distributive, щоб знайти протилежне виразу. Пам'ятайте, −a = −1 • a.

Приклад$\PageIndex{11}$:

Спростити: − (y + 5).

Рішення

Множення на −1 призводить до протилежного.	$-1 (у + 5) $$
Розподілити.	$-1\ крапка у + (-1)\ точка 5$$
Спростити.	$$-у + (-5)$$
Спростити.	$$-у -5$$

Вправа$\PageIndex{21}$:

Спрощення: − (z − 11).

Відповідь

-з + 11

Вправа$\PageIndex{22}$:

Спростити: − (x − 4).

Відповідь

-х + 4

Іноді нам потрібно використовувати розподільну властивість як частину порядку операцій. Почніть з погляду на дужки. Якщо вираз всередині дужок не можна спростити, наступним кроком буде множення за допомогою властивості distributive, яка видаляє дужки. Наступні два приклади проілюструють це.

Приклад$\PageIndex{12}$:

Спрощення: 8 − 2 (x + 3).

Рішення

Розподілити.	$8 - 2\ крапка х - 2\ крапка 3$$
Помножити.	$8 - 2x - 6$$
Поєднуйте подібні терміни.	$-2х + 2$$

Вправа$\PageIndex{23}$:

Спрощення: 9 − 3 (x + 2).

Відповідь

-3х+ 3

Вправа$\PageIndex{24}$:

Спрощення: 7x − 5 (x + 4).

Відповідь

2х - 20

Приклад$\PageIndex{13}$:

Спрощення: 4 (x − 8) − (x + 3).

Рішення

Розподілити.	$4x - 32 - х - 3$
Поєднуйте подібні терміни.	$3x - 35$

Вправа$\PageIndex{25}$:

Спрощення: 6 (x − 9) − (x + 12).

Відповідь

5х - 66

Вправа$\PageIndex{26}$:

Спрощення: 8 (x − 1) − (x + 5).

Відповідь

7х - 13

Оцінити вирази за допомогою розподільної властивості

Деяким студентам потрібно переконатися, що розподільна власність завжди працює. У наведених нижче прикладах ми будемо практикувати оцінку деяких виразів з попередніх прикладів; в частині (a) ми будемо оцінювати форму дужками, а в частині (b) ми оцінимо форму, яку ми отримали після розподілу. Якщо правильно оцінити обидва вирази, це покаже, що вони дійсно рівні.

Приклад$\PageIndex{14}$:

Коли у = 10 оцінюють: (а) 6 (5й + 1) (б) 6 • 5у + 6 • 1.

Рішення

(а) 6 (5й + 1)

$\textcolor{red}{10}$Замінник у.	$6 (5\ крапка\ колір тексту {червоний} {10} + 1) $$
Спрощення в дужках.	$6 (51) $$
Помножити.	$306 $$

(б) 6 • 5 років + 6 • 1

$\textcolor{red}{10}$Замінник у.	$6\ крапка 5\ крапка\ колір тексту {червоний} {10} + 6\ крапка 1$$
Спростити.	$300 + 6$$
Додати.	$306 $$

Зверніть увагу, відповіді однакові. Коли у = 10, 6 (5у + 1) = 6 • 5у + 6 • 1. Спробуйте самі для іншого значення у.

Вправа$\PageIndex{27}$:

Оцініть, коли w = 3: (а) 5 (5w + 9) (b) 5 • 5w + 5 • 9.

Відповідь на

$120$

Відповідь б

$120$

Вправа$\PageIndex{28}$:

Оцініть, коли у = 2: (а) 9 (3y + 8) (b) 9 • 3y + 9 • 8.

Відповідь на

$126$

Відповідь б

$126$

Приклад$\PageIndex{15}$:

Коли y = 3, оцініть (a) −2 (4y + 1) (b) −2 • 4y + (−2) • 1.

Рішення

(a) −2 (4y + 1)

$\textcolor{red}{3}$Замінник у.	$-2 (4\ крапка\ колір тексту {червоний} {3} + 1) $$
Спрощення в дужках.	$-2 (13) $$
Помножити.	$-26$$

(б) −2 • 4й + (−2) • 1

$\textcolor{red}{3}$Замінник у.	$-2\ крапка 4\ крапка\ колір тексту {червоний} {3} + (-2)\ крапка 1$$
Помножити.	$-24 - 2$$
Відніміть.	$-26$$
Відповіді ті ж, коли y = 3.	$-2 (4й + 1) = -8у - 2$$

Вправа$\PageIndex{29}$:

Оцінити, коли n = −2: (a) −6 (8n + 11) (b) −6 • 8n + (−6) • 11.

Відповідь на

$30$

Відповідь б

$30$

Вправа$\PageIndex{30}$:

Оцінити, коли m = −1: (a) −3 (6m + 5) (b) −3 • 6m + (−3) • 5.

Відповідь на

$3$

Відповідь б

$3$

Приклад$\PageIndex{16}$:

Коли y = 35, оцініть (a) − (y + 5) та (b) −y − 5, щоб показати, що − (y + 5) = −y − 5.

Рішення

(а) − (у + 5)

$\textcolor{red}{35}$Замінник у.	$$- (\ колір тексту {червоний} {35} + 5)$$
Додайте в дужках.	$$- (40)$$
Спростити.	$-40$$

(b) −y − 5

$\textcolor{red}{35}$Замінник у.	$$-\ колір тексту {червоний} {35} - 5$$
Спростити.	$-40$$
Відповіді однакові, коли y = 35, демонструючи, що	$- (у + 5) = -у - 5$$

Вправа$\PageIndex{31}$:

Оцініть, коли x = 36: (a) − (x − 4) (b) −x + 4, щоб показати, що − (x − 4) = − x + 4.

Відповідь на

$-32$

Відповідь б

$-32$

Вправа$\PageIndex{32}$:

Оцініть, коли z = 55: (a) − (z − 10) (b) −z + 10, щоб показати, що − (z − 10) = − z + 10.

Відповідь на

$-45$

Відповідь б

$-45$

ДОСТУП ДО ДОДАТКОВИХ ОНЛАЙН-РЕСУРСІВ

Розподіл моделі

Розподільна власність

Практика робить досконалим

Спрощення виразів за допомогою властивості розподілу

У наступних вправах спростіть використання розподільного властивості.

90. 4 (х + 8)
91. 3 (а + 9)
92. 8 (4 роки + 9)
93. 9 (3 Вт + 7)
94. 6 (c − 13)
95. 7 (г − 13)
96. 7 (3p − 8)
97. 5 (7u − 4)
98. $\dfrac{1}{2}$(n + 8)
99. $\dfrac{1}{3}$(до +9)
100. $\dfrac{1}{4}$(3 кв + 12)
101. $\dfrac{1}{5}$(4м + 20)
102. $9 \left(\dfrac{5}{9} y − \dfrac{1}{3}\right)$
103. $10 \left(\dfrac{3}{10} x − \dfrac{2}{5}\right)$
104. $12 \left(\dfrac{1}{4} + \dfrac{2}{3} r\right)$
105. $12 \left(\dfrac{1}{6} + \dfrac{3}{4} s\right)$
106. r (s − 18)
107. u (v − 10)
108. (у + 4) р
109. (а + 7) х
110. −2 (у + 13)
111. −3 (а + 11)
112. −7 (4р + 1)
113. −9 (9а + 4)
114. −3 (x − 6)
115. −4 (q − 7)
116. −9 (3а − 7)
117. −6 (7x − 8)
118. − (r + 7)
119. − (q + 11)
120. − (3x − 7)
121. − (5p − 4)
122. 5 + 9 (n − 6)
123. 12 + 8 (u − 1)
124. 16 − 3 (у + 8)
125. 18 − 4 (х + 2)
126. 4 − 11 (3с − 2)
127. 9 − 6 (7n − 5)
128. 22 − (а + 3)
129. 8 − (r − 7)
130. −12 − (u + 10)
131. −4 − (c − 10)
132. (5м − 3) − (m + 7)
133. (4y − 1) − (y − 2)
134. 5 (2н + 9) + 12 (n − 3)
135. 9 (5u + 8) + 2 (u − 6)
136. 9 (8x − 3) − (−2)
137. 4 (6x − 1) − (−8)
138. 14 (c − 1) − 8 (c − 6)
139. 11 (n − 7) − 5 (n − 1)
140. 6 (7 років + 8) − (30 років − 15)
141. 7 (3n + 9) − (4n − 13)

Оцінити вирази за допомогою розподільної властивості

У наступних вправах оцініть обидва вирази для заданого значення.

142. Якщо v = −2, оцініть
     1. 6 (4 в + 7)
     2. 6 · 4 В + 6 · 7
143. Якщо u = −1, оцініть
     1. 8 (5у + 12)
     2. 8 · 5 Вт + 8 · 12
144. Якщо n =$\dfrac{2}{3}$, оцініть
     1. $3 \left(n + \dfrac{5}{6}\right)$
     2. 3 • n + 3 •$\dfrac{5}{6}$
145. Якщо y = 3 4, оцініть
     1. 4 y + 3 8
     2. 4 • у + 4 •$\dfrac{3}{8}$
146. Якщо y =$\dfrac{7}{12}$, оцініть
     1. −3 (4й + 15)
     2. 3 • 4 г + (−3) • 15
147. Якщо p =$\dfrac{23}{30}$, оцініть
     1. −6 (5п + 11)
     2. −6 • 5п + (−6) • 11
148. Якщо m = 0,4, оцініть
     1. −10 (3м − 0.9)
     2. −10 • 3м − (−10) (0.9)
149. Якщо n = 0,75, оцініть
     1. −100 (5н + 1,5)
     2. −100 • 5н + (−100) (1.5)
150. Якщо y = −25, оцініть
     1. − (y − 25)
     2. −у + 25
151. Якщо w = −80, оцініть
     1. − (ш − 80)
     2. −ш + 80
152. Якщо р = 0,19, оцініть
     1. − (p + 0.72)
     2. −p − 0,72
153. Якщо q = 0,55, оцініть
     1. − (q + 0.48)
     2. −q − 0,48

Щоденна математика

154. Купуючи справу Джо може купити свій улюблений чай з льодом в цілодобовому магазині за $1,99 за пляшку. У продуктовому магазині він може купити футляр з 12 пляшок за $23,88.
     1. Використовуйте розподільну властивість, щоб знайти вартість 12 пляшок, придбаних індивідуально в магазині. (Підказка: зверніть увагу, що $1,99 становить $2 − $0,01.)
     2. Чи вигідна пропозиція купувати крижаний чай у продуктовому магазині на випадок?
155. Multi-pack купити шампунь Adele's продається за $3,97 за пляшку в аптеці. У складському магазині такий же шампунь продається як 3-пачка за $10,49.
     1. Покажіть, як можна використовувати розподільну властивість, щоб знайти вартість 3 флаконів, придбаних індивідуально в аптеці.
     2. Скільки б Адель заощадив, купивши 3-упаковку в складському магазині?

Письмові вправи

156. Спростіть$8 \left(x − \dfrac{1}{4}\right)$ використання властивості distributive і пояснити кожен крок.
157. Поясніть, як можна помножити 4 ($5,97) без паперу чи калькулятора, подумавши про $5,97 як 6 − 0,03, а потім використовуючи розподільну властивість.

Самостійна перевірка

(а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

(б) Що цей контрольний список розповідає вам про ваше володіння цим розділом? Які кроки ви зробите для вдосконалення?

Автори та атрибуція

• Template:ContribOpenStaxPreAlgebra