5.1: Тригонометричні функції

Тригонометрія (від грецьких слів означає трикутник-міра) - це галузь математики, що займається обчисленням невідомих сторін і кутів трикутників. Наприклад, на малюнку$\PageIndex{1}$, ми можемо захотіти виміряти висоту дерева, фактично не піднімаючись на дерево. Методи тригонометрії дозволять нам це зробити.

Малюнок$\PageIndex{1}$: Тригонометрія дозволить нам виміряти висоту дерева, фактично не піднімаючись на дерево,

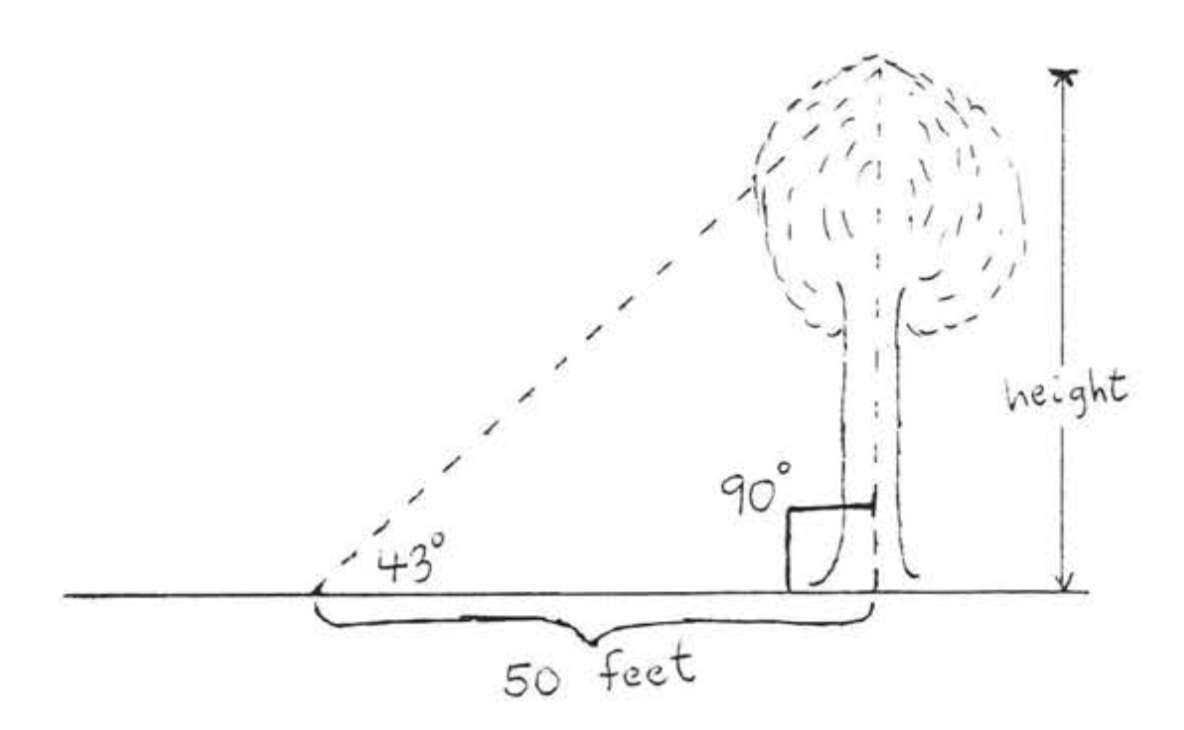
У цій книзі ми розглянемо якраз тригонометрію прямокутного трикутника. У більш просунутих курсах тригонометрія має справу з іншими видами трикутників, а також. Однак тут наведені нижче визначення стосуються лише правильних трикутників.

У прямокутному$ABC$ трикутнику фігури$\PageIndex{2}$,$AC$ називається ніжкою, прилеглою до$\angle A$. «Сусідні» означає «поруч». $BC$називається ніжкою протилежної$\angle A$. «Навпроти» тут означає «найвіддаленіший від».

Малюнок$\PageIndex{2}$: Прямий трикутник$ABC$.

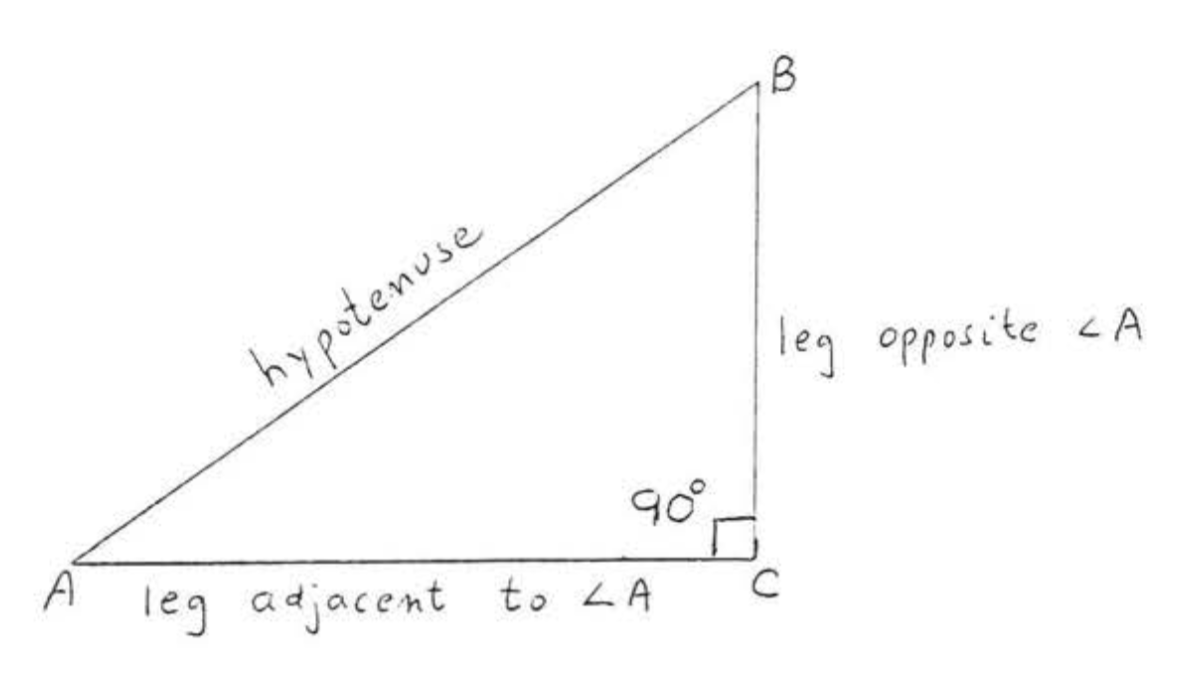
Ми визначаємо синус, косинус і тангенс гострого кута$A$ в прямокутному трикутнику наступним чином:

$\begin{array} {lcl} {\text{sine } A = \dfrac{\text{leg opposite } \angle A}{\text{hypotenuse}}} & \ \ \ & {(\sin A = \dfrac{\text{opp}}{\text{hyp}})} \\ {\text{cosine } A = \dfrac{\text{leg adjacent to } \angle A}{\text{hypotenuse}}} & \ \ \ & {(\cos A = \dfrac{\text{adj}}{\text{hyp}})} \\ {\text{tangent } A = \dfrac{\text{leg opposite } \angle A}{\text{leg adjacent to } \angle A}} & \ \ \ & {(\tan A = \dfrac{\text{opp}}{\text{adj}})} \end{array}$

Синус, косинус і тангенс називаються тригонометричними функціями.

Приклад$\PageIndex{1}$

Знайдіть синус, косинус і тангенс$\angle A$:

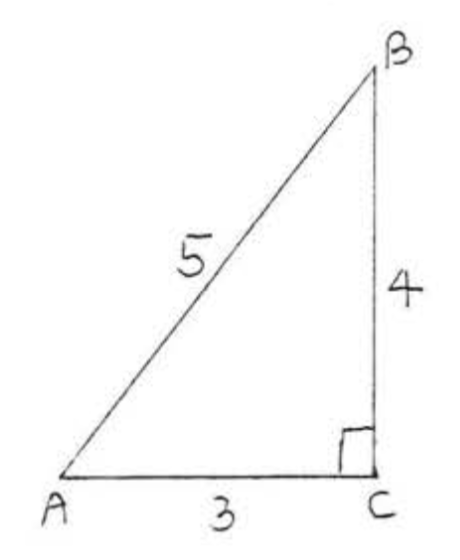
Рішення

нога прилегла до$\angle A = 3$.

нога протилежна$\angle A = 4$.

гіпотенуза = 5.

$\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{4}{5}$. $\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{3}{5}$. $\tan A = \dfrac{\text{opp}}{\text{adj}} = \dfrac{4}{3}$.

Відповідь:$\sin A = \dfrac{4}{5}$,$\cos A = \dfrac{3}{5}$,$\tan A = \dfrac{4}{3}$.

Приклад$\PageIndex{2}$

Знайдіть синус, косинус і тангенс$\angle B$:

Рішення

нога прилегла до$\angle B = 4$.

нога протилежна$\angle B = 3$.

гіпотенуза = 5.

$\sin B = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{3}{5}$. $\cos B = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{4}{5}$. $\tan B = \dfrac{\text{opp}}{\text{adj}} = \dfrac{3}{4}$.

Відповідь:$\sin B = \dfrac{3}{5}$,$\cos B = \dfrac{4}{5}$,$\tan B = \dfrac{3}{4}$.

Визначення синуса, косинуса і тангенса повинні бути запам'ятовані, Це може бути корисно, щоб згадати мнемоніку «SOHCAHTOA:»

Приклад$\PageIndex{3}$

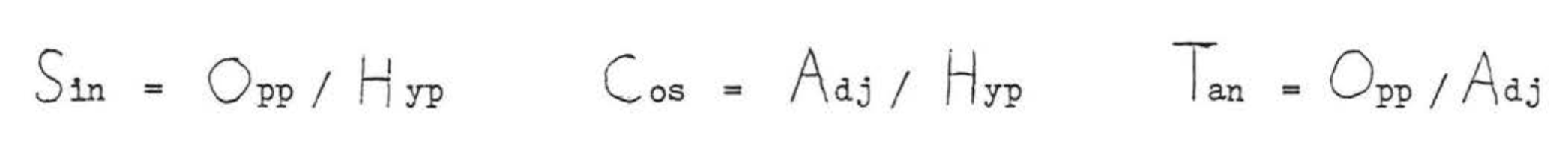
Знайти$\sin A$$\cos A$, і$\tan A$:

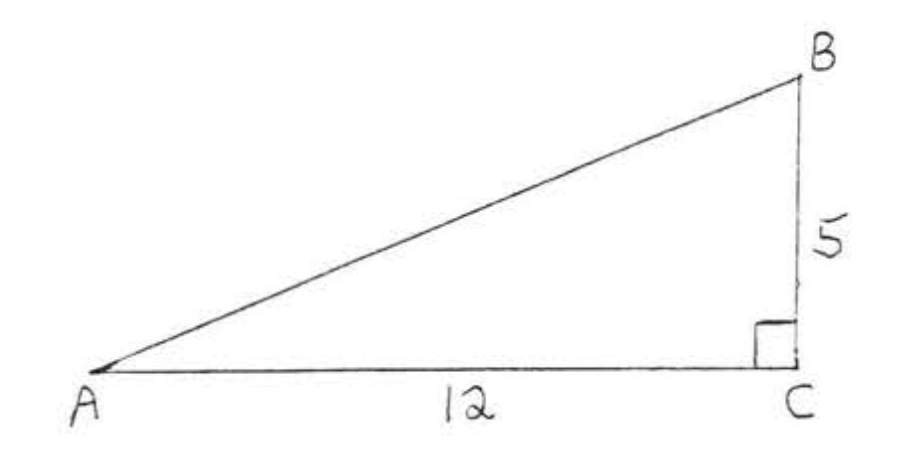
Рішення

Щоб знайти гіпотенузу, скористаємося теоремою Піфагора:

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {5^2 + 12^2} & = & {\text{hyp}^2} \\ {25 + 144} & = & {\text{hyp}^2} \\ {169} & = & {\text{hyp}^2} \\ {13} & = & {\text{hyp}} \end{array}$

$\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{5}{13}$. $\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{12}{13}$. $\tan A = \dfrac{\text{opp}}{\text{adj}} = \dfrac{5}{12}$.

Відповідь:$\sin A = \dfrac{5}{13}$,$\cos A = \dfrac{12}{13}$,$\tan A = \dfrac{5}{12}$.

Приклад$\PageIndex{4}$

Знайти$\sin A$$\cos A$, і$\tan A$:

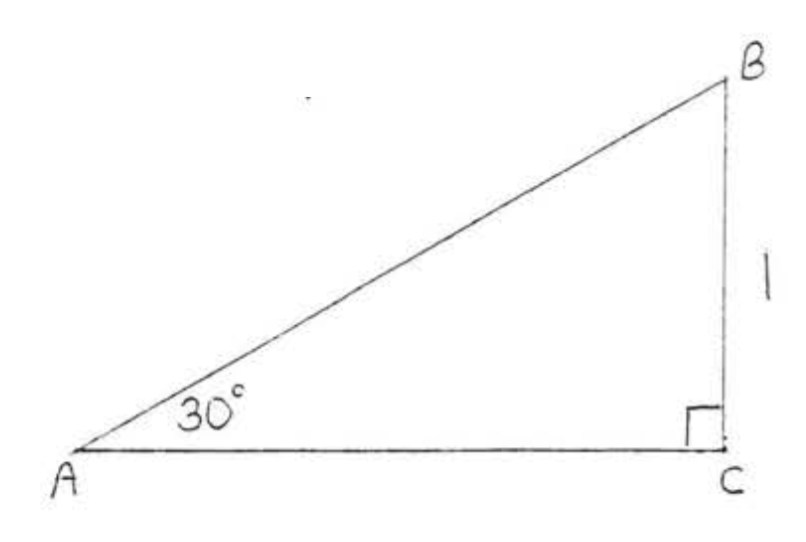
Рішення

$\triangle ABC$це$30^{\circ}-60^{\circ}-90^{\circ}$ трикутник так по теоремі 4.5.1, Розділ 4.5,$AB = \text{hyp} = 2s = 2(1) = 2$ і$AC = L = s\sqrt{3} = (1) \sqrt{3} = \sqrt{3}$.

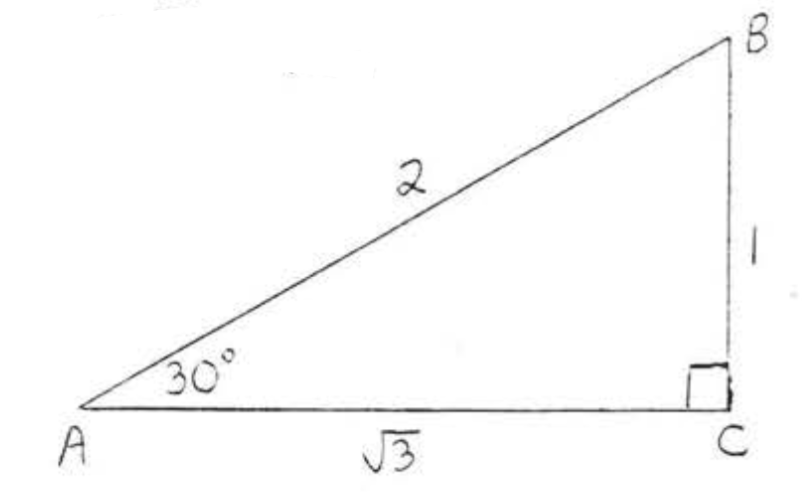
$\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{1}{2}$,$\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{\sqrt{3}}{2}$,

$\tan A = \dfrac{\text{opp}}{\text{adj}} = \dfrac{1}{\sqrt{3}} = \dfrac{1}{\sqrt{3}} \dfrac{\sqrt{3}}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}$.

Відповідь:$\sin A = \dfrac{1}{2}$,$\cos A = \dfrac{\sqrt{3}}{2}$,$\tan A = \dfrac{\sqrt{3}}{3}$.

Приклад$\PageIndex{5}$

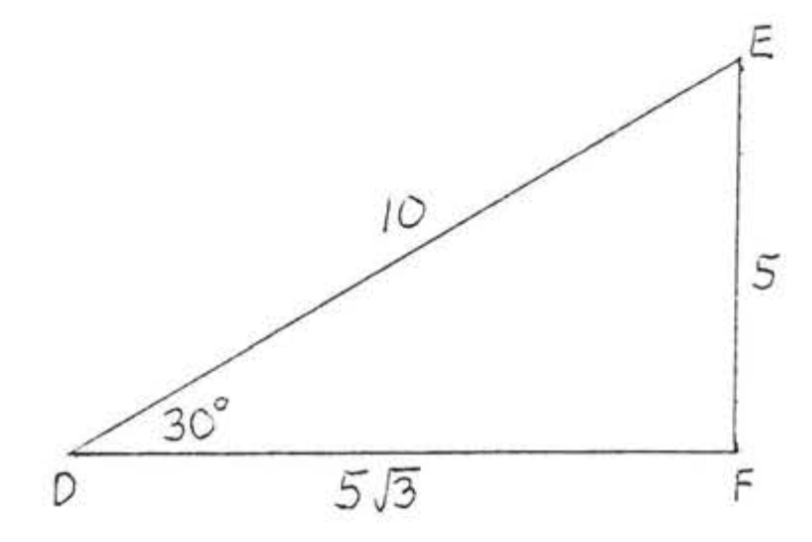
Знайти$\sin D, \cos D$, і$\tan D$:

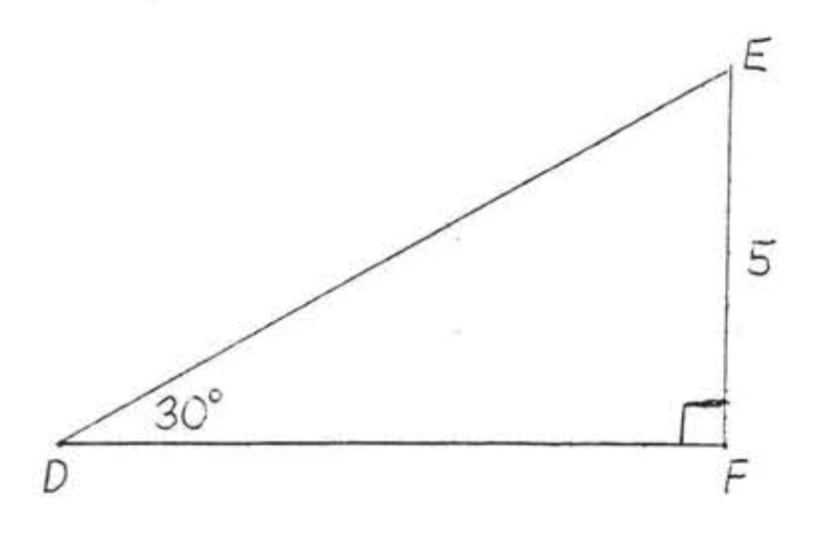
Рішення

Знову використовуючи теорему 4.5.1, розділ 4.5,$DE = \text{hyp} = 2s = 2(5) = 10$ і$DF = L = s\sqrt{3} = 5\sqrt{3}$.

$\sin D = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{5}{10} = \dfrac{1}{2}$,$\cos D = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{5\sqrt{3}}{10} = \dfrac{\sqrt{3}}{2}$,$\tan D = \dfrac{\text{opp}}{\text{adj}} = \dfrac{5}{5\sqrt{3}} = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}$.

Відповідь:$\sin D = \dfrac{1}{2}$,$\cos D = \dfrac{\sqrt{3}}{2}$,$\tan D = \dfrac{\sqrt{3}}{3}$.

Зверніть увагу, що відповіді на Приклад$\PageIndex{4}$ до Прикладу$\PageIndex{5}$ були однаковими. Це тому, що$\angle A = \angle D = 30^{\circ}$. Значення тригонометричних функцій для всіх$30^{\circ}$ кутів будуть однаковими, Причина в тому, що всі правильні трикутники з$30^{\circ}$ кутом схожі. Тому їх сторони пропорційні, а тригонометричні співвідношення рівні. Що тримає для$30^{\circ}$ кутів тримає і для інших гострих кутів, а також. Ми стверджуємо це в наступній теоремі:

Теорема$\PageIndex{1}$

Значення тригонометричних функцій для рівних кутів однакові.

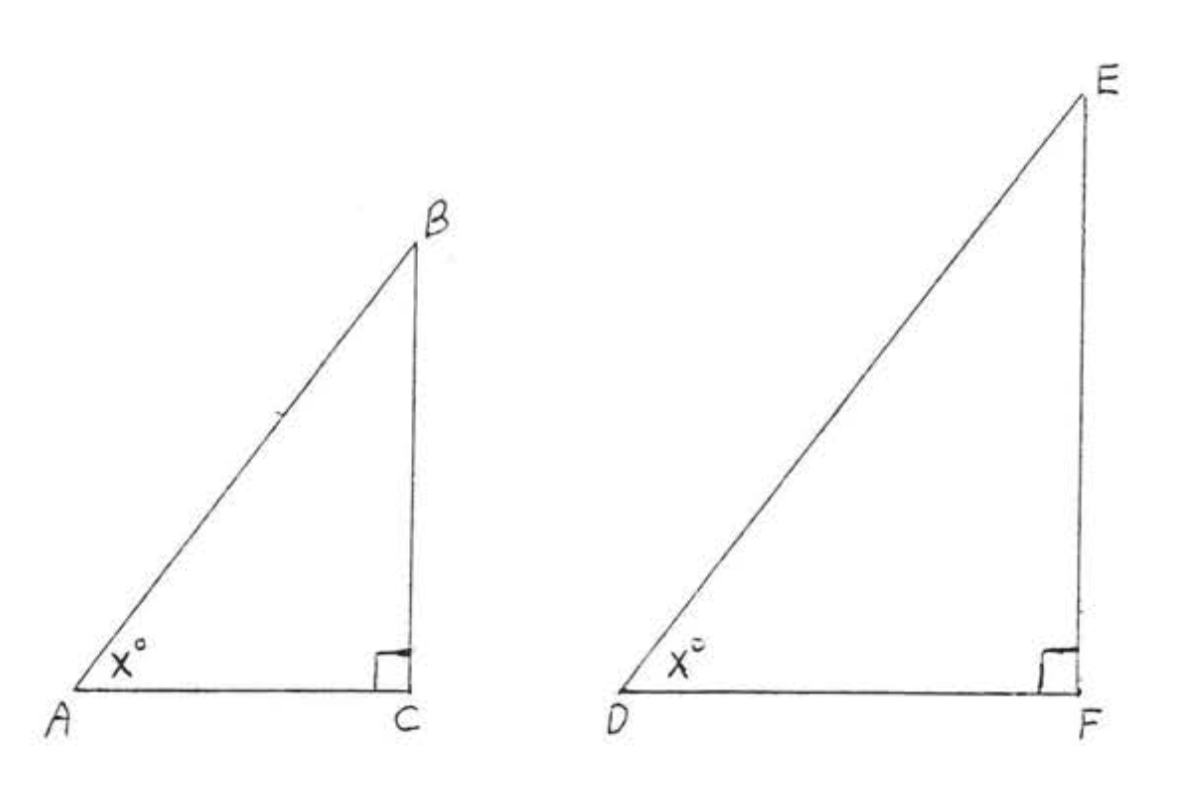
На малюнку$\PageIndex{3}$, якщо$\angle A = \angle D = x^{\circ}$ тоді$\sin A = \sin D$$\cos A = \cos D$, і$\tan A = \tan D$.

Доказ

$\angle A = \angle D = x^{\circ}$і$\angle C = \angle F = 90^{\circ}$ так$\triangle ABC \cong \triangle DEF$ по$AA = AA$. Тому,

$\dfrac{BC}{EF} = \dfrac{AB}{DE}$$\dfrac{AC}{DF} = \dfrac{AB}{DE}$і$\dfrac{BC}{EF} = \dfrac{AC}{DF}$.

За теоремою 4.1.2, розділ 4.1, ми можемо обмінюватися засобами кожної пропорції:

$\dfrac{BC}{AB} = \dfrac{EF}{DE}$$\dfrac{AC}{AB} = \dfrac{DF}{DE}$і$\dfrac{BC}{AC} = \dfrac{EF}{DF}$.

Ці пропорції просто стверджують, що

$\sin A = \sin D$, І$\cos A = \cos D$, і$\tan A = \tan D$.

Теорема$\PageIndex{1}$ говорить нам, що тригонометричні функції залежать не від конкретного обраного трикутника, а лише від кількості градусів в куті. Якщо ми хочемо знайти тригонометричні значення кута, ми можемо вибрати будь-який прямокутний трикутник, що містить кут, який зручно використовувати.

Приклад$\PageIndex{6}$

Якщо$\sin A = \dfrac{12}{13}$ знайти$\cos A$ і$\tan A$.

Рішення

Якщо$\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{12}{13}$ тоді існує прямокутний трикутник,$ABC$ що містить$\angle A$ з катетом протилежним$\angle = 12$ і гіпотенузою = 13 (див. Рис.$\PageIndex{4}$).

Малюнок$\PageIndex{4}$:$\triangle ABC$ з катетом протилежним$\angle A = 12$ і гіпотенузою = 13.

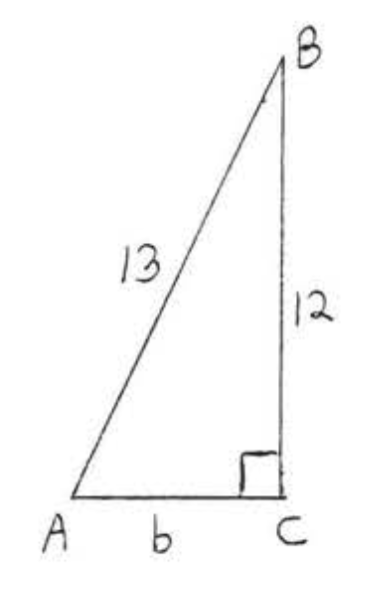
Нехай$b =$ нога прилягає до$\angle A$.

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {b^2 + 12^2} & = & {13^2} \\ {b^2 + 144} & = & {169} \\ {-144} & \ & {-144} \\ {b^2} & = & {25} \\ {b} & = & {5} \end{array}$

$\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{5}{13}$,$\tan A = \dfrac{\text{opp}}{\text{adj}} = \dfrac{12}{5}$.

Відповідь:$\cos A = \dfrac{5}{13}$,$\tan A = \dfrac{12}{5}$.

Приклад$\PageIndex{7}$

Якщо$\tan A = 2$ знайти$\sin A$ і$\cos A$.

Рішення

$\tan A = \dfrac{\text{opp}}{\text{adj}} = 2 = \dfrac{2}{1}$. $\triangle ABC$Дозволяти бути таким, що$a=$ нога протилежна$\angle A = 2$ і$b =$ нога прилегла до$\angle A = 1$. Див$\PageIndex{5}$. Малюнок.

Малюнок$\PageIndex{5}$:$\triangle ABC$ з$a = 2$ і$b = 1$.

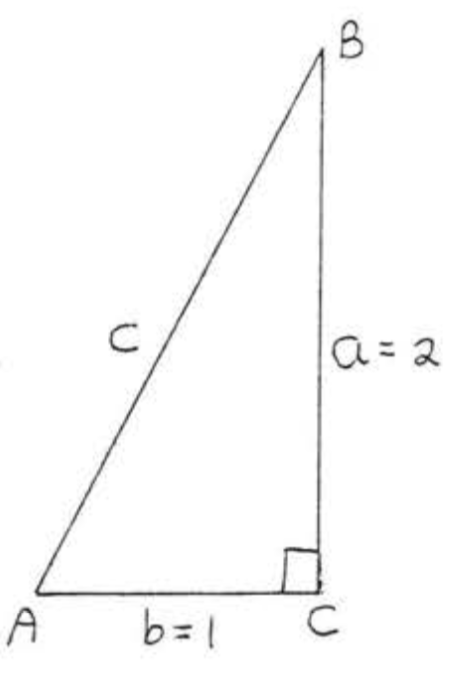
$\begin{array} {rcl} {a^2 + b^2} & = & {c^2} \\ {2^2 + 1^2} & = & {c^2} \\ {4 + 1} & = & {c^2} \\ {5} & = & {c^2} \\ {\sqrt{5}} & = & {c} \end{array}$

$\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{2}{\sqrt{5}} = \dfrac{2}{\sqrt{5}} \dfrac{\sqrt{5}}{\sqrt{5}} = \dfrac{2\sqrt{5}}{5}$.

$\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{1}{\sqrt{5}} = \dfrac{1}{\sqrt{5}} \dfrac{\sqrt{5}}{\sqrt{5}} = \dfrac{\sqrt{5}}{5}$.

Відповідь:$\sin A = \dfrac{2\sqrt{5}}{5}$,$\cos A = \dfrac{\sqrt{5}}{5}$.

Проблеми

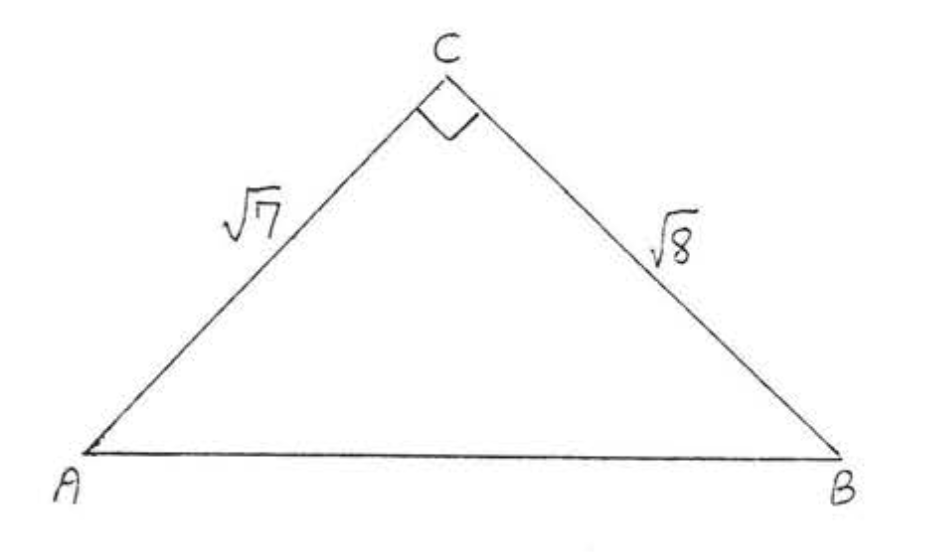
1 - 14. Знайти$\sin A, \cos A, \tan A, \sin B, \cos B$, і$\tan B$:

1.

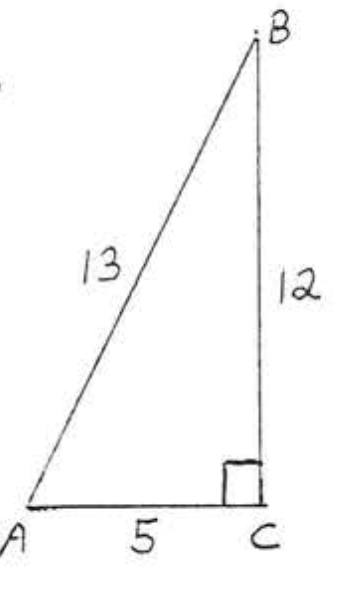
2.

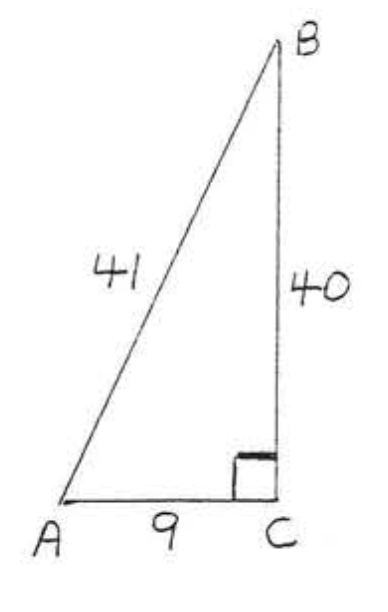
3.

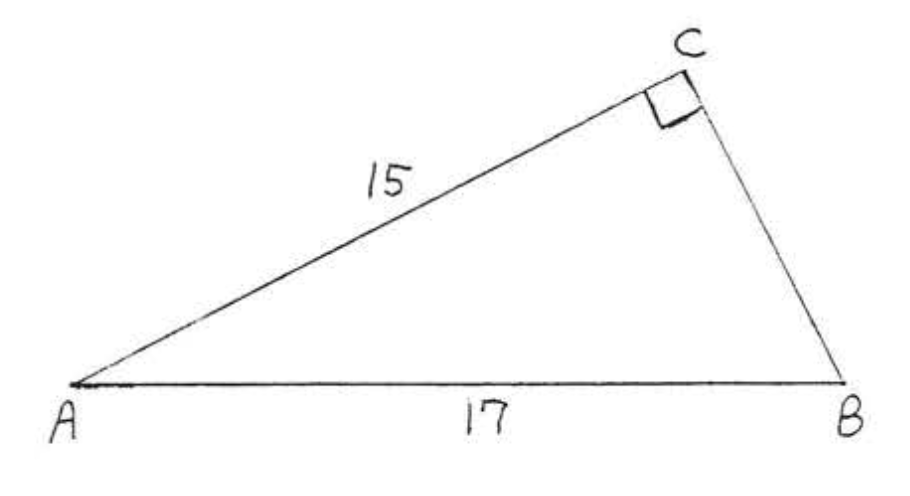
4.

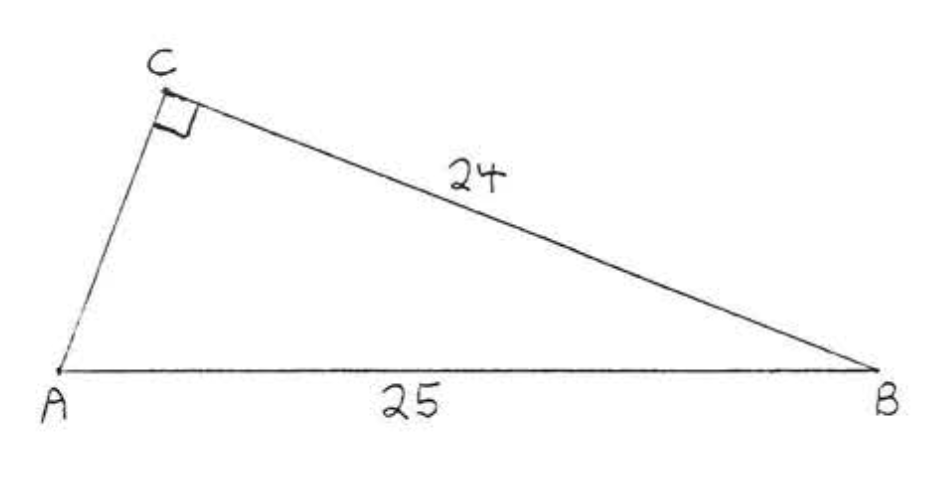
5.

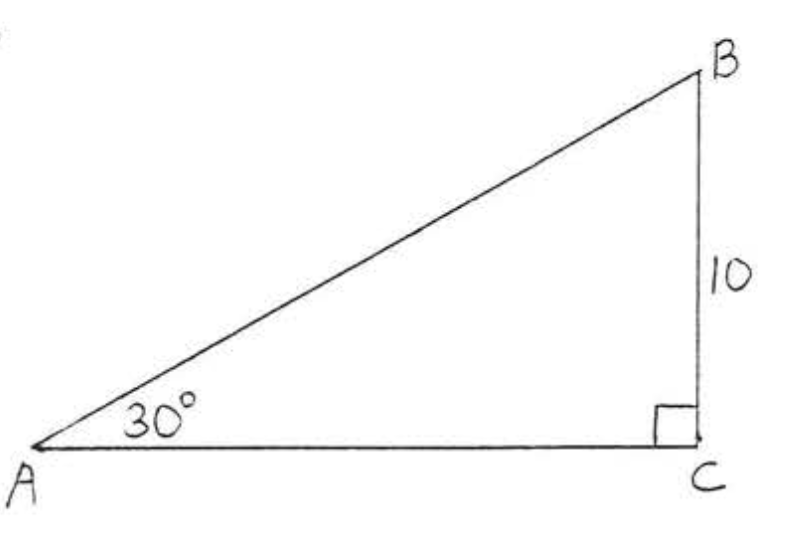
6.

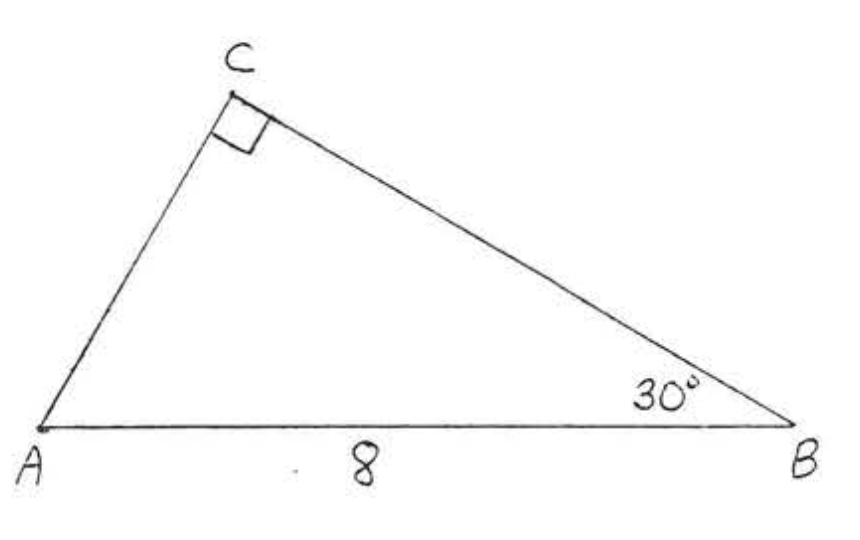
7.

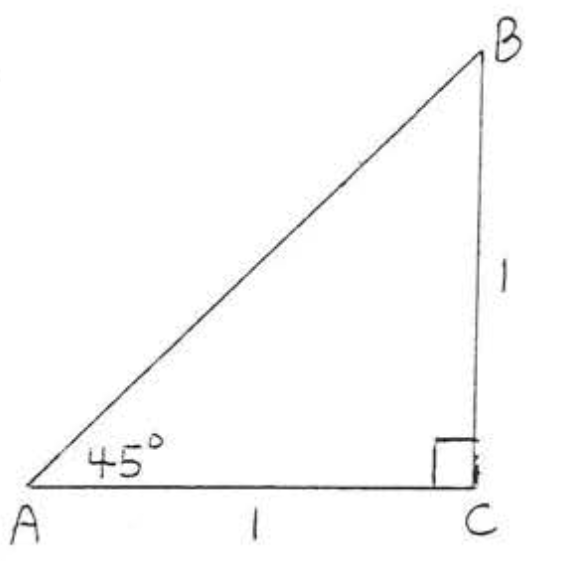
8.

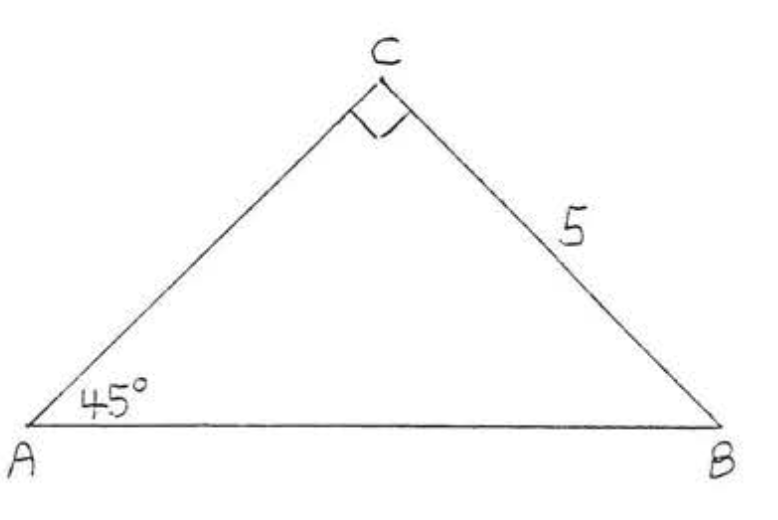
9.

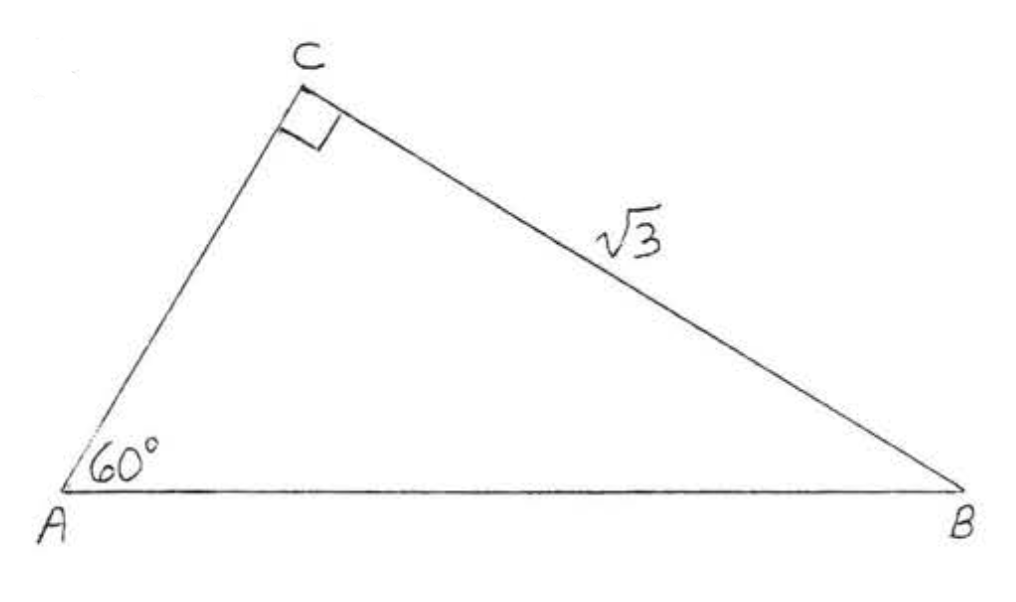
10.

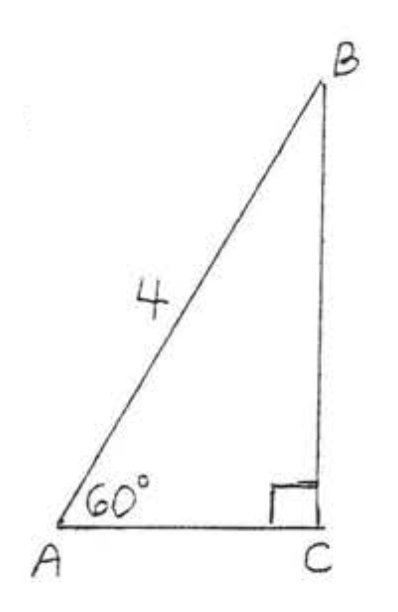
11.

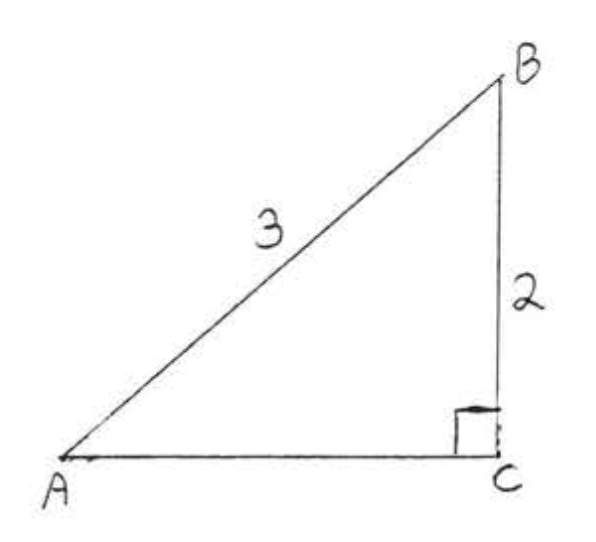
12.

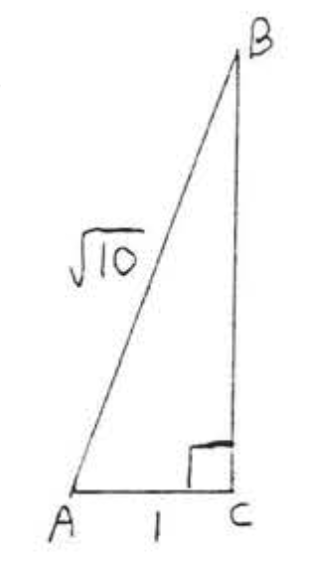
13.

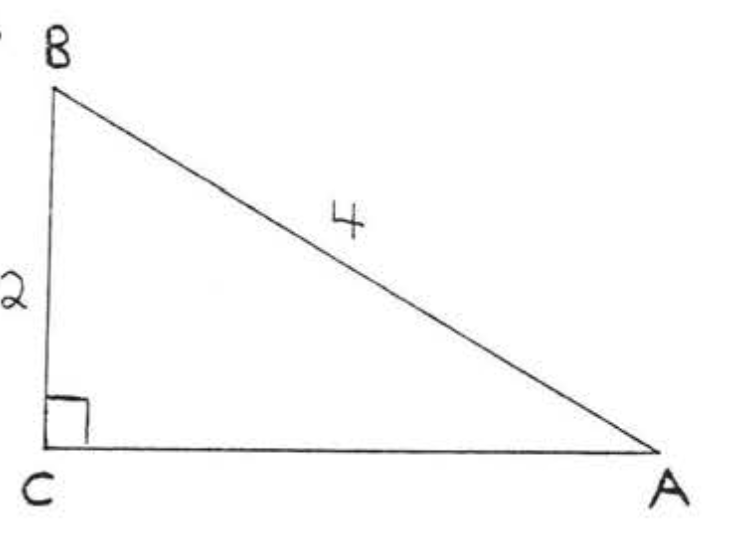
14.

15. Якщо$\sin A = \dfrac{4}{5}$ знайти$\cos A$ і$\tan A$.

16. Якщо$\sin A = \dfrac{\sqrt{2}}{2}$ знайти$\cos A$ і$\tan A$.

17. Якщо$\cos A = \dfrac{\sqrt{3}}{2}$ знайти$\sin A$ і$\tan A$.

18. Якщо$\cos A = \dfrac{1}{3}$ знайти$\sin A$ і$\tan A$.

19. Якщо$\tan A = 3$ знайти$\sin A$ і$\cos A$.

20. Якщо$\tan A = 1$ знайти$\sin A$ і$\cos A$.