4.3: Ізоселі трикутники

Last updated
Save as PDF

Page ID: 59142

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Трикутник з двома рівними сторонами називається рівнобедреним; решта - підставою.

Теорема$\PageIndex{1}$

Припустимо,$\triangle ABC$ це рівнобедрений трикутник з підставою$[AB]$. Тоді

$\measuredangle ABC \equiv - \measuredangle BAC.$

Більше того, зворотне утримує, якщо$\triangle ABC$ є невиродженим.

Наступним доказом є Паппус Олександрійський.

Доказ

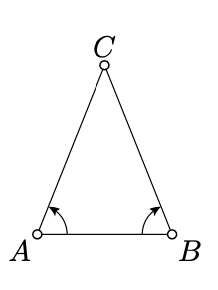
$2021-02-03 пнг$

Зауважте, що

$CA = CB$,$CB = CA$,$\measuredangle ACB \equiv -\measuredangle BCA$.

За аксіомою IV

$\triangle CAB \cong \triangle CBA.$

Застосовуючи теорему про знаки кутів трикутників (Теорема 3.3.1) І знову Аксіома IV, отримаємо, що

$\measuredangle BAC \equiv -\measuredangle ABC.$

Щоб довести зворотне, ми припускаємо, що$\measuredangle CAB \equiv - \measuredangle CBA$. За умовою ASA (теорема 4.2.1),$\triangle CAB \cong \triangle CBA$. Тому,$CA = CB$.

Трикутник з трьома рівними сторонами називається рівностороннім.

Вправа$\PageIndex{1}$

$\triangle ABC$Дозволяти рівносторонній трикутник. Покажіть, що

$\measuredangle ABC = \measuredangle BCA = \measuredangle CAB.$

Підказка: Застосовуйте теорему 4.3.1 двічі