37.1: Нерівності у написанні та графіках

Last updated
Save as PDF

Page ID: 882

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Урок

Давайте напишемо нерівності.

Вправа$\PageIndex{1}$: Estimate Heights of People

Ось картинка чоловіка.

Назвіть число, в ногах, яке явно занадто високо для зросту цієї людини.
Назвіть число, в футах, що явно занадто низько для його зростання.
Складіть оцінку його зростання.

Пауза тут для обговорення класу.

Ось фотографія того ж чоловіка, що стоїть поруч з дитиною.

Якщо фактичний зріст чоловіка становить 5 футів 10 дюймів, що ви можете сказати про зріст дитини на цій картині?

Будьте готові пояснити свої міркування.

Вправа$\PageIndex{2}$: Stories about 9

Перетягніть зелену та червону відкриті точки над синіми точками. Зіставте кожну історію з цифровою лінією та описом.
Подумайте про те, як би ви представляли кожен набір чисел твердженням про нерівність, поговоріть про це зі своїм партнером і будьте готові обговорити свої ідеї з класом. Потім запишіть свої остаточні рішення про відповідність тут.
- Рибальський човен може вмістити менше 9 осіб. Скільки людей ($x$) може вмістити?
  - Опис або список:
  - Номер рядка: $clipboard_e14f154ebcccde2c7ca5802f676ba1ec9.png$
    Малюнок$\PageIndex{3}$
  - Нерівність:
- Лін потребує більше 9 унцій вершкового масла, щоб зробити печиво для своєї партії. Скільки унцій вершкового масла ($x$) було б достатньо?
  - Опис або список:
  - Номер рядка: $clipboard_e14f154ebcccde2c7ca5802f676ba1ec9.png$
    Малюнок$\PageIndex{4}$
  - Нерівність:
- Маг буде виконувати свої магічні трюки тільки в тому випадку, якщо в аудиторії не менше 9 осіб. За скільки людей ($x$) вона буде виконувати свої магічні трюки?
  - Опис або список:
  - Номер рядка: $clipboard_e14f154ebcccde2c7ca5802f676ba1ec9.png$
    Малюнок$\PageIndex{5}$
  - Нерівність:
- Харчова шкала може вимірювати до 9 кілограмів ваги. Які ваги ($x$) може вимірювати шкала?
  - Опис або список:
  - Номер рядка: $clipboard_e14f154ebcccde2c7ca5802f676ba1ec9.png$
    Малюнок$\PageIndex{6}$
  - Нерівність:

Вправа$\PageIndex{3}$: How High and How Loc Can it Be?

Ось картинка людини і баскетбольне кільце. Виходячи з картини, які, на вашу думку, є розумними оцінками максимальної і мінімальної висоти баскетбольного кільця?

Заповніть перший бланк у кожному реченні оцінкою, а другий бланк «вище» або «коротше».

Я оцінюю мінімальну висоту баскетбольного кільця, щоб бути _________ футів; це означає, що обруч не може бути _____________ ніж ця висота.
Я оцінюю максимальну висоту баскетбольного кільця, щоб бути _________ футів; це означає, що обруч не може бути _____________ ніж ця висота.

Напишіть дві нерівності - одна, щоб показати вашу оцінку мінімальної висоти баскетбольного кільця, а інша - для максимальної висоти. Використовуйте символ нерівності та змінну для представлення невідомої висоти.
Побудуйте кожну оцінку для мінімального або максимального значення на числовому рядку.

Мінімум:

Максимум:

Припустимо, однокласник оцінив$h$ значення 19 футів. Чи згодна ця оцінка з вашою нерівністю для максимальної висоти? Чи згоден він з вашою нерівністю на мінімальну висоту? Поясніть або покажіть, як ви знаєте.
Попросіть у партнера оцінку$h$. Запишіть кошторис і перевірте, чи згодна вона з вашими нерівностями для максимальної та мінімальної висоти.

Ви готові до більшого?

Знайдіть 3 різних числа, які$a$ могли б бути, якщо$|a|<5$. Покладіть ці точки на числовій лінії. Потім сюжет як багато інших можливостей для$a$, як ви можете.

Знайдіть 3 різних числа, які$b$ могли б бути, якщо$|b|>3$. Покладіть ці точки на числовій лінії. Потім сюжет як багато інших можливостей для$b$, як ви можете.

Резюме

Нерівність говорить нам, що одне значення менше або більше іншого значення.

Припустимо, ми знали, що температура менше$3^{\circ}\text{F}$, але ми точно не знаємо, що це таке. Щоб уявити те, що ми знаємо про температуру$t$ в$^{\circ}\text{F}$ ми можемо написати нерівність:$t<3$

Температуру також можна позначити на цифровому рядку. Будь-яка точка зліва від 3 є можливим значенням для$t$. Відкрите коло при 3 означає, що$t$ не може бути рівним 3, тому що температура менше 3.

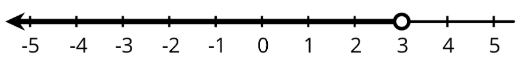
Ось ще один приклад. Припустимо, молодому мандрівникові має бути не менше 16 років, щоб літати на літаку без супроводжуючого дорослого.

Якщо$a$ позначає вік мандрівника, будь-яке число більше 16 є можливим значенням для$a$, а саме 16 також є можливим значенням$a$. Ми можемо показати це на числовій лінії, намалювавши замкнуте коло у 16 років, щоб показати, що воно відповідає вимогам (16-річна людина може подорожувати самостійно). Звідти проводимо лінію, яка вказує вправо.

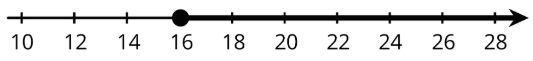
Ми також можемо написати нерівність і рівняння, щоб показати можливі значення для$a$:

$a>16$

$a=16$

Практика

Вправа$\PageIndex{4}$

На книжковому продажу всі книги коштують менше 5 доларів.

Якою може бути найдорожча книга?
Напишіть нерівність, щоб представляти витрати на книги при продажу.
Намалюйте числову лінію, щоб представити нерівність.

Вправа$\PageIndex{5}$

Кіран розпочав домашнє завдання до 19:00 і закінчив домашнє завдання після 20:00 Давайте$h$ представляємо кількість годин, які Кіран працював над домашнім завданням.

Вирішіть, якщо кожне твердження це, безумовно, вірно, безумовно, не вірно, або, можливо, вірно. Поясніть свої міркування.

$h>1$
$h>2$
$h<1$
$h<2$

Вправа$\PageIndex{6}$

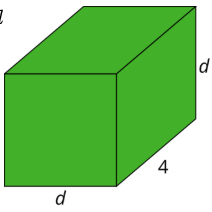
Розглянемо прямокутну призму довжиною 4 і шириною і висотою$d$.

Знайти вираз для обсягу призми в терміні$d$.
Обчислити обсяг призми коли$d=1$$d=2$, коли і коли$d=\frac{1}{2}$.

(З блоку 6.3.3)

Вправа$\PageIndex{7}$

Зіставте твердження, написані англійською мовою, з математичними твердженнями. Всі ці твердження відповідають дійсності.

Число -15 знаходиться далі від 0, ніж число -12 на числовому рядку.
Число -12 - це відстань 12 одиниць від 0 на числовому рядку.
Відстань між -12 і 0 на числовому рядку більше -15.
Числа 12 і -12 на однаковій відстані від 0 на числовому рядку.
Число -15 менше числа -12.
Число 12 більше числа -12.

$|-12|>-15$
$-15<-12$
$|-15|>|-12|$
$|-12|=12$
$12>-12$
$|12|=|-12|$

Вправа$\PageIndex{8}$

Ось п'ять сум. Використовуйте розподільну властивість, щоб записати кожну суму як добуток з двома факторами.

$2a+7a$
$5z-10$
$c-2cd$
$r+r+r+r$
$2x-\frac{1}{2}$

(З блоку 6.2.6)