37.3: Інтерпретація нерівностей

Last updated
Save as PDF

Page ID: 878

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Урок

Давайте розберемо, про що нам можуть розповісти нерівності.

Вправа\(\PageIndex{1}\): True or False: Fractions and Decimals

Кожне рівняння істинне чи хибне? Будьте готові пояснити свої міркування.

\(3(12+5)=(3\cdot 12)\cdot (3\cdot 5)\)
\(\frac{1}{3}\cdot\frac{3}{4}=\frac{3}{4}\cdot\frac{2}{6}\)
\(2\cdot (1.5)\cdot 12=4\cdot (0.75)\cdot 6\)

Вправа\(\PageIndex{2}\): Basketball Game

Ной набрав\(n\) очки в баскетбольному матчі.

Що\(15<n\) означає в контексті баскетбольної гри?
Що\(n<25\) означає в контексті баскетбольної гри?
Намалюйте дві числові лінії, щоб представити розв'язки двох нерівностей.
Назвіть можливе значення для\(n\) вирішення обох нерівностей.
Назвіть можливе значення для\(n\) цього рішення\(15<n\), але не рішення\(n<25\).
Чи може -8 бути рішенням\(n\) у цьому контексті? Поясніть свої міркування.

Вправа\(\PageIndex{3}\): Unbalanced Hangers

Ось схема незбалансованої вішалки.

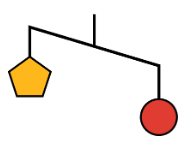
Джада каже, що вага одного кола більше ваги одного п'ятикутника. Напишіть нерівність, щоб представити її твердження. \(p\)Дозволяти бути вагою одного п'ятикутника і\(c\) бути вагою одного кола.
Коло важить 12 унцій. Використовуйте цю інформацію, щоб написати іншу нерівність для представлення співвідношення ваг. Потім опишіть, що означає ця нерівність у цьому контексті.

Ось ще одна схема незбалансованої вішалки.

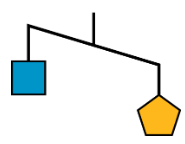
Напишіть нерівність, щоб представити співвідношення ваг. \(p\)Дозволяти бути вагою одного п'ятикутника і\(s\) бути вагою одного квадрата.
Один п'ятикутник важить 8 унцій. Використовуйте цю інформацію, щоб написати іншу нерівність для представлення співвідношення ваг. Потім опишіть, що означає ця нерівність у цьому контексті.
Графік розв'язків цієї нерівності на числовій лінії.

Виходячи з вашої роботи до цих пір, чи можете ви сказати взаємозв'язок між вагою квадрата та вагою кола? Якщо так, напишіть нерівність, щоб представити ці відносини. Якщо ні, поясніть свої міркування.
Це ще одна схема незбалансованої вішалки.

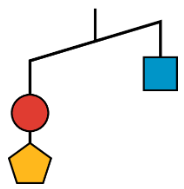
Андре пише наступне нерівність:\(c+p<s\). Чи згодні ви з його нерівністю? Поясніть свої міркування.

Джада дивиться на іншу діаграму незбалансованого ангара і пише:\(s+c>2t\), де\(t\) представляє вагу одного трикутника. Намалюйте ескіз схеми.

Ви готові до більшого?

Ось картина збалансованої вішалки. Він показує, що загальна вага трьох трикутників така ж, як загальна вага чотирьох квадратів.

Що це говорить вам про вагу одного квадрата в порівнянні з одним трикутником? Поясніть, як ви знаєте.
Напишіть рівняння або нерівність, щоб описати зв'язок між вагою квадрата та вагою трикутника. \(s\)Дозволяти бути вага квадрата і\(t\) бути вагою трикутника.

Резюме

Коли ми знаходимо рішення нерівності, ми повинні ретельно продумати її контекст. Число може бути рішенням нерівності поза контекстом, але може не мати сенсу, якщо розглядати його в контексті.

Припустимо, баскетболіст набрав більше 11 очок у грі, і ми представляємо кількість очок, які вона набрала\(s\), з нерівністю\(s>11\). Дивлячись лише на\(s>11\), ми можемо сказати, що такі числа, як\(12, 14\frac{1}{2},\) і\(130.25\) всі рішення нерівності, тому що кожен з них робить нерівність істинною.

\(12>11\qquad 14\frac{1}{2}>11\qquad 130.25>11\)

Однак у баскетбольній грі можна набрати лише цілу кількість очок, тому дробові та десяткові бали неможливі. Також вкрай малоймовірно, що одна людина набере більше 130 очок за одну гру.

Іншими словами, контекст нерівності може обмежувати її рішення.

Ось ще один приклад:

Рішення\(r<30\) можуть включати такі числа, як\(27\frac{3}{4}, 18.5, 0,\) і\(-7\). Але якщо\(r\) представляє кількість хвилин дощу вчора (а це зробив дощ), то наші рішення обмежені позитивними числами. Нульова або негативна кількість хвилин не мала б сенсу в цьому контексті.

Щоб показати верхню і нижню межі, ми можемо написати дві нерівності:

\(0<r\qquad r<30\)

Нерівності також можуть представляти порівняння двох невідомих чисел.

Припустимо, ми знали, що щеня важить більше, ніж кошеня, але ми не знали ваги жодної тварини. Ми можемо уявити вагу цуценя, в фунтах, з\(p\) і вага кошеня, в фунтах, с\(k\), і написати цю нерівність:\(p>k\)

Записи глосарію

Визначення: Розв'язок нерівності

Рішення нерівності - це число, яке може бути використано замість змінної, щоб зробити нерівність істинною.

Наприклад, 5 - це рішення нерівності\(c<10\), тому що це правда\(5<10\). Деякі інші рішення цієї нерівності - 9,9, 0 та -4.

Практика

Вправа\(\PageIndex{4}\)

У холодильнику Mai є закрита коробка яєць. Картонна коробка містить\(e\) яйце і вміщує 12 яєць.

Що\(e<12\) означає нерівність в цьому контексті?
Що\(e>0\) означає нерівність в цьому контексті?
Які можливі значення\(e\), які зроблять обидва\(e<12\) і\(e>0\) правдиві?

Вправа\(\PageIndex{5}\)

Ось схема незбалансованої вішалки.

Напишіть нерівність, щоб представити співвідношення ваг. Використовуйте\(s\) для представлення ваги квадрата в грамах і\(c\) для представлення ваги кола в грамах.
Один червоний коло важить 12 грам. Напишіть нерівність, щоб представляти вагу одного синього квадрата.
Чи може 0 бути значенням\(s\)? Поясніть свої міркування.

Вправа\(\PageIndex{6}\)

Джада вище Дієго. Дієго 54 дюйми заввишки (4 фути, 6 дюймів). Напишіть нерівність, яка порівнює висоту Джади в дюймах\(j\), з ростом Дієго.
Джада коротше Олени. Олена - 5 футів у висоту. Напишіть нерівність, яка порівнює зріст Джади в дюймах\(j\), з ростом Олени.

(З блоку 7.2.1)

Вправа\(\PageIndex{7}\)

Тайлер має більше 10 доларів. У Олени більше грошей, ніж у Тайлера. У Маї більше грошей, ніж у Олени. Нехай\(t\) буде сума грошей, яку має Тайлер, нехай\(e\) буде сума грошей, яку має Олена, і нехай\(m\) буде сума грошей, яку має Май. Виберіть усі твердження, які відповідають дійсності:

\(t<j\)
\(m>10\)
\(e>10\)
\(t>10\)
\(e>m\)
\(t<e\)

Вправа\(\PageIndex{8}\)

Що більше,\(\frac{-9}{20}\) або\(-0.5\)? Поясніть, як ви знаєте. Якщо ви застрягли, розглянути можливість побудови чисел на числовому рядку.

(З блоку 7.1.3)

Вправа\(\PageIndex{9}\)

Виділіть усі вирази, еквівалентні\(\left(\frac{1}{2}\right)^{3}\).

\(\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}\)
\(\frac{1}{2^{3}}\)
\(\left(\frac{1}{3}\right)^{2}\)
\(\frac{1}{6}\)
\(\frac{1}{8}\)

(З блоку 6.3.2)