Skip to main content
LibreTexts - Ukrayinska

28.4: Обчислення добутків десяткових знаків

  1. Last updated
  2. Save as PDF
  • Page ID
    826

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте множимо десяткові числа.

    Вправа\(\PageIndex{1}\): Number Talk: Twenty Times a Number

    Оцініть подумки.

    \(20\cdot 5\)

    \(20\cdot (0.8)\)

    \(20\cdot (0.04)\)

    \(20\cdot (5.84)\)

    Вправа\(\PageIndex{2}\): Calculating Products of Decimals

    1. Поширеним способом знайти добуток десяткових знаків є обчислення добутку цілих чисел, після чого розставити десяткову крапку в добутку.
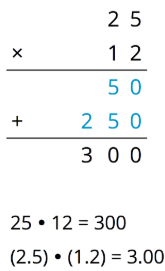
    clipboard_eaf43890faa64b730883ed40a894286a7.png
    Малюнок\(\PageIndex{1}\): Вертикальний розрахунок 25 разів 12, 5 рядів. Перший ряд: 25. Другий ряд: символ множення, 12. Горизонтальна лінія. Третій ряд: 50. Четвертий ряд: плюс 250. Горизонтальна лінія. П'ятий ряд: 300. Горизонтальний розрахунок, 25 разів 12 дорівнює 300. Горизонтальний розрахунок, 2 точка 5 разів 1 точка 2 дорівнює 3 точці 0 0.

    Ось приклад для\((2.5)\cdot (1.2)\).

    Використовуйте те, що ви знаєте про десяткові знаки та місце значення, щоб пояснити, чому десяткова крапка продукту розміщується там, де він знаходиться.

    1. Скористайтеся методом, показаним у першому рівнянні, для розрахунку кожного виробу.
      1. \((4.6)\cdot (0.9)\)
      2. \((16.5)\cdot (0.7)\)
    2. Використовуйте діаграми площ, щоб перевірити попередні розрахунки. Для кожної проблеми:
      • Розкладіть кожне число на його основу-десять одиниць і запишіть їх у квадрати з кожного боку прямокутника.
      • Запишіть область кожної літерної області на діаграмі. Потім знайдіть площу всього прямокутника. Покажіть свої міркування.
        1. \((4.6)\cdot (0.9)\)
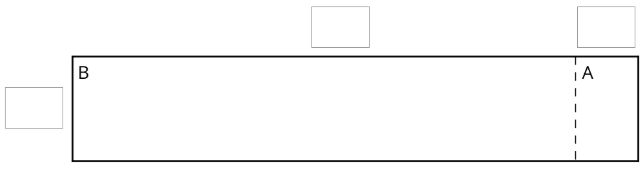
    clipboard_e9f1951403bb37be8b140d9e4cb07f6ae.png
    Малюнок\(\PageIndex{2}\)
    1. \((16.5)\cdot (0.7)\)
    clipboard_ed7d0b9a2eb210e7f38a72fb24f4cbf2a.png
    Малюнок\(\PageIndex{3}\)
    1. Про те, скільки сантиметрів в 6,25 дюймів, якщо 1 дюйм - це приблизно 2,5 сантиметра? Покажіть свої міркування.

    Вправа\(\PageIndex{3}\): Practicing Multiplication of Decimals

    1. Розрахуйте кожен товар. Покажіть свої міркування. Якщо ви застрягли, подумайте про те, щоб намалювати діаграму області, щоб допомогти.
      1. \((5.6)\cdot (1.8)\)
      2. \((0.008)\cdot (7.2)\)
    2. Прямокутна майданчик становить 18,2 метра на 12,75 метра.
      1. Знайти його площу в квадратних метрах. Покажіть свої міркування.
      2. Якщо 1 метр приблизно 3.28 футів, які приблизні довжини сторін дитячого майданчика в футах? Покажіть свої міркування.

    Ви готові до більшого?

    1. Запишіть наступні вирази у вигляді десяткових знаків.
      1. \(1-0.1\)
      2. \(1-0.1+10-0.01\)
      3. \(1-0.1+10-0.01+100-0.001\)
    2. Опишіть десяткове число, яке призводить до того, як цей процес триває.
    3. Що станеться з десятковим числом, якби всі символи додавання і віднімання стали символами множення? Поясніть свої міркування.

    Резюме

    Ми можемо використовувати\(84\cdot 43\) і те, що ми знаємо про значення місця, щоб знайти\((8.4)\cdot (4.3)\).

    Оскільки 8.4 становить 84 десятих і 4.3 - 43 десятих, то:

    \((8.4)\cdot (4.3)=\frac{84}{10}\cdot\frac{43}{10}=\frac{84\cdot 43}{100}\)

    Це означає, що ми можемо обчислити,\(84\cdot 43\) а потім розділити на 100, щоб знайти\((8.4)\cdot (4.3)\).

    \(84\cdot 43=3612\)

    \((8.4)\cdot (4.3)=36.12\)

    Використання дробів\(\frac{1}{10}\), таких як\(\frac{1}{100}\), і\(\frac{1}{1,000}\) дозволяє знайти добуток двох десяткових знаків за допомогою наступних кроків:

    • Запишіть кожен десятковий множник як добуток цілого числа і дробу.
    • Помножте цілі числа.
    • Множимо дроби.
    • Помножте добуток цілих чисел і дробів.

    Ми знаємо множення на дроби\(\frac{1}{10}\), такі як\(\frac{1}{100}\), і\(\frac{1}{1,000}\) це те саме, що ділення на 10, 100 і 1000 відповідно. Це означає, що ми можемо перемістити десяткову крапку у добутку цілого числа вліво відповідну кількість пробілів, щоб правильно розмістити десяткову крапку.

    Практика

    Вправа\(\PageIndex{4}\)

    Ось незакінчений розрахунок\((0.54)\cdot (3.8)\) і прямокутник 0,54 на 3,8.

    clipboard_ebcebf01a9d1c60c35b5e4c8c8a3f548c.png
    Малюнок\(\PageIndex{4}\)
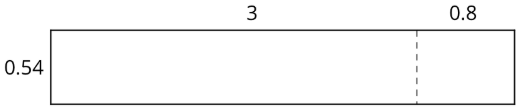
    clipboard_e2b05ad5f80afd20e2c44524053d3f565.png
    Малюнок\(\PageIndex{5}\)
    1. Яка частина прямокутника має площу 0,432? Яка частина прямокутника має площу 1,62? Покажіть свої міркування.
    2. Що таке\((0.54)\cdot (3.8)\)?

    Вправа\(\PageIndex{5}\)

    Поясніть, як продукт 3 і 65 може бути використаний для пошуку\((0.03)\cdot (0.65)\).

    Вправа\(\PageIndex{6}\)

    Використовуйте вертикальний розрахунок, щоб знайти кожен товар.

    1. \((5.4)\cdot (2.4)\)
    2. \((1.67)\cdot (3.5)\)

    Вправа\(\PageIndex{7}\)

    Фунт чорниці коштує 3,98 долара, а фунт клементинів коштує 2,49 долара. Яка сукупна вартість 0,6 фунта чорниці та 1,8 фунта клементинів? Округлите відповідь до найближчого цента.

    Вправа\(\PageIndex{8}\)

    Завершіть розрахунки так, щоб кожен показував правильну суму або різницю.

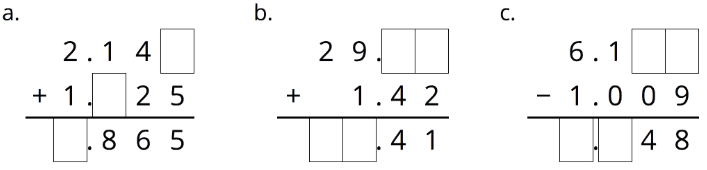
    clipboard_e4ac9b7e5859e52ebaa79d9d507245e0f.png
    Малюнок\(\PageIndex{6}\): 2 задачі десяткового додавання та 1 задача десяткового віднімання. Задача а. 2 пункт 1, 4, порожній + 1 і порожній, 2, 5 = порожній і 865 тисячних. Задача б. 29 точка порожня, порожня + 1 і 42 сотих = порожня точка 4, 1. Задача c. 6 пункт 1, порожній, порожній - 1 і 9 тисячних = порожній пункт, 4, 8.

    (З блоку 5.2.2)

    Вправа\(\PageIndex{9}\)

    Що має більшу цінність:\(7.4-0.0022\) або\(7.39-0.0012\)? Покажіть свої міркування.

    (Від блоку 5.2.3)

    Вправа\(\PageIndex{10}\)

    Андре висаджують саджанці (дитячі дерева). Йому потрібно 30 хвилин, щоб посадити 3 саджанця. Якщо на посадку кожного саджанця потрібно однакову кількість часу, скільки часу знадобиться Андре, щоб посадити 14 саджанців? Якщо ви застрягли, подумайте про використання таблиці.

    кількість саджанців час в хвилинах
    \(3\) \(30\)
    \(1\)
    \(14\)
    Таблиця\(\PageIndex{1}\)

    (Від блоку 2.4.2)