Skip to main content
LibreTexts - Ukrayinska

23.2: Використання алгоритму для поділу дробів

  1. Last updated
  2. Save as PDF
  • Page ID
    895

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте розділимо дроби за допомогою вивченого нами правила.

    Вправа\(\PageIndex{1}\): Multiplying Fractions

    Оцінити кожен вираз.

    1. \(\frac{2}{3}\cdot 27\)
    2. \(\frac{1}{2}\cdot\frac{2}{3}\)
    3. \(\frac{2}{9}\cdot\frac{3}{5}\)
    4. \(\frac{27}{100}\cdot\frac{200}{9}\)
    5. \(\left(1\frac{3}{4}\right)\cdot\frac{5}{7}\)

    Вправа\(\PageIndex{2}\): Dividing a Fraction by a Fraction

    Робота з партнером. Одна людина працює над питаннями з міткою «Партнер А», а інша людина працює над тими, які позначені «Партнер Б.»

    1. Партнер А:

    Знайдіть значення кожного виразу, заповнивши діаграму.

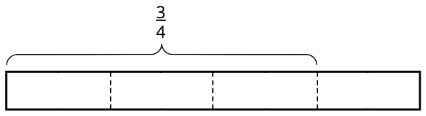
    1. \(\frac{3}{4}\div\frac{1}{8}\)

    Скільки\(\frac{1}{8}\) s в\(\frac{3}{4}\)?

    clipboard_e71833e4816a06ca2954cfd558426e68e.png
    Малюнок\(\PageIndex{1}\)
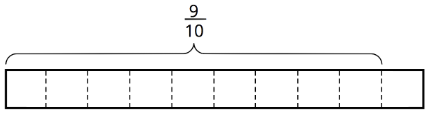
    1. \(\frac{9}{10}\div\frac{3}{5}\)

    Скільки\(\frac{3}{5}\) s в\(\frac{9}{10}\)?

    clipboard_ec0e9b4b0dfedb6ac9b6de403a61d415c.png
    Малюнок\(\PageIndex{2}\)

    Використовуйте аплет, щоб підтвердити свої відповіді та вивчити власні приклади.

    Партнер B:

    Олена сказала: «Якщо я хочу розділити 4 на\(\frac{2}{5}\), я можу помножити 4 на 5, а потім розділити на 2 або помножити на»\(\frac{1}{2}\).

    Знайдіть значення кожного виразу, використовуючи описану Оленою стратегію.

    1. \(\frac{3}{4}\div\frac{1}{8}\)
    2. \(\frac{9}{10}\div\frac{3}{5}\)
    1. Що ви помічаєте щодо діаграм і виразів? Обговоріть зі своїм партнером.
    2. Доповніть це речення, виходячи з того, що ви помітили:
      Щоб розділити число\(n\) на дріб\(\frac{a}{b}\), ми можемо\(n\) помножити на ________, а потім розділити твір на ________.
    3. Виберіть усі рівняння, які представляють завершену операцію.
      • \(n\div\frac{a}{b}=n\cdot b\div a\)
      • \(n\div\frac{a}{b}=n\cdot a\div b\)
      • \(n\div\frac{a}{b}=n\cdot\frac{a}{b}\)
      • \(n\div\frac{a}{b}=n\cdot\frac{b}{a}\)

    Вправа\(\PageIndex{3}\): Using an Algorithm to Divide Fractions

    Розрахуйте кожен коефіцієнт. Покажіть своє мислення і будьте готові пояснити свої міркування.

    1. \(\frac{8}{9}\div 4\)
    2. \(\frac{3}{4}\div\frac{1}{2}\)
    3. \(3\frac{1}{3}\div\frac{2}{9}\)
    4. \(\frac{9}{2}\div\frac{3}{8}\)
    5. \(6\frac{2}{5}\div 3\)
    6. \(5\frac{1}{2}\)Пройшовши велосипедні миль,\(\frac{2}{3}\) Джада подорожувала довжину своєї подорожі. Скільки часу (в милі) становить весь її відрізок? Напишіть рівняння, щоб представити ситуацію, а потім знайдіть відповідь.

    Ви готові до більшого?

    Припустимо, у вас є пінта виноградного соку і пінта молока. Вливаєте в молоко 1 столову ложку виноградного соку і перемішуєте. Потім виливаєте 1 столову ложку цієї суміші назад у виноградний сік. Яка рідина більш забруднена?

    Резюме

    Поділ\(a\div\frac{3}{4}=?\) еквівалентний\(\frac{3}{4}\cdot ?=a\), тому ми можемо думати про це як\(\frac{3}{4}\) значення «якого числа\(a\)?» і представляємо його діаграмою, як показано на малюнку. Довжина всієї діаграми являє собою невідоме число.

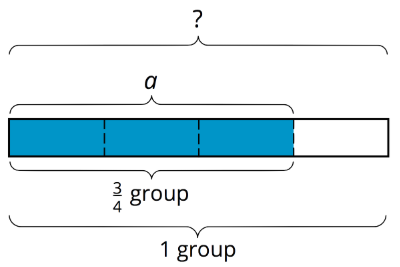
    clipboard_e5b8fd8145a3c3ef7665e301421eb56ab.png
    Малюнок\(\PageIndex{3}\): Лінійна діаграма дробів. 4 рівні частини. 3 частини заштриховані. Перші 3 частини маркуються фракцією 3 над 4 і а. всього маркуються невідомою кількістю і 1 групою.

    Якщо\(\frac{3}{4}\) числа є\(a\), то, щоб знайти число, ми можемо спочатку розділити\(a\) на 3, щоб знайти\(\frac{1}{4}\) число. Потім множимо результат на 4, щоб знайти число.

    Наведені вище кроки можна записати як:\(a\div 3\cdot 4\). Ділення на 3 - це те саме, що і множення на\(\frac{1}{3}\), тому ми також можемо записати кроки як:\(a\cdot\frac{1}{3}\cdot 4\).

    Іншими словами:\(a\div 3\cdot 4=a\cdot\frac{1}{3}\cdot 4\). І\(a\cdot\frac{1}{3}\cdot 4=a\cdot\frac{4}{3}\), таким чином, ми можемо сказати, що:

    \(a\div\frac{3}{4}=a\cdot\frac{4}{3}\)

    Взагалі, ділення числа на дріб\(\frac{c}{d}\) - це те ж саме, що і множення числа на\(\frac{d}{c}\), яке є зворотним дробу.

    Записи глосарію

    Визначення: Взаємний

    Ділення 1 на число дає зворотне це число. Наприклад,\(12\) взаємне є\(\frac{1}{12}\), а\(\frac{2}{5}\) взаємне є\(\frac{5}{2}\).

    Практика

    Вправа\(\PageIndex{4}\)

    Виділіть всі твердження, які показують правильні міркування для пошуку\(\frac{14}{15}\div\frac{7}{5}\).

    1. Множення\(\frac{14}{15}\) на,\(5\) а потім на\(\frac{1}{7}\).
    2. \(\frac{14}{15}\)Діливши на\(5\), а потім множимо на\(\frac{1}{7}\).
    3. Множення\(\frac{14}{15}\) на\(7\), а потім множення на\(\frac{1}{5}\).
    4. Множення\(\frac{14}{15}\) на,\(5\) а потім ділення на\(7\).
    5. Множення\(\frac{15}{14}\) на,\(7\) а потім ділення на\(5\).

    Вправа\(\PageIndex{5}\)

    Клер сказала, що\(\frac{4}{3}\div\frac{5}{2}\) так\(\frac{10}{3}\). Вона міркувала:\(\frac{4}{3}\cdot 5=\frac{20}{3}\) і\(\frac{20}{3}\div 2=\frac{10}{3}\).

    Поясніть, чому відповідь Клер і міркування невірні. Знайдіть правильний коефіцієнт.

    Вправа\(\PageIndex{6}\)

    Знайдіть значення\(\frac{15}{4}\div\frac{5}{8}\). Покажіть свої міркування.

    Вправа\(\PageIndex{7}\)

    Розглянемо проблему: Кіран має\(2\frac{3}{4}\) кілограми борошна. Коли він ділить борошно на однакові за розміром мішки, він заповнює\(4\frac{1}{8}\) мішки. Скільки фунтів вміщається в кожну сумку?

    Напишіть рівняння множення та рівняння ділення, щоб представити питання. Потім знайдіть відповідь і покажіть свої міркування.

    Вправа\(\PageIndex{8}\)

    Розділіть\(4\frac{1}{2}\) на кожну з цих одиниць дробу.

    1. \(\frac{1}{8}\)
    2. \(\frac{1}{4}\)
    3. \(\frac{1}{6}\)

    (Від блоку 4.3.1)

    Вправа\(\PageIndex{9}\)

    Розглянемо проблему: Після зарядки протягом\(\frac{1}{3}\) години телефон знаходиться на\(\frac{2}{5}\) повній потужності. Скільки часу знадобиться телефону, щоб повністю зарядитися?

    Вирішіть, чи може кожне рівняння представляти ситуацію.

    1. \(\frac{1}{3}\cdot ?=\frac{2}{5}\)
    2. \(\frac{1}{3}\div\frac{2}{5}=?\)
    3. \(\frac{2}{5}\div\frac{1}{3}=?\)
    4. \(\frac{2}{5}\cdot ?=\frac{1}{3}\)

    (Від блоку 4.2.6)

    Вправа\(\PageIndex{10}\)

    Олена і Ной кожен наповнюють відро водою. Відро Ноя\(\frac{2}{5}\) заповнене, а вода важить\(2\frac{1}{2}\) кілограми. Скільки важить вода Олени, якщо її відро заповнене, а відро ідентичне Ною?

    1. Напишіть рівняння множення та ділення, щоб представити питання.
    2. Намалюйте діаграму, щоб показати взаємозв'язок між величинами і знайти відповідь.

    (Від блоку 4.2.5)