4.8: Графічні системи лінійних нерівностей

Цілі навчання

До кінця цього розділу ви зможете:

• Визначити, чи є впорядкована пара розв'язком системи лінійних нерівностей
• Розв'яжіть систему лінійних нерівностей шляхом побудови графіків
• Розв'язуйте програми систем нерівностей

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Вирішити нерівність\(2a<5a+12\).
   Якщо ви пропустили цю проблему, перегляньте [посилання].
2. Визначте, чи\((3,12)\) є впорядкована пара рішенням системи\(y>2x+3\).
   Якщо ви пропустили цю проблему, перегляньте [посилання].

Визначити, чи є впорядкована пара розв'язком системи лінійних нерівностей

Визначення системи лінійних нерівностей дуже схоже на визначення системи лінійних рівнянь.

Визначення: Система лінійних нерівностей

Дві або більше лінійних нерівностей, згрупованих разом, утворюють систему лінійних нерівностей.

Система лінійних нерівностей виглядає як система лінійних рівнянь, але вона має нерівності замість рівнянь. Тут показано систему двох лінійних нерівностей.

\[\left\{\begin{array} {l} x+4y\geq 10\\3x−2y<12\end{array}\right.\nonumber\]

Для розв'язання системи лінійних нерівностей знайдемо значення змінних, які є розв'язками обох нерівностей. Розв'язуємо систему за допомогою графіків кожної нерівності і показуємо рішення у вигляді графа. Ми знайдемо область на площині, яка містить усі впорядковані пари\((x,y)\), які роблять обидві нерівності істинними.

Розв'язки системи лінійних нерівностей

Розв'язки системи лінійних нерівностей - це значення змінних, які роблять всі нерівності істинними.

Розв'язок системи лінійних нерівностей показано у вигляді затіненої області в системі\(xy\) -координат, яка включає всі точки, впорядковані пари яких роблять нерівності істинними.

Щоб визначити, чи є впорядкована пара розв'язком системи двох нерівностей, підставляємо значення змінних в кожну нерівність. Якщо впорядкована пара робить обидві нерівності істинними, це рішення для системи.

Приклад\(\PageIndex{1}\)

Визначте, чи є впорядкована пара рішенням системи\(\left\{\begin{array} {l} x+4y\geq 10\\3x−2y<12\end{array}\right.\)

а.\((−2,4)\) б.\((3,1)\)

Рішення:

а Чи є впорядкована\((−2,4)\) пара рішенням?

Впорядкована пара\((−2,4)\) зробила обидві нерівності вірними. Тому\((−2,4)\) є рішенням цієї системи.

b Чи є впорядкована\((3,1)\) пара рішенням?

Впорядкована пара\((3,1)\) зробила одну нерівність істинною, а іншу помилковою. Тому не\((3,1)\) є рішенням цієї системи.

Спробуйте! \(\PageIndex{1}\)

Визначте, чи є впорядкована пара рішенням системи:\(\left\{ \begin{array} {l} x−5y>10\\2x+3y>−2 \end{array} \right.\)

а.\((3,−1)\) б.\((6,−3)\)

Відповідь

а. ні
б. так

Спробуйте! \(\PageIndex{2}\)

Визначте, чи є впорядкована пара рішенням системи:\(\left\{ \begin{array} {l} y>4x−2\\4x−y<20 \end{array} \right.\)

а.\((−2,1)\) б.\((4,−1)\)

Відповідь

а. так
б. ні

Розв'язувати систему лінійних нерівностей за допомогою графіків

Розв'язком єдиної лінійної нерівності є область з одного боку граничної лінії, яка містить всі точки, які роблять нерівність істинною. Розв'язок системи двох лінійних нерівностей - це область, яка містить розв'язки обох нерівностей. Щоб знайти цей регіон, ми проведемо графік кожної нерівності окремо, а потім знайдемо регіон, де вони обидва є істинними. Рішення завжди відображається у вигляді графіка.

Приклад\(\PageIndex{2}\): How to Solve a System of Linear Inequalities by Graphing

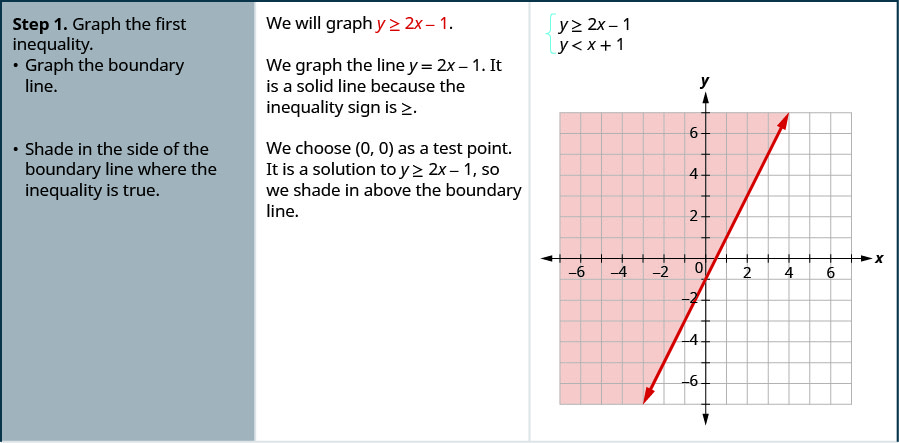
Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} y\geq 2x−1 \\ y<x+1\end{array}\right.\)

Рішення:

Спробуйте! \(\PageIndex{3}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} y<3x+2\\y>−x−1\end{array}\right.\)

Відповідь

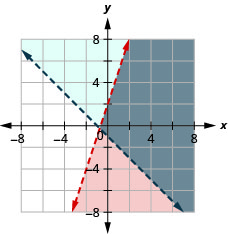
Рішення - сіра область.

Спробуйте! \(\PageIndex{4}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} y<−12x+3 \\ y<3x−4\end{array}\right.\)

Відповідь

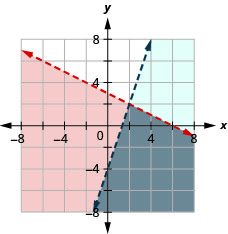
Рішення - сіра область.

Розв'язувати систему лінійних нерівностей за допомогою графіків

1. Графік першої нерівності.
   • Графік лінії кордону.
   • Затінення в стороні лінії кордону, де нерівність є істинною.
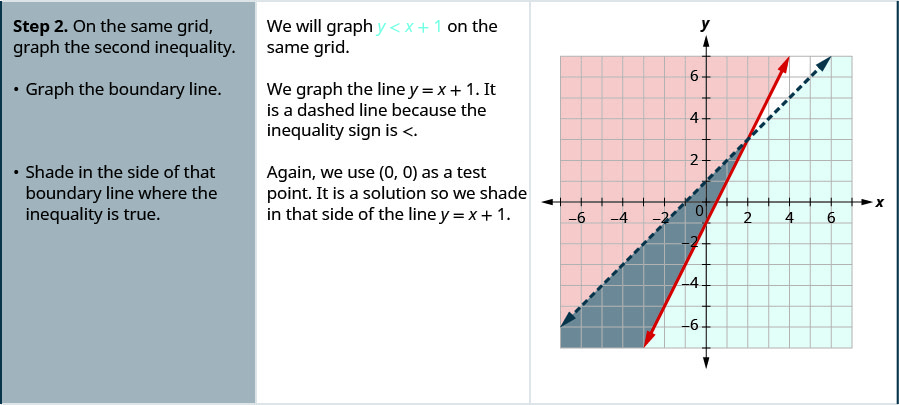
2. На тій же сітці намалюйте другу нерівність.
   • Графік лінії кордону.
   • Затінення в стороні тієї граничної лінії, де нерівність є істинною.
3. Рішення - область, де затінення перекривається.
4. Перевірте, вибравши контрольний пункт.

Приклад\(\PageIndex{3}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} x−y>3\\y<−15x+4\end{array}\right.\)

Рішення:

	\(\left\{\begin{array} {l} x−y>3\\y<−15x+4\end{array}\right.\)
Графік\(x - y > 3,\) шляхом побудови графіків\(x - y = 3\) і тестування точки. Перехоплення є\(x = 3\)\(y = −3\) і лінія кордону буде пунктирною. Тест\((0, 0)\), який робить нерівність помилковою, так що затіньте (червоний) сторону, яка не містить\((0, 0).\)

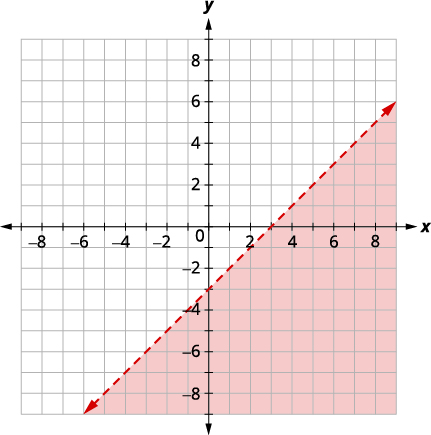Графік\(y<−15x+4\) за допомогою графіків з\(y=−15x+4\) використанням нахилу\(m=−15\) та\(y\) -перехоплення\(b = 4.\) межова лінія буде пунктирною Тест,\((0, 0)\) що робить нерівність істинною, тому тінь (синя) сторона, яка містить\((0, 0).\) Виберіть контрольну точку в розчині та переконайтеся, що це рішення обох нерівностей.

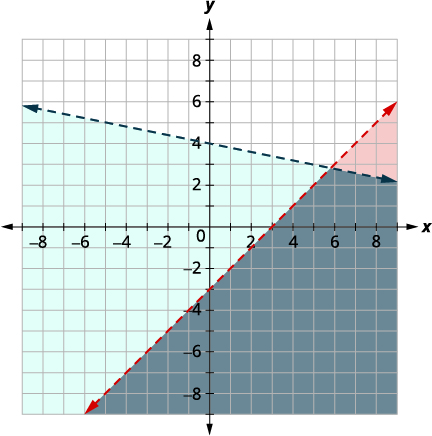Точка перетину двох ліній не включається, оскільки обидві лінії кордону були пунктирними. Рішенням є область, затінена двічі, яка виглядає як найтемніша затінена область.

Спробуйте! \(\PageIndex{5}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} x+y\leq 2 \\ y\geq \frac{2}{3}x−1\end{array}\right.\)

Відповідь

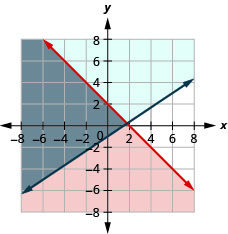
Рішення - сіра область.

Спробуйте! \(\PageIndex{6}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} 3x−2y\leq 6\\y>−\frac{1}{4}x+5\end{array} \right.\)

Відповідь

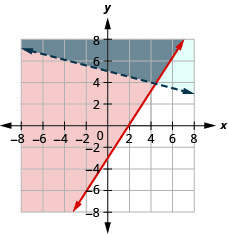
Рішення - сіра область.

Приклад\(\PageIndex{4}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} x−2y<5\\y>−4\end{array}\right.\)

Рішення:

	\(\left\{\begin{array} {l} x−2y<5\\y>−4\end{array}\right.\)
Графік\(x−2y<5\), шляхом побудови графіків\(x−2y=5\) і тестування точки. Перехоплення є\(x = 5\)\(y = −2.5\) і межа буде пунктирною. Тест\((0, 0)\), який робить нерівність істинною, тому затінюйте (червону) сторону, яка містить\((0, 0).\)

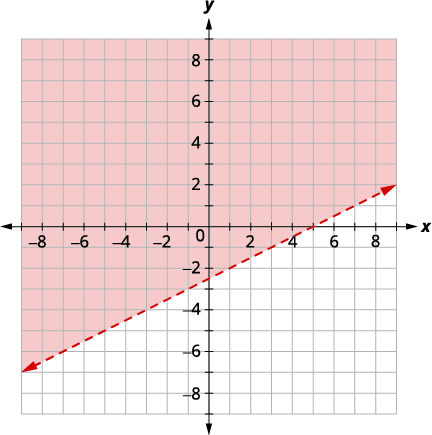Графік\(y>−4\), шляхом побудови\(y=−4\) графіків і визнання того, що це горизонтальна лінія через\(y=−4\). Лінія кордону буде пунктирною. Тест\((0, 0)\), який робить нерівність істинною, так що тінь (синій) сторона, яка містить\((0, 0).\)

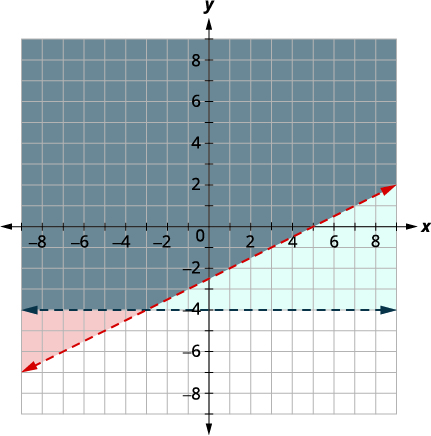\((0,0)\)Справа в розв'язанні, і ми вже знайшли, що це рішення кожної нерівності. Точка перетину двох ліній не включається, оскільки обидві лінії кордону були пунктирними.

Рішенням є область, затінена двічі, яка виглядає як найтемніша затінена область.

Спробуйте! \(\PageIndex{7}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} y\geq 3x−2 \\ y<−1\end{array}\right.\)

Відповідь

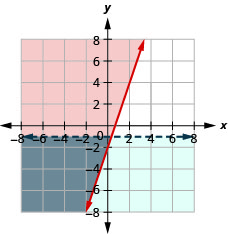
Рішення - сіра область.

Спробуйте! \(\PageIndex{8}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} x>−4x−2 \\ y\geq −4 \end{array}\right.\)

Відповідь

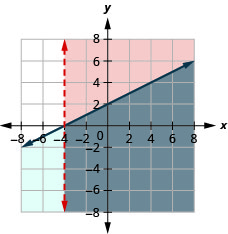
Рішення - сіра область.

Системи лінійних нерівностей, де граничні лінії паралельні, можуть не мати розв'язку. Ми побачимо це в наступному прикладі.

Приклад\(\PageIndex{5}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} 4x+3y\geq 12 \\ y<−\frac{4}{3}x+1\end{array}\right.\)

Рішення:

	\(\left\{\begin{array} {l} 4x+3y\geq 12 \\ y<−\frac{4}{3}x+1\end{array}\right.\)
Графік\(4x+3y\geq 12\), шляхом побудови графіків\(4x+3y=12\) і тестування точки. Перехоплення є\(x = 3\) \(y = 4\) і межа буде суцільною. Тест,\((0, 0)\) який робить нерівність помилковою, тому затінюйте (червону) сторону, яка не містить\((0, 0).\)
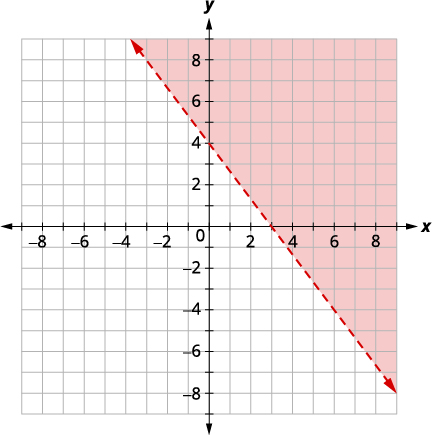Графік\(y<−\frac{4}{3}x+1\) за допомогою\(y=−\frac{4}{3}x+1\) графіків з використанням нахилу\(m=−\frac{4}{3}\) та\(y\) -перехоплення\(b = 1.\) межова лінія буде пунктирною. Тест\((0, 0)\), який робить нерівність істинною, тому затінюйте (синю) сторону, яка містить\((0, 0).\)

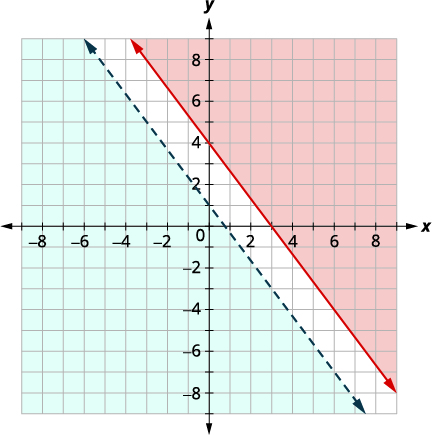Немає сенсу в обох затінених областях, тому система не має рішення.

Спробуйте! \(\PageIndex{9}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} 3x−2y\geq 12 \\ y\geq \frac{3}{2}x+1\end{array}\right.\)

Відповідь

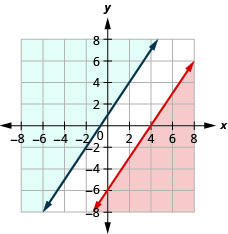
Немає рішення.

Спробуйте! \(\PageIndex{10}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} x+3y>8\\y<−\frac{1}{3}x−2\end{array}\right.\)

Відповідь

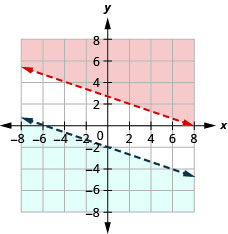
Немає рішення.

Деякі системи лінійних нерівностей, де граничні лінії паралельні, матимуть рішення. Ми побачимо це в наступному прикладі.

Приклад\(\PageIndex{6}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} y>\frac{1}{2}x−4\\x−2y<−4\end{array}\right.\)

Рішення:

	\(\left\{\begin{array} {l} y>\frac{1}{2}x−4\\x−2y<−4\end{array}\right.\)
Графік\(y>\frac{1}{2}x−4\) за допомогою\(y=\frac{1}{2}x−4\) графіків з використанням нахилу\(m=\frac{1}{2}\) та перехоплення\(b = −4.\) Лінія кордону буде пунктирною. Тест\((0, 0)\), який робить нерівність істинною, тому затінюйте (червону) сторону, яка містить\((0, 0).\)
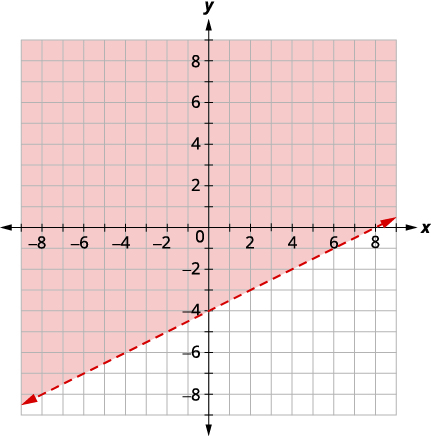Графік\(x−2y<−4\) шляхом побудови графіків\(x−2y=−4\) і тестування точки. Перехоплення є\(x = -4\) \(y=2\) і межа буде пунктирною. Виберіть контрольну точку в рішенні та переконайтеся , що це рішення обох нерівностей. Тест,\((0, 0)\) який робить нерівність помилковою, тому затінюйте (синю) сторону, яка не містить\((0, 0).\)

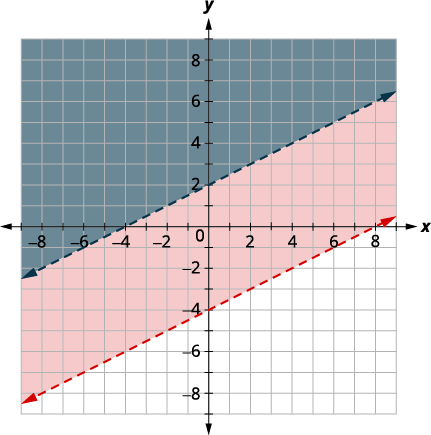Жодна точка на граничних лініях не включається до розв'язку, оскільки обидві лінії штрихові.

Рішення - це область, яка затінюється двічі, що також є рішенням\(x−2y<−4\).

Спробуйте! \(\PageIndex{11}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} y\geq 3x+1 \\ −3x+y\geq −4\end{array}\right.\)

Відповідь

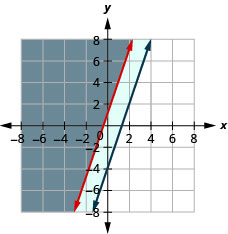
Рішення - сіра область.

Спробуйте! \(\PageIndex{12}\)

Вирішіть систему за допомогою графіків:\(\left\{\begin{array} {l} y\leq −\frac{1}{4}x+2\\x+4y\leq 4\end{array}\right.\)

Відповідь

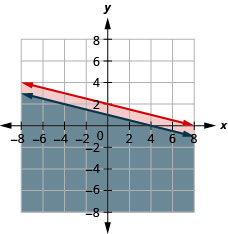
Рішення - сіра область.

Розв'язування застосувань систем нерівностей

Перше, що нам потрібно зробити для вирішення застосувань систем нерівностей, це перевести кожну умову в нерівність. Потім ми графуємо систему, як ми робили вище, щоб побачити регіон, який містить рішення. Багато ситуацій будуть реалістичними тільки в тому випадку, якщо обидві змінні будуть позитивними, тому ми додаємо нерівності в систему як додаткові вимоги.

Приклад\(\PageIndex{7}\)

Крісті продає свої фотографії на стенді на вуличному ярмарку. На початку дня вона хоче мати принаймні 25 фотографій для відображення на своєму стенді. Кожна маленька фотографія, яку вона відображає, коштує їй 4 долари, а кожна велика фотографія коштує її 10 доларів. Вона не хоче витрачати більше 200 доларів на фотографії для відображення.

а) Напишіть систему нерівностей для моделювання цієї ситуації.
б Графік системи.
c Чи може вона відображати 10 маленьких і 20 великих фотографій?
d Чи може вона відображати 20 великих і 10 маленьких фотографій?

Рішення:

а.
\(\begin{array} {ll} \text{Let} &{x=\text{the number of small photos.}} \\ {} &{y=\text{the number of large photos}}\end{array}\)

Щоб знайти систему рівнянь, переведіть інформацію.

\( \qquad \begin{array} {l} \\ \\ \text{She wants to have at least 25 photos.} \\ \text{The number of small plus the number of large should be at least }25. \\ \hspace{45mm} x+y\geq 25 \\ \\ \\ $4 \text{ for each small and }$10\text{ for each large must be no more than }$200 \\ \hspace{40mm} 4x+10y\leq 200 \\ \\ \\ \text{The number of small photos must be greater than or equal to }0. \\ \hspace{50mm} x\geq 0 \\ \\ \\ \text{The number of large photos must be greater than or equal to }0. \\ \hspace{50mm} y\geq 0 \end{array} \)

У нас є система рівнянь.

\(\hspace{65mm} \left\{\begin{array} {l} x+y\geq 25 \\4x+10y\leq 200\\x\geq 0\\y\geq 0\end{array}\right.\)

b
Оскільки\(x\geq 0\) і\(y\geq 0\) (обидва більше або рівні) всі рішення будуть знаходитися в першому квадранті. В результаті наш графік показує тільки один квадрант.

Для\(x+y\geq 25\) графіка графуйте\(x+y=25\) як суцільну лінію. Виберіть\((0, 0)\) в якості тестової точки. Оскільки це не робить нерівність істинною, затіньте (червоний) сторону, яка не включає точку\((0, 0).\) До графіка\(4x+10y\leq 200\), граф\(4x+10y=200\) як суцільна лінія. Виберіть\((0, 0)\) в якості тестової точки. Оскільки це робить нерівність істинною, затіньте (синій) сторону, яка включає точку\((0, 0).\)

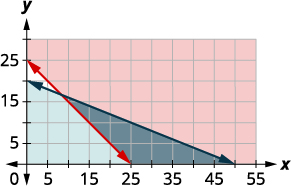Рішенням системи є область графіка, яка затінена найтемнішою. Розрізи лінії кордону, що межують темно затінену ділянку, включаються до розв'язку, як і точки на\(x\) осі -від\((25, 0)\) до\((55, 0).\)

c Щоб визначити, чи працюватимуть 10 малих та 20 великих фотографій, ми дивимося на графік, щоб побачити, чи\((10, 20)\) знаходиться точка в області рішення. Ми також могли б перевірити точку, щоб побачити, чи це рішення обох рівнянь.

Це не так, Крісті не показувала б 10 маленьких і 20 великих фотографій.

d Щоб визначити, чи працюватимуть 20 малих та 10 великих фотографій, ми дивимося на графік, щоб побачити, чи\((20, 10)\) знаходиться точка в області рішення. Ми також могли б перевірити точку, щоб побачити, чи це рішення обох рівнянь.

Це так, щоб Крісті міг вибрати для відображення 20 маленьких і 10 великих фотографій.

Зверніть увагу, що ми також могли б перевірити можливі рішення, підставляючи значення в кожну нерівність.

Спробуйте! \(\PageIndex{13}\)

Причіп може перевозити максимальну вагу 160 фунтів і максимальний об'єм 15 кубічних футів. Мікрохвильова піч важить 30 фунтів і має 2 кубічних фути об'єму, тоді як принтер важить 20 фунтів і має 3 кубічні фути простору.

а) Напишіть систему нерівностей для моделювання цієї ситуації.
б Графік системи.
c Чи можна перевозити 4 мікрохвильові печі та 2 принтери на цьому причепі?
d Чи можна перевозити на цьому причепі 7 мікрохвильових печей та 3 принтерів?

Відповідь

а.\(\left\{\begin{array} {l} 30m+20p\leq 160\\2m+3p\leq 15\end{array}\right.\)
б.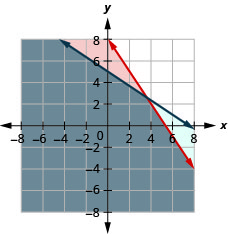

c. так
d. ні

Спробуйте! \(\PageIndex{14}\)

Мері потрібно придбати запаси листів відповідей та олівці для стандартизованого тесту, який буде надано молодшим у своїй середній школі. Кількість необхідних листів відповідей як мінімум на 5 більше, ніж кількість олівців. Олівці коштують 2 долари, а листи відповідей коштують $1. Бюджет Марії на ці поставки дозволяє отримати максимальну вартість 400 доларів.

а) Напишіть систему нерівностей для моделювання цієї ситуації.
б Графік системи.
c Чи могла Мері придбати 100 олівців і 100 аркушів відповідей?
d Чи могла Мері придбати 150 олівців і 150 аркушів відповідей?

Відповідь

а.\(\left\{\begin{array} {l} a\geq p+5 \\ a+2p\leq 400\end{array}\right.\)
б.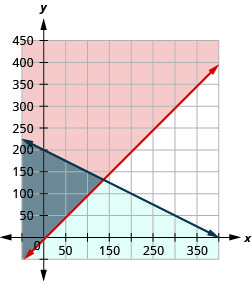

c. ні
d. ні

Коли ми використовуємо змінні, крім\(x\) і\(y\) для визначення невідомої величини, ми також повинні змінити імена осей графіка.

Приклад\(\PageIndex{8}\)

Омару потрібно з'їсти щонайменше 800 калорій, перш ніж йти на свою командну практику. Все, що він хоче, - це гамбургери та печиво, і він не хоче витрачати більше 5 доларів. У ресторані гамбургерів біля його коледжу кожен гамбургер має 240 калорій і коштує $1,40. Кожне печиво має 160 калорій і коштує 0,50 долара.

а) Напишіть систему нерівностей для моделювання цієї ситуації.
б Графік системи.
c Чи міг він з'їсти 3 гамбургери і 1 печиво?
d Чи міг він з'їсти 2 гамбургери і 4 печива?

Рішення:

а.
\(\begin{array} {ll} \text{Let} & h=\text{the number of hamburgers.} \\ & c=\text{the number of cookies}\end{array}\)

Щоб знайти систему рівнянь, переведіть інформацію.

Калорії гамбургерів по 240 калорій кожен, плюс калорії з печива на 160 калорій кожен повинен бути більше 800.

\(\qquad \begin{array} {l} \hspace{40mm} 240h+160c\geq 800 \\ \\ \\ \text{The amount spent on hamburgers at }$1.40\text{ each, plus the amount spent on cookies}\\\text{at }$0.50\text{ each must be no more than }$5.00.\\ \hspace{40mm} 1.40h+0.50c\leq 5 \\ \\ \\ \text{The number of hamburgers must be greater than or equal to 0.} \\ \hspace{50mm} h\geq 0 \\ \text{The number of cookies must be greater than or equal to 0.}\\ \hspace{50mm} c\geq 0 \end{array} \)

\(\text{We have our system of equations.} \qquad \left\{ \begin{array} {l} 240h+160c\geq 800 \\ 1.40h+0.50c\leq 5 \\ h\geq 0 \\ c\geq 0\end{array} \right.\)

b
Оскільки\(h\geq 0\) і\(c\geq 0\) (обидва більше або рівні) всі рішення будуть знаходитися в першому квадранті. В результаті наш графік показує тільки один квадрант.

Для\(240h+160c\geq 800\) графіка графуйте\(240h+160c=800\) як суцільну лінію. Виберіть\((0, 0)\) в якості тестової точки. Оскільки це не робить нерівність істинною, затінюйте (червоний) ту сторону, яка не включає точку\((0, 0).\)

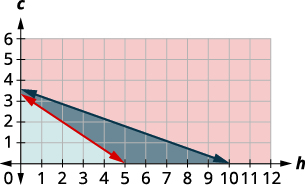Графік\(1.40h+0.50c\leq 5\). Лінія кордону - це\(1.40h+0.50c=5\). Ми тестуємо,\((0, 0)\) і це робить нерівність правдою. Розтушовуємо сторону лінії, яка включає\((0, 0).\)

Рішенням системи є область графіка, яка затінена найтемнішою. Розрізи лінії кордону, що межують темно затінену ділянку, включаються до розв'язку, як і точки на\(x\) осі -від\((5, 0)\) до\((10, 0).\)

c Щоб визначити, чи відповідають 3 гамбургери та 2 печива критеріям Омара, ми бачимо, чи\((3, 2)\) справа в регіоні рішення. Це так, тому Омар може вибрати, щоб з'їсти 3 гамбургери і 2 печива.

d Щоб визначити, чи відповідають 2 гамбургери та 4 печива критеріям Омара, ми бачимо, чи\((2, 4)\) справа в регіоні рішення. Це, Омар може вибрати, щоб з'їсти 2 гамбургери і 4 печива.

Ми також могли б перевірити можливі рішення, підставляючи значення в кожну нерівність.

Спробуйте! \(\PageIndex{15}\)

Напруженість повинна з'їдати принаймні зайву 1000 калорій на день, щоб підготуватися до бігу марафону. Він має тільки $25, щоб витратити на додаткову їжу, яку він потребує, і витратить його на $0.75 пончики, які мають 360 калорій кожен і $2 енергетичних напоїв, які мають 110 калорій.

а) Напишіть систему нерівностей, яка моделює цю ситуацію.
б Графік системи.
c Чи може він купити 8 пончиків і 4 енергетичних напою і задовольнити свої потреби в калоріях?
d Чи може він купити 1 пончик і 3 енергетичних напою і задовольнити свої потреби в калоріях?

Відповідь

а.\(\left\{\begin{array} {l} 0.75d+2e\leq 25\\360d+110e\geq 1000\end{array}\right.\)
б.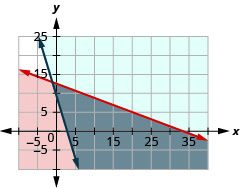

c. так
d. ні

Спробуйте! \(\PageIndex{16}\)

Лікар Філіпа каже йому, що він повинен додавати щонайменше 1000 калорій на день до звичного раціону. Філіп хоче придбати протеїнові батончики, які коштують 1,80 доларів кожен і мають 140 калорій та сік, який коштує 1,25 долара за пляшку та 125 калорій. Він не хоче витрачати більше 12 доларів.

а) Напишіть систему нерівностей, яка моделює цю ситуацію.
б Графік системи.
c. може він купити 3 протеїнові батончики і 5 пляшок соку?
d Чи може він купити 5 протеїнових батончиків і 3 пляшки соку?

Відповідь

а.\(\left\{\begin{array} {l} 140p+125j\geq 1000\\1.80p+1.25j\leq 12\end{array}\right.\)
б.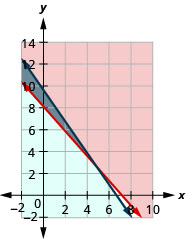

c. так
d. ні

Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з розв'язуванням систем лінійних нерівностей за допомогою графіків.

• Розв'язування систем лінійних нерівностей методом графування
• Системи лінійних нерівностей

Ключові концепції

• Розв'язки системи лінійних нерівностей: Розв'язки системи лінійних нерівностей - це значення змінних, які роблять усі нерівності істинними. Розв'язок системи лінійних нерівностей показано у вигляді затіненої області в системі\(xy\) -координат, яка включає всі точки, впорядковані пари яких роблять нерівності істинними.
• Як розв'язати систему лінійних нерівностей шляхом побудови графіків.
  1. Графік першої нерівності.
     Графік лінії кордону.
     Затінення в стороні лінії кордону, де нерівність є істинною.
  2. На тій же сітці намалюйте другу нерівність.
     Графік лінії кордону.
     Затінення в стороні тієї граничної лінії, де нерівність є істинною.
  3. Рішення - область, де затінення перекривається.
  4. Перевірте, вибравши контрольний пункт.

Глосарій

система лінійних нерівностей

Дві або більше лінійних нерівностей, згрупованих разом, утворюють систему лінійних нерівностей.