Глава 2 Огляд вправ

Last updated
Save as PDF

Page ID: 59779

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Розділ Огляд Вправи

Використання загальної стратегії для розв'язання лінійних рівнянь

Розв'язування рівнянь з використанням загальної стратегії розв'язання лінійних рівнянь

У наступних вправах визначте, чи є кожне число розв'язком рівняння.

1. $10x−1=5x,\quad x= \frac{1}{5}$

2. $−12n+5=8n,\quad n=−\frac{5}{4}$

Відповідь: ні

У наступних вправах розв'яжіть кожне лінійне рівняння.

3. $6(x+6)=24$

4. $−(s+4)=18$

Відповідь: $s=−22$Таким чином, набір рішень:$ \{-22\} $.

5. $23−3(y−7)=8$

6. $\frac{1}{3}(6m+21)=m−7$

Відповідь: $m=−14$

7. $4(3.5y+0.25)=365$

8. $0.25(q−8)=0.1(q+7)$

Відповідь: $q=18$

9. $8(r−2)=6(r+10)$

10. $5+7(2−5x)=2(9x+1)−(13x−57)$

Відповідь: $x=−1$

11. $(9n+5)−(3n−7)=20−(4n−2)$

12. $2[−16+5(8k−6)]=8(3−4k)−32$

Відповідь: $k=\frac{3}{4}$

Класифікувати рівняння

У наступних вправах класифікуйте кожне рівняння як умовне рівняння, ідентичність або протиріччя, а потім сформулюйте рішення.

13. $17y−3(4−2y)=11(y−1)+12y−1$

14. $9u+32=15(u−4)−3(2u+21)$

Відповідь: протиріччя; немає рішення

15. $−8(7m+4)=−6(8m+9)$

Вирішити рівняння з дробними або десятковими коефіцієнтами

У наступних вправах розв'яжіть кожне рівняння.

16. $\frac{2}{5}n−\frac{1}{10}=\frac{7}{10}$

Відповідь: $n=2$

17. $\frac{3}{4}a−\frac{1}{3}=\frac{1}{2}a+\frac{5}{6}$

18. $\frac{1}{2}(k+3)=\frac{1}{3}(k+16)$

Відповідь: $k=23$

19. $\frac{5y−1}{3}+4=\frac{-8y+4}{6}$

20. $0.8x−0.3=0.7x+0.2$

Відповідь: $x=5$

21. $0.10d+0.05(d−4)=2.05$

Використовуйте стратегію вирішення проблем

Використовуйте стратегію вирішення проблем для проблем Word

У наступних вправах вирішуйте, використовуючи стратегію вирішення проблем для слів.

22. Три чверті людей на концерті - діти. Якщо дітей 87, то яка загальна кількість людей на концерті?

Відповідь: Тут проживає 116 осіб.

23. У групі дев'ять саксофоністів. Кількість саксофоністів в один раз менше, ніж в два рази перевищує кількість гравців в тубу. Знайти кількість гравців в тубі.

Вирішити проблеми з числовим словом

У наступних вправах вирішуйте кожне число слово завдання.

24. Сума числа і трьох - сорок один. Знайдіть номер.

Відповідь: 38

25. Одне число на дев'ять менше іншого. Їх сума - від'ємна двадцять сім. Знайдіть цифри.

26. Одне число в два більше чотирьох разів інше. Їх сума - тринадцять негативних. Знайдіть цифри.

Відповідь: $−3,−10$

27. Сума двох послідовних цілих чисел дорівнює$−135$. Знайдіть цифри.

28. Знайдіть три послідовних парних цілих числа, сума яких дорівнює 234.

Відповідь: 76, 78, 80

29. Знайти три послідовних непарних цілих числа, сума яких дорівнює 51.

30. Коджі має $5,502 на своєму ощадному рахунку. Це на 30 доларів менше, ніж в шість разів перевищує суму на його розрахунковому рахунку. Скільки грошей у Коджі на своєму розрахунковому рахунку?

Відповідь: $922

Вирішити відсоток додатків

У наступних вправах перекладіть і вирішуйте.

31. Яке число 67% від 250?

32. 12,5% від якого числа 20?

Відповідь: $160$

33. Який відсоток 125 дорівнює 150?

У наступних вправах вирішуйте.

34. Рахунок за обід Діно становив $19,45. Він хотів залишити 20% від загальної суми рахунку в якості чайових. Скільки повинен бути чайовий?

Відповідь: $$3.89$

35. Долорес купила ліжечко на продаж за 350 доларів. Ціна продажу становила 40% від початкової ціни. Якою була початкова ціна ліжечка?

36. Джейден заробляє $2,680 на місяць. Він платить 938 доларів на місяць за оренду. Який відсоток його щомісячної зарплати йде на оренду?

Відповідь: $35%$

37. Ангел отримав підвищення своєї річної зарплати з $55,400 до $56 785. Знайдіть відсоток зміни.

38. Щомісячний рахунок за бензин Ровена знизився з $83,75 минулого місяця до $56.95 цього місяця. Знайдіть відсоток зміни.

Відповідь: $32%$

39. Emmett купив пару взуття на продаж зі знижкою 40% від початкової ціни 138 доларів. Знайти ⓐ суму знижки і ⓑ ціну продажу.

40. Лейсі купила пару чобіт у продажу за 95 доларів. Початкова ціна чобіт становила 200 доларів. Знайти ⓐ суму знижки і ⓑ ставку дисконту. (Округляйте до найближчої десятої частки відсотка, якщо потрібно.)

Відповідь: ⓐ$$105$ ⓑ$52.5%$

41. Нга і Лорен купили скриню на блошиному ринку за 50 доларів. Вони повторно закінчили його, а потім додали 350% націнки. Знайти ⓐ суму націнки і ⓑ прайс-лист.

Вирішіть прості програми для інтересів

У наступних вправах вирішуйте.

42. Вінстон внес $3,294 на банківський рахунок з процентною ставкою 2,6% Скільки відсотків було зароблено за п'ять років?

Відповідь: $$428.22$

43. Мойра позичила 4500 доларів у свого діда, щоб заплатити за перший рік коледжу. Через три роки вона погасила 4500 доларів плюс 243 відсотки. Якою була процентна ставка?

44. У заяві про кредит на рефрижератор Хайме говориться, що він заплатить 1,026 доларів у вигляді відсотків за чотирирічний кредит під 13,5%. Скільки позичив Хайме, щоб купити холодильник?

Відповідь: $$1,900$

Розв'яжіть формулу для конкретної змінної

Розв'яжіть формулу для певної змінної

У наступних вправах розв'яжіть формулу для зазначеної змінної.

45. Розв'яжіть формулу
$V=LWH$ для L.

46. Вирішити формулу
$A=\frac{1}{2}d_1d_2$ для$d_2$.

Відповідь: $d_2=\frac{2A}{d_1}$

47. Розв'яжіть формулу
$h=48t+\frac{1}{2}at^2$ для t.

48. Розв'яжіть формулу
4x−3y=12 для y.

Відповідь: $y=\frac{4x}{3}−4$

Використовуйте формули для вирішення геометрії додатків

У наступних вправах вирішуйте, використовуючи формулу геометрії.

49. Яка висота трикутника площею 67,567,5 квадратних метрів і підстави 9 метрів?

50. Міра найменшого кута в прямокутному трикутнику на 45° 45° менше, ніж міра наступного більшого кута. Знайдіть мірки всіх трьох кутів.

Відповідь: $22.5°,\; 67.5°,\; 90°$

51. Периметр трикутника становить 97 футів. Одна сторона трикутника на одинадцять футів більше найменшої сторони. Третя сторона - на шість футів більше, ніж в два рази найменша сторона. Знайдіть довжини всіх сторін.

52. Знайти довжину гіпотенузи.

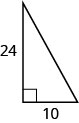
$Фігура являє собою прямокутний трикутник з основою в 10 одиниць і висотою 24 одиниці.$

Відповідь: $26$

53. Знайдіть довжину відсутньої сторони. Округлити до найближчої десятої, якщо це необхідно.

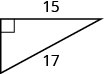
$Цифра являє собою прямокутний трикутник висотою 15 одиниць і гіпотенузою в 17 одиниць.$

54. Серхіо потрібно прикріпити провід для утримання антени до даху свого будинку, як показано на малюнку. Антена висотою вісім футів і Серхіо має 10 футів дроту. Як далеко від основи антени він може прикріпити провід? Приблизно до найближчої десятої, якщо це необхідно.

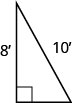
$Фігура являє собою прямокутний трикутник висотою 8 футів і гіпотенузою 10 футів.$

Відповідь: 6 футів

55. Сон будує стелажі в своєму гаражі. Полиці мають ширину 36 дюймів і 15 дюймів у висоту. Він хоче поставити діагональну дужку поперек спини, щоб стабілізувати полиці, як показано на малюнку. Як довго повинна бути дужка?

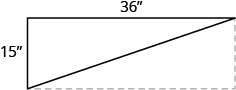
$На малюнку зображені прямокутні стелажі, ширина яких 36 дюймів і висота 15 дюймів утворюють прямокутний трикутник з діагональною скобою.$

56. Довжина прямокутника на 12 см більше ширини. Периметр 74 см. Знайдіть довжину і ширину.

Відповідь: $24.5$см,$12.5$ см

57. Ширина прямокутника на три більше, ніж в два рази більше довжини. Периметр - 96 дюймів. Знайдіть довжину і ширину.

58. Периметр трикутника становить 35 футів. Одна сторона трикутника на п'ять футів довша, ніж друга сторона. Третя сторона на три фути довше другої сторони. Знайдіть довжину кожної сторони.

Відповідь: 9 футів, 14 футів, 12 футів

Розв'язуйте суміші та рівномірні програми руху

Вирішити проблеми з монетним словом

У наступних вправах вирішуйте.

59. Полетт має $140 в $5 і $10 купюри. Кількість купюр у розмірі 10 доларів менше ніж удвічі перевищує кількість купюр у розмірі 5 доларів. Скільки у неї кожного?

60. Ленні має $3,69 в копійки, копійки, і чверті. Кількість копійок на три більше, ніж кількість копійок. Кількість чвертей в два рази перевищує кількість копійок. Скільки у нього кожної монети?

Відповідь: дев'ять копійок, шість копійок, 12 чверті

Вирішити проблеми з квитком і штампом Word

У наступних вправах вирішіть кожну проблему квитка або штампового слова.

61. Квитки на баскетбольний матч коштують 2 долари для студентів і 5 доларів для дорослих. Кількість учнів була втричі менше, ніж в 10 разів більше дорослих. Загальна сума грошей від продажу квитків склала 619 доларів. Скільки з кожного квитка було продано?

62. На концерт джаз-бенду було продано 125 квитків на загальну суму $1,022. Студентські квитки коштують $6 кожен, а загальні вхідні квитки коштують $10 кожен. Скільки з кожного виду квитків було продано?

Відповідь: 57 студентів, 68 дорослих

63. Юмі витратив 34,15 доларів на купівлю марок. Кількість марок у розмірі 0,56 долара, яку вона купила, була в 10 разів менше, ніж в чотири рази більше, ніж у 0,41 долара. Скільки з кожного вона купила?

Вирішити проблеми зі змішаними словами

У наступних вправах вирішуйте.

64. Маркіз робить 10 фунтів стежкової суміші з родзинок і горіхів. Ізюм коштує 3,45 долара за фунт, а горіхи коштують 7,95 доларів за фунт. Скільки фунтів родзинок і скільки фунтів горіхів повинен використовувати маркіз для суміші слідів, щоб коштувати йому $6,96 за фунт?

Відповідь: $2.2$фунтів родзинок,$7.8$ фунтів горіхів

65. Бурштиновий хоче покласти плитку на backsplash її кухонні лічильники. Їй знадобиться 36 квадратних футів плитки. Вона буде використовувати основні плитки, які коштують $8 за квадратний фут і декоратор плитки, які коштують $20 за квадратний фут. Скільки квадратних футів кожної плитки вона повинна використовувати так, що загальна вартість backsplash буде $10 за квадратний фут?

66. Енріке позичив 23 500 доларів на покупку автомобіля. Він платить дядькові 2% відсотків на $4500, які він позичив у нього, а банк платить 11,5% відсотків на решту. Яку середню процентну ставку він платить на загальну суму $23 500? (Округляйте відповідь до найближчої десятої частки відсотка.)

Відповідь: $9.7%$

Вирішити рівномірні програми руху

У наступних вправах вирішуйте.

67. Коли Гейб їздить з Сакраменто до Реддінга, він займає 2,2 години. Це займає Ельза дві години, щоб їздити на тій же відстані. Швидкість Ельзи на сім миль на годину швидше, ніж швидкість Гейба. Знайти швидкість Гейба і швидкість Ельзи 's.

68. Луеллен і Трейсі зустрілися в ресторані на дорозі між Чикаго і Нешвіллом. Луеллен виїхав з Чикаго і проїхав 3,2 години в напрямку Нешвілла. Трейсі залишила Нешвілл і їхала 4 години до Чикаго, зі швидкістю на одну милю на годину швидше, ніж швидкість Луеллена. Відстань між містами Чикаго та Нашвілл становить 472 км. Знайдіть швидкість Луеллена і швидкість Трейсі.

Відповідь: Швидкість 65 миль/год, Трейсі 66 миль/год

69. Два автобуси відправляються з Амарілло одночасно. Автобус Альбукерке прямує на захід на I-40 зі швидкістю 72 миль на годину, а автобус Оклахома-Сіті прямує на схід на I-40 зі швидкістю 78 миль на годину. Скільки годин знадобиться їм, щоб бути 375 миль один від одного?

70. Кайл гребв на човні вгору за течією протягом 50 хвилин. Йому знадобилося 30 хвилин, щоб повернутися вниз за течією. Його швидкість, що йде вгору за течією, на дві милі на годину повільніше, ніж його швидкість, що йде вниз за течією. Знайдіть швидкість Кайла вгору та нижче за течією.

Відповідь: вгору за течією 3 милі/год, нижче за течією 5

71. О 6:30 Девон покинув свій будинок і їхав на велосипеді по рівній дорозі до 7:30. Потім вона почала кататися в гору і їхала до 8:00. Вона проїхала в цілому 15 миль. Її швидкість на рівній дорозі була на три милі на годину швидше, ніж її швидкість, що йде в гору. Знайдіть швидкість Девона на рівній дорозі і їдьте в гору.

72. Ентоні проїхав з Нью-Йорка в Балтімор, який становить 192 милі. Він виїхав о 3:45 і мав інтенсивний рух до 5:30. Світлофор був легким для решти їзди, і він прибув о 7:30. Його швидкість в легкому русі становила чотири милі на годину більше ніж в два рази більше швидкості в інтенсивному русі. Знайдіть швидкість руху Ентоні в інтенсивному русі та легкому трафіку.

Відповідь: інтенсивний рух 32 миль/год, легкий трафік 66 миль/год

Вирішити лінійні нерівності

Нерівності графа на числовій лінії

У наступних вправах графік нерівності на числовому рядку і запишіть в інтервальні позначення.

73. $x<−1$

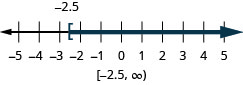
74. $x\geq −2.5$

Відповідь: $Розчин х більше або дорівнює від'ємним 2,5. Числовий рядок показує ліву дужку при негативному 2.5 із затіненням праворуч. Інтервальне позначення від'ємне від 2,5 до нескінченності в дужках і дужках.$

75. $x\leq \frac{5}{4}$

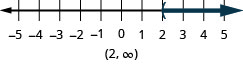
76. $x>2$

Відповідь: $Розчин х більше 2. Числовий рядок показує ліву дужку на 2 з затіненням праворуч. Інтервальне позначення дорівнює 2 до нескінченності в дужках.$

77. $−2<x<0$

78. $-5\leq x<−3$

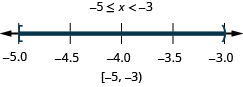
Відповідь: $Розв'язок негативний 5 менше або дорівнює x, який менше від'ємного 3. Числова лінія показує замкнуте коло при негативному 5, відкрите коло при негативному 3 та затінення між колами. Інтервальне позначення від'ємне від 5 до негативного 3 в дужках і дужках.$

79. $0\leq x\leq 3.5$

Вирішити лінійні нерівності

У наступних вправах розв'яжіть кожну нерівність, графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.

80. $n−12\leq 23$

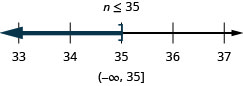
Відповідь: $Розчин n менше або дорівнює 35. Числова лінія показує праву дужку на 35 з затіненням ліворуч. Інтервальне позначення є негативною нескінченністю до 35 в дужках і дужках.$

81. $a+\frac{2}{3}\geq \frac{7}{12}$

82. $9x>54$

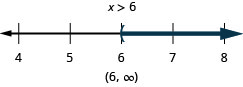
Відповідь: $Розчин х більше 6. Числовий рядок показує ліву дужку на позначці 6 із затіненням праворуч. Інтервальне позначення становить від 6 до нескінченності в дужках.$

83. $\frac{q}{−2}\geq −24$

84. $6p>15p−30$

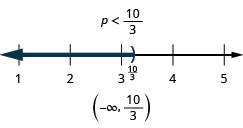
Відповідь: $Розчин р менше десяти третин. Числовий рядок показує праву дужку на десять третин із затіненням ліворуч. Інтервальне позначення є від'ємною нескінченністю до десяти третин в дужках.$

85. $9h−7(h−1)\leq 4h−23$

86. $5n−15(4−n)<10(n−6)+10n$

Відповідь: $Рішення - ідентичність. Його рішення на числовому рядку затінюється для всіх значень. Розв'язок у інтервальній нотації - негативна нескінченність до нескінченності в дужках.$

87. $\frac{3}{8}a−\frac{1}{12}a>\frac{5}{12}a+\frac{3}{4}$

Перекладіть слова на нерівність і вирішуйте

У наступних вправах перекладіть і вирішуйте. Потім запишіть рішення в інтервальних позначеннях і графі на числовому рядку.

88. На п'ять більше$z$, ніж максимум 19.

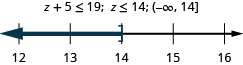
Відповідь: $Нерівність z плюс 5 менше або дорівнює 19. Його рішення z менше або дорівнює 14. Числова лінія показує праву дужку на 14 з затіненням ліворуч. Інтервальне позначення - це негативна нескінченність до 14 в дужках і дужці.$

89. Три менше, ніж$c$ це не менше 360.

90. У дев'ять разів$n$ перевищує 42.

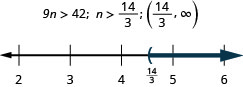
Відповідь: $Нерівність 9 n більше 42. Її розчин n більше чотирнадцяти третин. Числовий рядок показує ліві дужки на чотирнадцять третин із затіненням праворуч. Інтервальне позначення становить чотирнадцять третин до нескінченності в дужках.$

91. Негативних два рази$a$ - не більше восьми.

Розв'язуйте програми з лінійними нерівностями

У наступних вправах вирішуйте.

92. Джуліанна має щотижневий продовольчий бюджет у розмірі 231 доларів для своєї родини. Якщо вона планує бюджетувати однакову суму на кожен із семи днів тижня, яку максимальну суму вона може витрачати на їжу щодня?

Відповідь: $33 в день

93. Рохеліо фарбує аквареллю. Він отримав подарункову карту на 100 доларів до магазину художнього постачання і хоче використовувати її, щоб купити 12 ″ × 16 ″ полотен. Кожне полотно коштує $10,99. Яку максимальну кількість полотен він може придбати зі своєю подарунковою карткою?

94. Бріані запропонували роботу з продажу в іншому місті. Пропозиція склала 42 500 доларів плюс 8% від її загального обсягу продажів. Для того, щоб зробити це варто переїзду, Бріана повинна мати річну зарплату не менше 66 500 доларів. Що б її загальні продажі повинні бути для того, щоб вона переїхала?

Відповідь: не менше $300,000

95. Машина Рене коштує їй 195 доларів на місяць плюс $0.09 за милю. Скільки миль може проїхати Рене, щоб її щомісячні витрати на автомобіль становили не більше 250 доларів?

96. Коста - бухгалтер. Під час податкового сезону він стягує 125 доларів, щоб зробити просту податкову декларацію. Його витрати на покупку програмного забезпечення, оренду офісу, рекламу становлять $6000. Скільки податкових декларацій він повинен зробити, якщо хоче отримати прибуток не менше $8,000?

Відповідь: щонайменше 112 робочих місць

97. Дженна планує п'ятиденний курортний відпочинок з трьома своїми друзями. Це обійдеться їй у 279 доларів за авіаквитки, 300 доларів за їжу та розваги та 65 доларів на день за її частку готелю. Вона має $550 зекономлено на її відпустці і може заробляти $25 на годину як помічник у фотостудії свого дядька. Скільки годин вона повинна працювати, щоб вистачило грошей на відпустку?

Вирішити складні нерівності

Вирішити складні нерівності за допомогою «і»

У кожному з наступних вправ розв'яжіть кожну нерівність, графуйте рішення та запишіть рішення в інтервальних позначеннях.

98. $x\leq 5$і$x>−3$

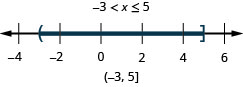
Відповідь: $Розв'язок негативний 3 менше x, який менше або дорівнює 5. Числова лінія показує відкрите коло при негативному 3 і замкнуте коло на 5. Інтервальне позначення від'ємне від 3 до 5 в дужках і дужках.$

99. $4x−2\leq 4$і$7x−1>−8$

100. $5(3x−2)\leq 5$і$4(x+2)<3$

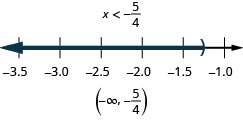
Відповідь: $Розв'язок від'ємний х менше від'ємних п'яти четвертих. Числова лінія показує відкрите коло на від'ємних п'яти четвертих із затіненням ліворуч. Інтервальне позначення - негативна нескінченність до негативних п'яти четвертих в дужках.$

101. $34(x−8)\leq 3$і$15(x−5)\leq 3$

102. $34x−5\geq −2$і$−3(x+1)\geq 6$

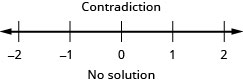
Відповідь: $Рішення - протиріччя. Отже, рішення немає. В результаті на числовому рядку або інтервальних позначеннях немає графіка.$

103. $−5\leq 4x−1<7$

Вирішити складні нерівності за допомогою «або»

104. $5−2x\leq −1$або$6+3x\leq 4$

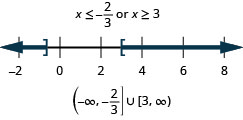
Відповідь: $Розв'язок х менше від'ємних двох третин або х більше або дорівнює 3. Числова лінія показує замкнуте коло на від'ємні дві третини з затіненням ліворуч і замкнуте коло на 3 з затіненням праворуч. Інтервальне позначення - це об'єднання негативної нескінченності до негативних двох третин у дужках та дужці та 3 до нескінченності в дужці та дужках.$

105. $3(2x−3)<−5$або$4x−1>3$

106. $34x−2>4$або$4(2−x)>0$

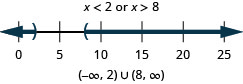
Відповідь: $Розчин х менше 2 або х більше 8. Числова лінія показує відкрите коло на 2 з затіненням ліворуч і відкрите коло на 8 із затіненням праворуч. Інтервальне позначення - це об'єднання негативної нескінченності до 8 в дужках і 8 до нескінченності в дужках.$

107. $2(x+3)\geq 0$або$3(x+4)\leq 6$

108. $12x−3\leq 4$або$13(x−6)\geq −2$

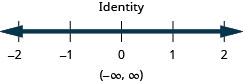
Відповідь: $Рішення - ідентичність. Його рішення на числовому рядку затінюється для всіх значень. Розв'язок у інтервальній нотації - негативна нескінченність до нескінченності в дужках.$

Розв'язуйте програми зі складними нерівностями

У наступних вправах вирішуйте.

109. Ліам грає номер гри зі своєю сестрою Одрі. Ліам думає про число і хоче, щоб Одрі здогадалася. У п'ять більше трьох разів її число становить від 2 до 32. Напишіть складну нерівність, яка показує діапазон чисел, про які може думати Ліам.

110. Elouise створює прямокутний сад у своєму задньому дворі. Довжина саду становить 12 футів. Периметр саду повинен бути не менше 36 футів і не більше 48 футів. Використовуйте складну нерівність, щоб знайти діапазон значень ширини саду.

Відповідь: $6\leq w\leq 12$

Вирішити нерівності абсолютних значень

Вирішити рівняння абсолютного значення

У наступних вправах вирішуйте.

111. $|x|=8$

112. $|y|=−14$

Відповідь: немає рішення

113. $|z|=0$

114. $|3x−4|+5=7$

Відповідь: $x=2,x=\frac{2}{3}$

115. $4|x−1|+2=10$

116. $−2|x−3|+8=−4$

Відповідь: $x=9,x=−3$

117. $|12x+5|+4=1$

118. $|6x−5|=|2x+3|$

Відповідь: $x=2,x=14$

Розв'яжіть нерівності абсолютних значень з «менше ніж»

У наступних вправах вирішуйте кожну нерівність. Графік розв'язку і запишіть рішення в інтервальні позначення.

119. $|x|\leq 8$

120. $|2x−5|\leq 3$

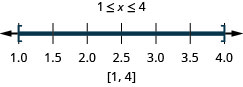
Відповідь: $Розчин 1 менше або дорівнює х, який менше або дорівнює 4. Числова лінія показує замкнуте коло в 1, замкнуте коло на 4, і затінення між колами. Інтервальне позначення становить від 1 до 4 в дужках.$

121. $|6x−5|<7$

122. $|5x+1|\leq −2$

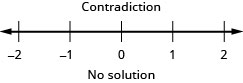
Відповідь: $Рішення - протиріччя. Отже, рішення немає. В результаті немає графіка або числового рядка або інтервалу позначення.$

Розв'яжіть нерівності абсолютних значень з «більше ніж»

У наступних вправах вирішуйте. Графік розв'язку і запишіть рішення в інтервальні позначення.

123. $|x|>6$

124. $|x|\geq 2$

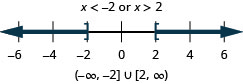
Відповідь: $Рішення х менше від'ємного 2 або х більше 6. Числова лінія показує замкнуте коло при негативному 2 з затіненням ліворуч і замкнуте коло на 2 з затіненням праворуч. Інтервальне позначення - це об'єднання негативної нескінченності до негативної 2 в дужках і дужці та 2 до нескінченності в дужці та дужках.$

125. $|x−5|>−2$

126. $|x−7|\geq 1$

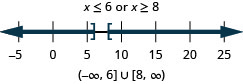
Відповідь: $Розчин х менше або дорівнює 6 або х більше або дорівнює 8. Числова лінія показує замкнуте коло на 6 з затіненням ліворуч і замкнуте коло на 8 з затіненням праворуч. Інтервальне позначення - це об'єднання негативної нескінченності до негативної 6 у дужках та дужці та 8 до нескінченності в дужці та дужках.$

127. $3|x|+4\geq 1$

Вирішуйте програми з абсолютним значенням

У наступних вправах вирішуйте.

128. Крафтовий пивовар потребує 215 000 пляшок на день. Але ця загальна сума може варіюватися на цілих 5000 пляшок. Яке максимальне та мінімальне очікуване використання на підприємстві з розливу?

Відповідь: Мінімальне та максимальне очікуване використання становить від 210 000 до 220 000 пляшок.

129. У Fancy Grocery ідеальна вага буханки хліба становить 16 унцій. Згідно із законом фактична вага може варіюватися від ідеалу на 1,5 унції. Який діапазон ваги буде прийнятним для інспектора, не викликаючи оштрафування хлібопекарні?

Практичний тест

У наступних вправах розв'яжіть кожне рівняння.

1. $−5(2x+1)=45$

Відповідь: $x=−5$

2. $\frac{1}{4}(12m+28)=6+2(3m+1)$

3. $8(3a+5)−7(4a−3)=20−3a$

Відповідь: $a=41$

4. $0.1d+0.25(d+8)=4.1$

5. $14n−3(4n+5)=−9+2(n−8) $

Відповідь: протиріччя; немає рішення

6. $3(3u+2)+4[6−8(u−1)]=3(u−2)$

7. $\frac{3}{4}x−\frac{2}{3}=\frac{1}{2}x+\frac{5}{6}$

Відповідь: $x=6$

8. $|3x−4|=8$

9. $|2x−1|=|4x+3|$

Відповідь: $x=−2,x=−13$

10. Розв'яжіть формулу
$x+2y=5$ для y.

У наступних вправах графік нерівності на числовому рядку і запишіть в інтервальні позначення.

11. $x\geq −3.5$

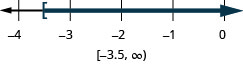
Відповідь: $Нерівність x більше або дорівнює від'ємним 3.5. Числовий рядок показує ліву дужку з від'ємним 3.5 і затінення праворуч. Інтервальне позначення від'ємне від 3,5 до нескінченності в дужках і дужках.$

12. $x<\frac{11}{4}$

13. $−2\leq x<5$

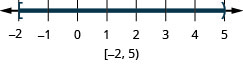
Відповідь: $Нерівність від'ємна два менше або дорівнює x, що менше 5. Числова лінія показує замкнуте коло при негативному 2 і відкрите коло на 5 із затіненням між колами. Інтервальне позначення від'ємне від 2 до 5 в дужках і дужках.$

14. $8k\geq 5k−120$

15. $3c−10(c−2)<5c+16$

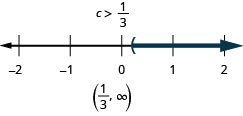
Відповідь: $Розчин з більше однієї третини. Числовий рядок показує ліву дужку на третині з затіненням праворуч. Інтервальне позначення дорівнює третині до нескінченності в дужках.$

16. $\frac{3}{4}x−5\geq −2$і$−3(x+1)\geq 6$

17. $3(2x−3)<−5$або$4x−1>3$

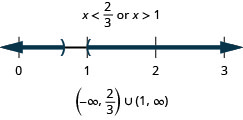
Відповідь: $Розчин х менше двох третин або х більше 1. Числова лінія показує відкрите коло на дві третини із затіненням ліворуч та відкрите коло на 1 із затіненням праворуч. Інтервальне позначення - це об'єднання негативної нескінченності до двох третин в дужках і від 1 до нескінченності в дужках.$

18. $\frac{1}{2}x−3\leq 4$або$\frac{1}{3}(x−6)\geq −2$

19. $|4x−3|\geq 5$

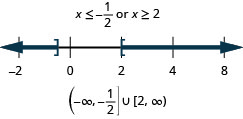
Відповідь: $Розв'язок x менше або дорівнює від'ємній половині або х більше або дорівнює 2. Числова лінія показує замкнуте коло на від'ємній половині з затіненням ліворуч і замкнуте коло на 2 з затіненням праворуч. Інтервальне позначення - це об'єднання негативної нескінченності до негативної половини в дужках і дужках і 2 до нескінченності в дужках і дужках.$

У наступних вправах перевести на рівняння або нерівність і вирішити.

20. Чотири менше ніж в два рази х дорівнює 16.

21. Знайдіть довжину відсутньої сторони.

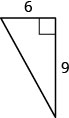
$Фігура являє собою прямокутний трикутник з основою в 6 одиниць і висотою 9 одиниць.$

Відповідь: $10.8$

22. Одне число - це чотири більше, ніж в два рази інше. Їх сума є$−47$. Знайдіть цифри.

23. Сума двох послідовних непарних цілих чисел дорівнює$−112$. Знайдіть цифри.

Відповідь: $−57,−55$

24. Маркус купив телевізор у продажу за 626,50 доларів. Початкова ціна телевізора становила 895 доларів. Знайти ⓐ суму знижки і ⓑ ставку дисконту.

25. Боніта має $2,95 в копійках і чвертях в кишені. Якщо у неї на п'ять копійок більше чвертей, скільки у неї кожної монети?

Відповідь: 12 даймів, сім чвертей

26. Кім робить вісім галонів пуншу з фруктового соку і соди. Фруктовий сік коштує $6,04 за галон, а сода коштує $4,28 за галон. Скільки фруктового соку і скільки соди вона повинна використовувати, щоб удар коштував $5,71 за галон?

27. Міра одного кута трикутника вдвічі перевищує міру найменшого кута. Міра третього кута втричі перевищує міру найменшого кута. Знайдіть мірки всіх трьох кутів.

Відповідь: $30°,60°,90°$

28. Довжина прямокутника на п'ять футів більше, ніж в чотири рази більше ширини. Периметр - 60 футів. Знайдіть розміри прямокутника.

29. Два літаки залишають Даллас одночасно. Один прямує на схід зі швидкістю 428 миль на годину. Інший літак прямує на захід зі швидкістю 382 милі на годину. Скільки годин знадобиться їм, щоб бути 2,025 миль один від одного?

Відповідь: $2.5$годин

30. Леон поїхав зі свого будинку в Цинциннаті до будинку своєї сестри в Клівленді, відстань 252 миль. Це зайняло у нього$4\frac{1}{2}$ години. Перші півгодини він мав інтенсивний рух, а решту часу його швидкість становила п'ять миль на годину менше, ніж в два рази більше швидкості в інтенсивному русі. Якою була його швидкість в інтенсивному русі?

31. Сара має бюджет у розмірі 1000 доларів на костюми для 18 членів її музичного театрального колективу. Який максимум вона може витратити на кожен костюм?

Відповідь: Не більше $55.56 за костюм.