2.8: Вирішити нерівності абсолютних значень
- Page ID
- 59780
До кінця цього розділу ви зможете:
- Вирішити абсолютні рівняння
- Вирішити нерівності абсолютних значень з «менше ніж»
- Вирішити нерівності абсолютних значень з «більше ніж»
- Вирішуйте програми з абсолютним значенням
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Оцініть:\(−|7|\).
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Заповніть\(<,>,<,>,\) або\(=\) для кожної з наступних пар чисел.
ⓐ\(|−8|\text{___}−|−8|\) ⓑ\(12\text{___}−|−12|\) ⓒ\(|−6|\text{___}−6\) ⓓ\(−(−15)\text{___}−|−15|\)
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Спростити:\(14−2|8−3(4−1)|\).
Якщо ви пропустили цю проблему, перегляньте [посилання].
Вирішити рівняння абсолютного значення
Готуючись до вирішення рівнянь абсолютних значень, ми переглядаємо наше визначення абсолютної величини.
Абсолютне значення числа - це його відстань від нуля на числовому рядку.
Абсолютне значення числа n записується як\(|n|\) і\(|n|\geq 0\) для всіх чисел.
Абсолютні значення завжди більше або рівні нулю.
Ми дізналися, що і число, і його протилежність - це однакова відстань від нуля на числовій лінії. Так як вони мають однакову відстань від нуля, вони мають однакове абсолютне значення. Наприклад:
- \(−5\)це 5 одиниць від 0, так що\(|−5|=5\).
- \(5\)це 5 одиниць від 0, так що\(|5|=5\).
Малюнок\(\PageIndex{1}\) ілюструє цю ідею.
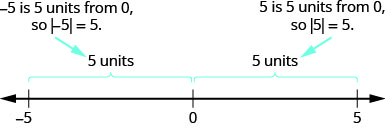
Для рівняння |x|=5, |x|=5 ми шукаємо всі числа, які роблять це твердження істинним. Шукаємо числа, відстань яких від нуля дорівнює 5. Ми щойно побачили, що і 5, і −5−5 — це п'ять одиниць від нуля на числовому рядку. Вони є розв'язками рівняння.
\(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\)
Рішення можна спростити до єдиного твердження шляхом написання\(x=\pm 5\). Це читається: «х дорівнює позитивному або негативному 5».
Ми можемо узагальнити це до наступної властивості для рівнянь абсолютного значення.
Для будь-якого алгебраїчного виразу, u та будь-якого позитивного дійсного числа, a,
\[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\]
Пам'ятайте, що абсолютне значення не може бути від'ємним числом.
Вирішити:
- \(|x|=8\)
- \(|y|=−6\)
- \(|z|=0\)
- Рішення a
-
\(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pm 8} \\ \end{array}\)
- Рішення б
-
\(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\)
Оскільки абсолютне значення завжди позитивне, розв'язків цього рівняння немає. - Рішення c
-
\(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\)
Обидва рівняння говорять нам, що z=0z=0 і тому існує лише одне рішення.
Вирішити:
- \(|x|=2\)
- \(|y|=−4\)
- \(|z|=0\)
- Відповідь
-
\(\pm 2\)
- Відповідь б
-
немає рішення
- Відповідь c
-
0
Вирішити:
- \(|x|=11\)
- \(|y|=−5\)
- \(|z|=0\)
- Відповідь
-
\(\pm 11\)
- Відповідь б
-
немає рішення
- Відповідь c
-
0
Щоб розв'язати рівняння абсолютних значень, ми спочатку ізолюємо вираз абсолютного значення, використовуючи ті самі процедури, які ми використовували для розв'язання лінійних рівнянь. Як тільки ми виділимо вираз абсолютного значення, ми перепишемо його як два еквівалентні рівняння.
Як розв'язати рівняння абсолютних значень
Вирішити\(|5x−4|−3=8\).
- Рішення
-




Вирішити:\(|3x−5|−1=6\).
- Відповідь
-
\(x=4, \space x=−\frac{2}{3}\)
Вирішити:\(|4x−3|−5=2\).
- Відповідь
-
\(x=−1,\space x=\frac{5}{2}\)
Кроки розв'язання рівняння абсолютного значення підсумовуються тут.
- Виділити вираз абсолютного значення.
- Напишіть еквівалентні рівняння.
- Вирішіть кожне рівняння.
- Перевірте кожне рішення.
Вирішити\(2|x−7|+5=9\).
- Рішення
-
\(2|x−7|+5=9\) Виділити вираз абсолютного значення. \(2|x−7|=4\) \(|x−7|=2\) Напишіть еквівалентні рівняння. \(x−7=−2\)або\(x−7=2\) Вирішіть кожне рівняння. \(x=5\)або\(x=9\) Перевірка:
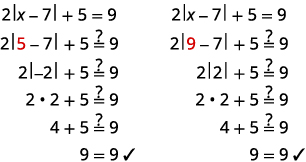
Вирішити:\(3|x−4|−4=8\).
- Відповідь
-
\(x=8,\space x=0\)
Вирішити:\(2|x−5|+3=9\).
- Відповідь
-
\(x=8,\space x=2\)
Пам'ятайте, абсолютне значення завжди позитивне!
Вирішити:\(|\frac{2}{3}x−4|+11=3\).
- Рішення
-
\(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\)
Вирішити:\(|\frac{3}{4}x−5|+9=4\).
- Відповідь
-
Немає рішення
Вирішити:\(|\frac{5}{6}x+3|+8=6\).
- Відповідь
-
Немає рішення
Деякі з наших рівнянь абсолютних значень можуть мати вигляд,\(|u|=|v|\) де u і v - алгебраїчні вирази. Наприклад,\(|x−3|=|2x+1|\).
Як би ми їх вирішували? Якщо два алгебраїчних вирази рівні за абсолютним значенням, то вони або рівні один одному, або негативи один одного. Властивість рівнянь абсолютних значень говорить, що для будь-якого алгебраїчного виразу, u, і додатне дійсне число, a, if\(|u|=a\), то\(u=−a\) або\(u=a\).
Це говорить нам, що
\ (\ begin {масив}
{llll} {\ текст {якщо}} & {|u|u|=|v|} & {}
\\ {\ текст {потім}} & {|u|=v} & {\ текст {або}} & {|u||=−v}
\\ {\ текст {і так}} & {u=v\ text {або} u = −v} & {\ текст {або}} & {u=−v\ text {or} u = − (−v)}
\\ end {масив}\)
Це призводить нас до наступного властивості для рівнянь з двома абсолютними значеннями.
Для будь-яких алгебраїчних виразів u і v,
\[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\]
Коли ми беремо протилежне кількості, ми повинні бути обережними зі знаками та додавати дужки там, де це необхідно.
Вирішити:\(|5x−1|=|2x+3|\).
- Рішення
-
\(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\)
Вирішити:\(|7x−3|=|3x+7|\).
- Відповідь
-
\(x=−\frac{2}{5}, \space x=\frac{5}{2}\)
Вирішити:\(|6x−5|=|3x+4|\).
- Відповідь
-
\(x=3, x=19\)
Розв'яжіть нерівності абсолютних значень за допомогою «Менше ніж»
Давайте тепер розглянемо, що відбувається, коли ми маємо абсолютну величину нерівності. Все, що ми дізналися про вирішення нерівностей, все ще залишається, але ми повинні враховувати, як абсолютна цінність впливає на нашу роботу. Знову розглянемо наше визначення абсолютної величини. Абсолютне значення числа - це його відстань від нуля на числовому рядку. Для рівняння ми побачили\(|x|=5\), що обидва 5 і\(−5\) п'ять одиниць від нуля на числовій лінії. Вони є розв'язками рівняння.
\[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]
А як щодо нерівності\(|x|\leq 5\)? Де знаходяться числа, відстань яких менше або дорівнює 5? Ми знаємо,\(−5\) і 5 - це обидва п'ять одиниць з нуля. Всі числа між\(−5\) і 5 менше п'яти одиниць з нуля (рис.\(\PageIndex{2}\)).
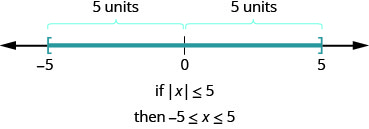
У більш загальному вигляді ми можемо побачити, що якщо\(|u|\leq a\), то\(−a\leq u\leq a\) (рис.\(\PageIndex{3}\)).
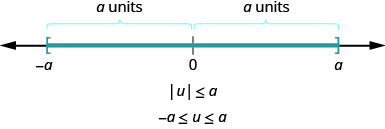
Цей результат підсумований тут.
Для будь-якого алгебраїчного виразу, u та будь-якого позитивного дійсного числа, a,
\[ \text{if} \quad |u|<a, \quad \text{then} \space −a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space−a\leq u\leq a \nonumber\]
Після вирішення нерівності часто корисно перевірити деякі моменти, щоб побачити, чи має рішення сенс. Графік розв'язку ділить числову лінію на три ділянки. Виберіть значення в кожному розділі та підставляйте його у вихідну нерівність, щоб побачити, чи робить це нерівність істинною чи ні. Хоча це не повна перевірка, вона часто допомагає перевірити рішення.
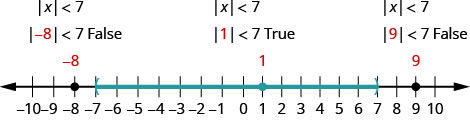
Вирішити\(|x|<7\). Графік розв'язку і запишіть рішення в інтервальне позначення.
- Рішення
-
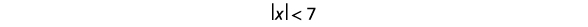
Запишіть еквівалентну нерівність. 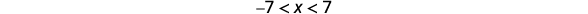
Графік рішення. 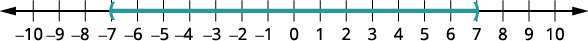
Запишіть рішення, використовуючи інтервальні позначення. 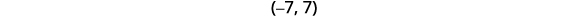
Перевірка:
Щоб перевірити, перевірте значення в кожному розділі числового рядка, що показує рішення. Виберіть такі числа, як −8, −8, 1 та 9.
Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(|x|<9\).
- Відповідь
-
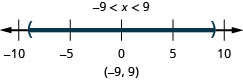
Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(|x|<1\).
- Відповідь
-
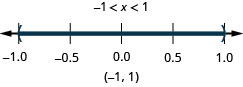
Вирішити\(|5x−6|\leq 4\). Графік розв'язку і запишіть рішення в інтервальне позначення.
- Рішення
-
Крок 1. Виділити вираз абсолютного значення.
Вона ізольована.\(|5x−6|\leq 4\) Крок 2. Запишіть еквівалентну складну нерівність. \(−4\leq 5x−6\leq 4\) Крок 3. Розв'яжіть складну нерівність. \(2\leq 5x\leq 10\)
\(\frac{2}{5}\leq x\leq 2\)Крок 4. Графік рішення. 
Крок 5. Запишіть рішення, використовуючи інтервальні позначення. \([\frac{2}{5}, 2]\)
Перевірка: чек залишений вам.
Вирішити\(|2x−1|\leq 5\). Графік розв'язку і запишіть рішення в інтервальне позначення:
- Відповідь
-
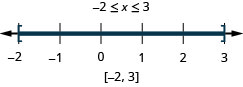
Вирішити\(|4x−5|\leq 3\). Графік розв'язку і запишіть рішення в інтервальне позначення:
- Відповідь
-
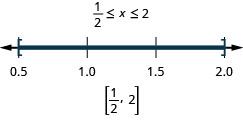
- Виділити вираз абсолютного значення.
- Запишіть еквівалентну складну нерівність.
\[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{−a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{−a\leq u\leq a} \\ \nonumber \end{array}\]
- Вирішити складну нерівність.
- Графік рішення
- Запишіть рішення, використовуючи інтервальні позначення.
Розв'яжіть нерівності абсолютних значень за допомогою «Більше ніж»
Що відбувається з абсолютними ціннісними нерівностями, які мають «більше, ніж»? Знову розглянемо наше визначення абсолютної величини. Абсолютне значення числа - це його відстань від нуля на числовому рядку.
Ми почали з нерівності\(|x|\leq 5\). Ми побачили, що числа, відстань яких менше або дорівнює п'яти від нуля на числовій лінії були\(−5\) і 5 і всі числа між\(−5\) і 5 (рис.\(\PageIndex{4}\)).
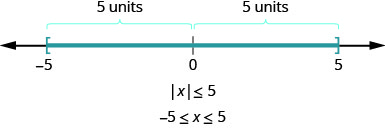
Тепер ми хочемо подивитися на нерівність\(|x|\geq 5\). Де знаходяться числа, відстань яких від нуля більше або дорівнює п'яти?
Знову обидва\(−5\) і 5 - це п'ять одиниць з нуля і так включені в розчин. Числа, відстань яких від нуля більше п'яти одиниць, були б менше\(−5\) і більше 5 на числовому рядку (рис.\(\PageIndex{5}\)).
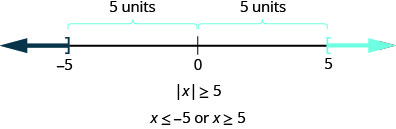
У більш загальному вигляді ми можемо побачити, що якщо\(|u|\geq a\), то\(u\leq −a\) або\(u\leq a\). Див. Малюнок.
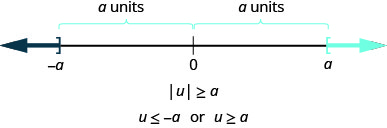
Цей результат підсумований тут.
Для будь-якого алгебраїчного виразу, u та будь-якого позитивного дійсного числа, a,
\[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<−a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq −a \text{ or } u\geq a} \\ \nonumber \end{array}\]
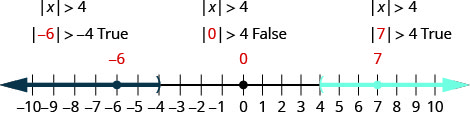
Вирішити\(|x|>4\). Графік розв'язку і запишіть рішення в інтервальне позначення.
- Рішення
-
\(|x|>4\) Запишіть еквівалентну нерівність. \(x<−4\)або\(x>4\) Графік рішення. 
Запишіть рішення, використовуючи інтервальні позначення. \((−\inf ,−4)\cup (4,\inf )\) Перевірка: Щоб перевірити, перевірте значення в кожному розділі числового рядка, що показує рішення. Виберіть такі числа, як −6, −6, 0 та 7.
Вирішити\(|x|>2\). Графік розв'язку і запишіть рішення в інтервальне позначення.
- Відповідь
-
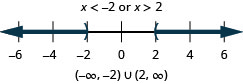
Вирішити\(|x|>1\). Графік розв'язку і запишіть рішення в інтервальне позначення.
- Відповідь
-
Вирішити\(|2x−3|\geq 5\). Графік розв'язку і запишіть рішення в інтервальне позначення.
- Рішення
-
\(|2x−3|\geq 5\) Крок 1. Виділити вираз абсолютного значення. Вона ізольована. Крок 2. Запишіть еквівалентну складну нерівність. \(2x−3\leq −5\)або\(2x−3\geq 5\) Крок 3. Розв'яжіть складну нерівність. \(2x\leq −2\)або\(2x\geq 8\)
\(x\leq −1\) або\(x\geq 4\)Крок 4. Графік рішення. 
Крок 5. Запишіть рішення, використовуючи інтервальні позначення. \((−\inf ,−1]\cup [4,\inf )\)
Перевірка: чек залишений вам.
Вирішити\(|4x−3|\geq 5\). Графік розв'язку і запишіть рішення в інтервальне позначення.
- Відповідь
-
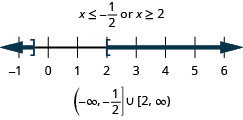
Вирішити\(|3x−4|\geq 2\). Графік розв'язку і запишіть рішення в інтервальне позначення.
- Відповідь
-
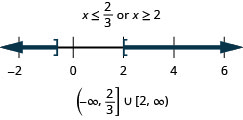
- Виділити вираз абсолютного значення.
- Запишіть еквівалентну складну нерівність.
\ [\ begin {масив} {lll}
{|u| >a} & {\ quad\ текст {еквівалентно}} & {u<−a\ quad\ text {або}\ quad u>a}
\\ {|u|\ geq a} & {\ quad\ text {еквівалентно}}} & {u\ leq −a\ quad\ text {або}\ quad u\ geq a}
\\ {|u| >a} & {\ quad\ text {еквівалентно}} & {u<−a\ quad\ text {або}\ quad u>a}
\\ {|u|\ geq a} & {\ quad\ text {еквівалентно}}} & {u\ leq −a\ quad\ text {або}\ quad u
\ geq a} nonumber\ end {масив}\] - Вирішити складну нерівність.
- Графік рішення
- Запишіть рішення, використовуючи інтервальні позначення.
Вирішуйте програми з абсолютним значенням
Абсолютні величини нерівності часто використовуються в процесі виготовлення. Елемент повинен бути виготовлений з майже ідеальними характеристиками. Зазвичай існує певний допуск відмінності від технічних характеристик, що допускається. Якщо відмінність від специфікацій перевищує допуск, деталь відхиляється.
\[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]
Ідеальний діаметр стрижня, необхідного для верстата, становить 60 мм. Фактичний діаметр може варіюватися від ідеального діаметра на\(0.075\) мм. Який діапазон діаметрів буде прийнятним для замовника, не викликаючи відхилення стрижня?
- Рішення
-
\(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x−60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{−0.075\leq x−60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 mm \text{ and } 60.075 mm.} \\ \end{array}\)
Ідеальний діаметр стрижня, необхідного для верстата, становить 80 мм. Фактичний діаметр може варіюватися від ідеального діаметра на 0,009 мм. Який діапазон діаметрів буде прийнятним для замовника, не викликаючи відхилення стрижня?
- Відповідь
-
Діаметр стрижня може бути в межах від 79,991 до 80,009 мм.
Ідеальний діаметр стрижня, необхідного для верстата, становить 75 мм. Фактичний діаметр може варіюватися від ідеального діаметра на 0,05 мм. Який діапазон діаметрів буде прийнятним для замовника, не викликаючи відхилення стрижня?
- Відповідь
-
Діаметр стрижня може бути в межах 74,95 і 75,05 мм.
Отримайте доступ до цього онлайн-ресурсу для отримання додаткових інструкцій та практики з розв'язуванням лінійних абсолютних рівнянь та нерівностей.
- Розв'язування лінійних абсолютних рівнянь та нерівностей
Ключові концепції
- Абсолютне значення
. Абсолютне значення числа - це його відстань від 0 на числовому рядку.
Абсолютне значення числа n записується як\(|n|\) і\(|n|\geq 0\) для всіх чисел.
Абсолютні значення завжди більше або рівні нулю. - Рівняння абсолютних
значень Для будь-якого алгебраїчного виразу, u та будь-якого додатного дійсного числа, a,
\(\begin{array} {ll} {\text{if}} &{\quad |u|=a} \\ {\text{then}} &{\quad u=−a \text{ or } u=a} \\ \end{array}\)
Пам'ятайте, що абсолютне значення не може бути від'ємним числом. - Як вирішити рівняння абсолютних значень
- Виділити вираз абсолютного значення.
- Напишіть еквівалентні рівняння.
- Вирішіть кожне рівняння.
- Перевірте кожне рішення.
- Рівняння з двома абсолютними значеннями
Для будь-яких алгебраїчних виразів u і v,
\(\begin{array} {ll} {\text{if}} &{\quad |u|=|v|} \\ {\text{then}} &{\quad u=−v \text{ or } u=v} \\ \end{array}\) - Нерівності абсолютних значень з будь-яким алгебраїчним виразом\(<\) або\(\leq\)
Для будь-якого алгебраїчного виразу, u та будь-яке додатне дійсне число, a,
\(\begin{array} {llll} {\text{if}} &{\quad |u|=a} &{\quad \text{then}} &{−a<u<a} \\ {\text{if}} &{\quad |u|\leq a} &{\quad \text{then}} &{−a\leq u\leq a} \\ \end{array}\) - Як вирішити нерівності абсолютних значень за допомогою\(<\) або\(\leq\)
- Виділити вираз абсолютного значення.
- Запишіть еквівалентну складну нерівність.
\(\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{\quad −a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{\quad −a\leq u\leq a} \\ \end{array}\) - Вирішити складну нерівність.
- Графік рішення
- Запишіть рішення, використовуючи інтервальні позначення
- Нерівності абсолютних значень з будь-яким алгебраїчним виразом\(>\) або\(\geq\)
Для будь-якого алгебраїчного виразу, u та будь-яке додатне дійсне число, a,
\(\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\text{then } u<−a\text{ or }u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\text{then } u\leq −a\text{ or }u\geq a} \\ \end{array}\) - Як вирішити нерівності абсолютних значень за допомогою\(>\) або\(\geq\)
- Виділити вираз абсолютного значення.
- Запишіть еквівалентну складну нерівність.
\(\begin{array} {lll} {|u|>a} &{\quad \text{is equivalent to}} &{\quad u<−a\text{ or }u>a} \\ {|u|\geq a} &{\quad \text{is equivalent to}} &{\quad u\leq −a\text{ or }u\geq a} \\ \end{array}\) - Вирішити складну нерівність.
- Графік рішення
- Запишіть рішення, використовуючи інтервальні позначення
