Skip to main content
LibreTexts - Ukrayinska

2.7: Вирішити складні нерівності

  1. Last updated
  2. Save as PDF
  • Page ID
    59796

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Вирішити складні нерівності за допомогою «і»
    • Вирішити складні нерівності за допомогою «або»
    • Розв'язуйте програми зі складними нерівностями

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Спростити:\(\frac{2}{5}(x+10)\).
      Якщо ви пропустили цю проблему, перегляньте [посилання].
    2. Спростити:\(−(x−4)\).
      Якщо ви пропустили цю проблему, перегляньте [посилання].

    Вирішити складні нерівності за допомогою «і»

    Тепер, коли ми знаємо, як вирішити лінійні нерівності, наступним кроком є погляд на складні нерівності. Складна нерівність складається з двох нерівностей, пов'язаних словом «і» або словом «або». Наприклад, нижче наведені складні нерівності.

    \[\begin{array} {lll} {x+3>−4} &{\text{and}} &{4x−5\leq 3} \\ {2(y+1)<0} &{\text{or}} &{y−5\geq −2} \\ \end{array} \nonumber\]

    СКЛАДНА НЕРІВНІСТЬ

    Складна нерівність складається з двох нерівностей, пов'язаних словом «і» або словом «або».

    Вирішити складну нерівність означає знайти всі значення змінної, які роблять складну нерівність істинним твердженням. Розв'язуємо складні нерівності, використовуючи ті самі методи, які ми використовували для розв'язання лінійних нерівностей. Розв'язуємо кожну нерівність окремо, а потім розглянемо два розв'язки.

    Щоб вирішити складну нерівність словом «і», ми шукаємо всі числа, які роблять обидві нерівності істинними. Щоб вирішити складну нерівність словом «або», ми шукаємо всі числа, які роблять нерівність істинною.

    Почнемо з складених нерівностей з «і». Нашим рішенням будуть числа, які є розв'язками обох нерівностей, відомих як перетин двох нерівностей. Розглянемо перехрестя двох вулиць—частина, де перекриваються вулиці—належить обом вулицям.

    Малюнок являє собою ілюстрацію двох вулиць з затіненим їх перетином

    Щоб знайти рішення складної нерівності «і», ми розглянемо графіки кожної нерівності, а потім знаходимо числа, які належать обом графікам - де графіки перекриваються.

    Для складної нерівності\(x>−3\) і\(x\leq 2\), ми графуємо кожну нерівність. Потім шукаємо, де графіки «перекриваються». Числа, які затінені на обох графіках, будуть затінені на графіку розв'язку складної нерівності. Див\(\PageIndex{1}\). Малюнок.

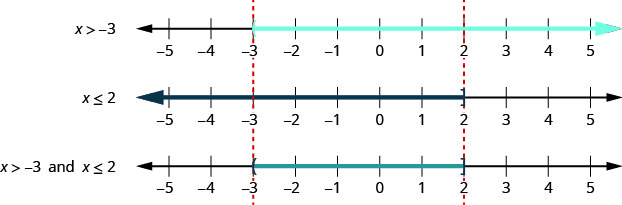
    На малюнку показано графік x більше негативного 3 з лівою дужкою при негативній 3 і затіненням праворуч, графік x менше або дорівнює 2 з дужкою в 2 і затіненням ліворуч, а графік x більше негативного 3 і x менше або дорівнює 2 з лівою дужкою при негативних 3 і правій дужці в 2 і затінення між негативними 3 і 2. Негативні 3 і 2 позначені рядками на кожному числовому рядку.
    Малюнок\(\PageIndex{1}\)

    Ми бачимо, що числа між\(−3\) і\(2\) затінені на обох перших двох графіках. Потім вони будуть затінені на графіку рішення.

    Число\(−3\) не затінено на першому графіку, тому, оскільки воно не затінено на обох графіках, воно не включається до графіка рішення.

    Число два затінено як на першому, так і на другому графіках. Тому він буде затінений на графіку рішення.

    Ось як ми покажемо наше рішення в наступних прикладах.

    Приклад\(\PageIndex{1}\)

    Вирішити\(6x−3<9\) і\(2x+7\geq 3\). Графік розв'язку і запишіть рішення в інтервальне позначення.

    Відповідь
      \(6x−3<9\) і \(2x+9\geq 3\)
    Крок 1. Вирішити кожну
    нерівність.    		 \(6x−3<9\)   \(2x+9\geq 3\)
      \(6x<12\)   \(2x\geq −6\)
      \(x<2\) і \(x\geq −3\)
    Крок 2. Графік кожного рішення. Потім графуйте числа, які роблять обидві нерівності істинними. Остаточний графік покаже всі числа, які роблять обидві нерівності істинними - числа, затінені на обох перших двох графіках. .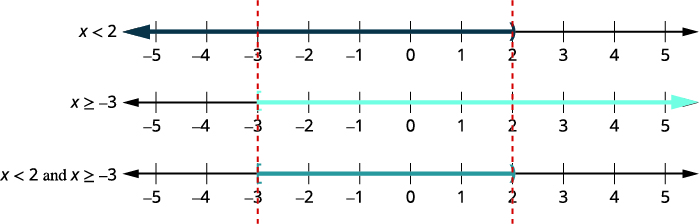
    Крок 3. Запишіть рішення в інтервальних позначеннях. \([−3,2)\)
    Усі числа, які роблять обидві нерівності істинними, є рішенням складної нерівності.
    Приклад\(\PageIndex{2}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(4x−7<9\) і\(5x+8\geq 3\).

    Відповідь

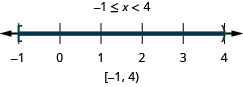
    Розв'язок негативний 1 менше або дорівнює x, який менше 4. На числовій лінії це показано із замкнутим колом при негативному 1 та відкритим колом на 4 із затіненням між замкнутими та відкритими колами. Його інтервальне позначення від'ємне від 1 до 4 в дужках і дужках.

    Приклад\(\PageIndex{3}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(3x−4<5\) і\(4x+9\geq 1\).

    Відповідь

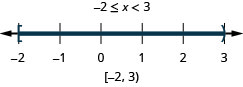
    Розв'язок від'ємний 2 менше або дорівнює x, який менше 3. На числовій лінії це показано із замкнутим колом при негативному 2 та відкритим колом на 3 із затіненням між замкнутими та відкритими колами. Його інтервальне позначення від'ємне від 2 до 3 в дужках і дужках.

    ВИРІШИТИ СКЛАДНУ НЕРІВНІСТЬ З «І».
    1. Вирішити кожну нерівність.
    2. Графік кожного рішення. Потім графуйте числа, які роблять обидві нерівності істинними.
      На цьому графіку показано розв'язання складної нерівності.
    3. Запишіть рішення в інтервальних позначеннях.
    Приклад\(\PageIndex{4}\)

    Вирішити\(3(2x+5)\leq 18\) і\(2(x−7)<−6\). Графік розв'язку і запишіть рішення в інтервальне позначення.

    Відповідь
      \(3(2x+5)\leq 18\) і \(2(x−7)<−6\)
    Вирішити кожну
    нерівність.    		 \(6x+15\leq 18\)   \(2x−14<−6\)
      \(6x\leq 3\)   \(2x<8\)
      \(x\leq \frac{1}{2}\) і \(x<4\)
    Графік кожного
    рішення.    		 .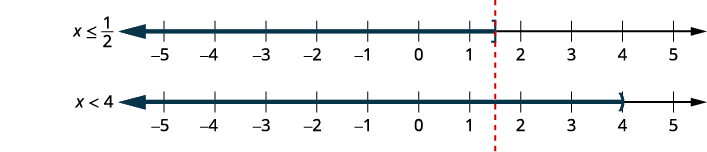
    Графік числа
    , які роблять обидві
    нерівності істинними.    		 .
    Запишіть рішення
    в інтервальних позначеннях.    		 \((−\infty, \frac{1}{2}]\)
    Приклад\(\PageIndex{5}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(2(3x+1)\leq 20\) і\(4(x−1)<2\).

    Відповідь

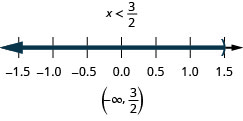
    Розчин х менше трьох половинок. На числовій лінії вона показана з відкритим колом на три половинки з затіненням зліва від нього. Його інтервальне позначення є негативною нескінченністю до трьох половинок в дужках.

    Приклад\(\PageIndex{6}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(5(3x−1)\leq 10\) і\(4(x+3)<8\).

    Відповідь

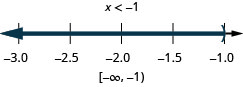
    Розв'язок x менше негативного 1. На числовій лінії він показаний з відкритим колом на 1 з затіненням зліва. Його інтервальне позначення є негативною нескінченністю до негативної 1 в дужках.

    Приклад\(\PageIndex{7}\)

    Вирішити\(\frac{1}{3}x−4\geq −2\) і\(−2(x−3)\geq 4\). Графік розв'язку і запишіть рішення в інтервальне позначення.

    Відповідь
      \(\frac{1}{3}x−4\geq −2\) і \(−2(x−3)\geq 4\)
    Вирішити кожну нерівність. \(\frac{1}{3}x−4\geq −2\)   \(−2x+6\geq 4\)
      \(\frac{1}{3}x\geq 2\)   \(−2x\geq −2\)
      \(x\geq 6\) і \(x\leq 1\)
    Графік кожного рішення. ...
    Графік числа, які
    роблять обидві нерівності
    істинними.    		 ...
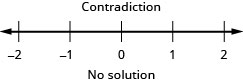
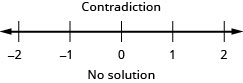
      Немає чисел, які роблять обидві нерівності правдивими.

    Це протиріччя, тому немає рішення. Немає чисел, які роблять обидві нерівності правдивими.

    Це протиріччя, тому немає рішення. Немає чисел, які роблять обидві нерівності правдивими.

    Це протиріччя, тому рішення немає.
    Приклад\(\PageIndex{8}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(\frac{1}{4}x−3\geq −1\) і\(−3(x−2)\geq 2\).

    Відповідь

    Нерівність - це протиріччя. Отже, рішення немає. В результаті немає графіка числового рядка або інтервального позначення.

    Приклад\(\PageIndex{9}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(\frac{1}{5}x−5\geq −3\) і\(−4(x−1)\geq −2\).

    Відповідь

    Нерівність - це протиріччя. Отже, рішення немає. В результаті немає графіка або числового рядка або інтервалу позначення.

    Іноді ми маємо складну нерівність, яку можна записати більш стисло. Наприклад,\(a<x\) і\(x<b\) може бути написано просто як\(a<x<b\) і тоді ми називаємо це подвійною нерівністю. Дві форми еквівалентні.

    ПОДВІЙНА НЕРІВ

    Подвійна нерівність - це складна нерівність, така як\(a<x<b\). Вона еквівалентна\(a<x\) і\(x<b\).

    \[\text{Other forms:} \quad \begin{array} {lllll} {a<x<b} &{\text{is equivalent to }} &{a<x} &{\text{and}} &{x<b} \\ {a\leq x\leq b} &{\text{is equivalent to }} &{a\leq x} &{\text{and}} &{x\leq b} \\ {a>x>b} &{\text{is equivalent to }} &{a>x} &{\text{and}} &{x>b} \\ {a\geq x\geq b} &{\text{is equivalent to }} &{a\geq x} &{\text{and}} &{x\geq b} \\ \end{array} \nonumber\]

    Для розв'язання подвійної нерівності виконуємо одну і ту ж операцію на всіх трьох «частинок» подвійної нерівності з метою виділення змінної в центрі.

    Приклад\(\PageIndex{10}\)

    Вирішити\(−4\leq 3x−7<8\). Графік розв'язку і запишіть рішення в інтервальне позначення.

    Відповідь
      \(-4 \leq 3x - 7 < 8\)
    Додайте 7 до всіх трьох частин. \( -4 \,{\color{red}{+\, 7}} \leq 3x - 7 \,{\color{red}{+ \,7}} < 8 \,{\color{red}{+ \,7}}\)
    Спростити. \( 3 \le 3x < 15 \)
    Кожну частину розділіть на три. \( \dfrac{3}{\color{red}{3}} \leq \dfrac{3x}{\color{red}{3}} < \dfrac{15}{\color{red}{3}} \)
    Спростити. \( 1 \leq x < 5 \)
    Графік рішення. .
    Запишіть рішення в інтервальних позначеннях. \( [1, 5) \)

    Коли написано як подвійна нерівність\(1\leq x<5\), легко побачити, що рішення - це числа, що потрапили від одного до п'яти, включаючи одне, але не п'ять. Потім ми можемо графікувати рішення відразу, як ми зробили вище.

    Інший спосіб графіка рішення\(1\leq x<5\) полягає в графіку як рішення, так\(x\geq 1\) і рішення\(x<5\). Потім ми знайдемо числа, які роблять обидві нерівності правдивими, як ми це робили в попередніх прикладах.

    Приклад\(\PageIndex{11}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(−5\leq 4x−1<7\).

    Відповідь

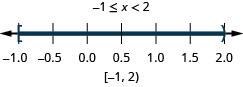
    Розв'язок негативний 1 менше або дорівнює x, який менше 2. Його графік має замкнуте коло при негативному 1 і відкрите коло на 2 із затіненням між замкнутими та відкритими колами. Його інтервальне позначення від'ємне від 1 до 2 в дужках і дужках.

    Приклад\(\PageIndex{12}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальних позначеннях:\(−3<2x−5\leq 1\).

    Відповідь

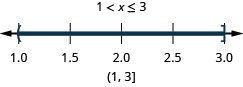
    Розчин 1 менше х, що менше або дорівнює 3. Його графік має відкрите коло на 1 і замкнуте коло на 3 з затіненням між замкнутими і відкритими колами. Його інтервальне позначення від'ємне від 1 до 3 в дужках і дужці.

    Вирішити складні нерівності за допомогою «або»

    Щоб вирішити складну нерівність за допомогою «або», ми починаємо так само, як і зі складеною нерівністю з «і» - ми вирішуємо дві нерівності. Тоді ми знаходимо всі числа, які роблять нерівність істинною.

    Подібно до того, як Сполучені Штати є об'єднанням всіх 50 штатів, рішенням буде об'єднання всіх чисел, які роблять нерівність істинною. Щоб знайти рішення складної нерівності, ми розглянемо графіки кожної нерівності, знаходимо числа, які належать до будь-якого графіка, і складемо всі ці числа разом.

    Щоб записати рішення в інтервальній нотації, ми часто будемо використовувати символ об'єднання\(\cup\), щоб показати об'єднання розв'язків, показаних на графіках.

    ВИРІШИТИ СКЛАДНУ НЕРІВНІСТЬ ЗА ДОПОМОГОЮ «АБО».
    1. Вирішити кожну нерівність.
    2. Графік кожного рішення. Потім графік числа, які роблять нерівність істинною.
    3. Запишіть рішення в інтервальних позначеннях.
    Приклад\(\PageIndex{13}\)

    Вирішити\(5−3x\leq −1\) або\(8+2x\leq 5\). Графік розв'язку і запишіть рішення в інтервальне позначення.

    Відповідь
      \(5−3x\leq −1\) або \(8+2x\leq 5\)
    Вирішити кожну нерівність. \(5−3x\leq −1\)   \(8+2x\leq 5\)
      \(−3x\leq −6\)   \(2x\leq −3\)
      \(x\geq 2\) або \(x\leq −\frac{3}{2}\)
    Графік кожного рішення. .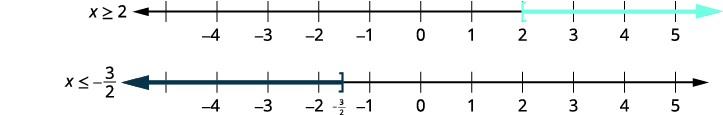
    Числа графіків, які
    роблять нерівність
    істинною.    		 .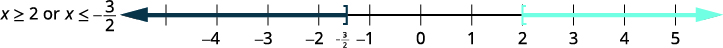
      \((−\infty,−32]\cup[2,\infty)\)
    Приклад\(\PageIndex{14}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальне позначення:\(1−2x\leq −3\) або\(7+3x\leq 4\).

    Відповідь

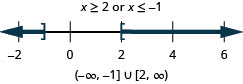
    Розчин х більше або дорівнює 2 або х менше або дорівнює 1. Графік розв'язків на числовій лінії має замкнуте коло при негативному 1 і затінення ліворуч і замкнуте коло на 2 з затіненням праворуч. Інтервальне позначення - це об'єднання негативної нескінченності до негативної 1 у дужках і дужці та 2 та нескінченності в дужці та дужках.

    Приклад\(\PageIndex{15}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальне позначення:\(2−5x\leq −3\) або\(5+2x\leq 3\).

    Відповідь

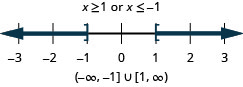
    Розв'язок х більше або дорівнює 1 або х менше або дорівнює від'ємному 1. Графік розв'язків на числовій лінії має замкнуте коло при від'ємному 1 і затінення ліворуч і замкнуте коло на 1 з затіненням праворуч. Інтервальне позначення - це об'єднання негативної нескінченності до негативної 1 у дужках і дужці та 1 та нескінченності в дужці та дужках.

    Приклад\(\PageIndex{16}\)

    Вирішити\(\frac{2}{3}x−4\leq 3\) або\(\frac{1}{4}(x+8)\geq −1\). Графік розв'язку і запишіть рішення в інтервальне позначення.

    Відповідь
      \(\frac{2}{3}x−4\leq 3\) або \(\frac{1}{4}(x+8)\geq −1\)
    Вирішити кожну
    нерівність.    		 \(3(\frac{2}{3}x−4)\leq 3(3)\)   \(4⋅\frac{1}{4}(x+8)\geq 4⋅(−1)\)
      \(2x−12\leq 9\)   \(x+8\geq −4\)
      \(2x\leq 21\)   \(x\geq −12\)
      \(x\leq \frac{21}{2}\)    
      \(x\leq \frac{21}{2}\) або \(x\geq −12\)
    Графік кожного
    рішення.    		 .
    Числа графіків
    , які роблять
    нерівність істинною.    		 .
      Рішення охоплює всі дійсні числа.
      \((−\infty ,\infty )\)
    Приклад\(\PageIndex{17}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальне позначення:\(\frac{3}{5}x−7\leq −1\) або\(\frac{1}{3}(x+6)\geq −2\).

    Відповідь

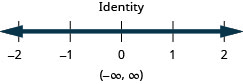
    Рішення - ідентичність. Його рішення на числовому рядку затінено для всіх значень. Розв'язок у інтервальній нотації - негативна нескінченність до нескінченності в дужках.

    Приклад\(\PageIndex{18}\)

    Вирішити складну нерівність. Графік розв'язку і запишіть рішення в інтервальне позначення:\(\frac{3}{4}x−3\leq 3\) або\(\frac{2}{5}(x+10)\geq 0\).

    Відповідь

    Рішення - ідентичність. Його рішення на числовому рядку затінено для всіх значень. Розв'язок у інтервальній нотації - негативна нескінченність до нескінченності в дужках.

    Розв'язуйте програми зі складними нерівностями

    Ситуації в реальному світі також передбачають складні нерівності. Ми будемо використовувати ту саму стратегію вирішення проблем, яку ми використовували для розв'язання програм лінійних рівнянь та нерівностей.

    Нагадаємо, стратегії вирішення проблем полягають в тому, щоб спочатку прочитати проблему і переконатися, що всі слова зрозумілі. Потім визначте те, що ми шукаємо, і призначте змінну для її представлення. Далі повторюємо задачу в одному реченні, щоб її було легко перевести в складну нерівність. Останнім, ми вирішимо складну нерівність.

    Приклад\(\PageIndex{19}\)

    Через посуху в Каліфорнії багато громад мають багаторівневі норми води. Існують різні тарифи для збереження використання, нормального використання та надмірного використання. Використання вимірюється кількістю сотень кубічних футів (hcf), якими користується власник майна.

    Протягом літа власник нерухомості буде платити $24.72 плюс $1.54 за hcf для нормального використання. Рахунок за нормальне використання буде між або дорівнює $57.06 і $171.02. Скільки hcf може використовувати власник, якщо він хоче, щоб його використання залишалося в нормальному діапазоні?

    Відповідь
    Визначте, що ми шукаємо. Кількість hcf він може використовувати і залишатися в діапазоні виставлення рахунків «нормальне використання».
    Назвіть те, що ми шукаємо. Нехай x = x = кількість hcf, який він може використовувати.
    Перевести на нерівність. Білл становить $24.72 плюс $1.54 рази кількість hcf, який він використовує для\(24.72+1.54x\).
     

    \(\color{Cerulean}{\underbrace{\color{black}{\text{His bill will be between or equal to }$57.06\text{ and }$171.02.}}}\)

    \(57.06 \leq 24.74 + 1.54x \leq 171.02 \)
    Вирішити нерівність.

    \(57.06 \leq 24.74 + 1.54x \leq 171.02\)

    \(57.06 \,{\color{red}{- \,24.72}}\leq 24.74 \,{\color{red}{- \,24.72}} + 1.54x \leq 171.02 \,{\color{red}{- \,24.72}}\)

    \( 32.34 \leq 1.54x \leq 146.3\)

    \( \dfrac{32.34}{\color{red}{1.54}} \leq \dfrac{1.54x}{\color{red}{1.54}} \leq \dfrac{146.3}{\color{red}{1.54}}\)

    \( 21 \leq x \leq 95 \)
    Дайте відповідь на питання. Власник нерухомості може використовувати\(21–95\) hcf і все ще потрапляти в діапазон виставлення рахунків «нормальне використання».
    Приклад\(\PageIndex{20}\)

    Через посуху в Каліфорнії багато громад зараз мають багаторівневі норми води. Існують різні тарифи для збереження використання, нормального використання та надмірного використання. Використання вимірюється кількістю сотень кубічних футів (hcf), якими користується власник майна.

    Протягом літа власник нерухомості буде платити $24.72 плюс $1.32 за hcf за збереження використання. Рахунок за використання збереження буде між або дорівнює $31.32 і $52.12. Скільки hcf може використовувати власник, якщо вона хоче, щоб її використання залишалося в діапазоні збереження?

    Відповідь

    Домовласник може використовувати\(5–20\) hcf і все ще потрапляти в діапазон виставлення рахунків «використання збереження».

    Приклад\(\PageIndex{21}\)

    Через посуху в Каліфорнії багато громад мають багаторівневі норми води. Існують різні тарифи для збереження використання, нормального використання та надмірного використання. Використання вимірюється кількістю сотень кубічних футів (hcf), якими користується власник майна.

    Протягом зими власник нерухомості буде платити $24.72 плюс $1.54 за hcf для нормального використання. Рахунок за нормальне використання буде між або дорівнює $49,36 і $86.32. Скільки hcf йому буде дозволено використовувати, якщо він хоче, щоб його використання залишалося в нормальному діапазоні?

    Відповідь

    Домовласник може використовувати\(16–40\) hcf і все ще потрапляти в діапазон виставлення рахунків «нормальне використання».

    Отримайте доступ до цього інтернет-ресурсу для додаткових інструкцій та практики з вирішенням складних нерівностей.

    • Складні нерівності

    Ключові концепції

    • Як вирішити складну нерівність за допомогою «і»
      1. Вирішити кожну нерівність.
      2. Графік кожного рішення. Потім графуйте числа, які роблять обидві нерівності істинними. На цьому графіку показано розв'язання складної нерівності.
      3. Запишіть рішення в інтервальних позначеннях.
    • Подвійна нерівність
      • Подвійна нерівність - це складна нерівність, така як\(a<x<b\). Це еквівалентно\(a<x\) і\(x<b.\)

        іншим формам:\ [\ begin {align*} a<x<b &\ text {еквівалентно} & a<x\;\ text {і}\; x<b\
        a≤x≤b &\ text {еквівалентно} & a≤x\;\ text {і}\; x≤b\ \
        a>x>b &\ text {еквівалентно} & & a>x\;\ текст {і}\; x>b\
        a≥x≥b &\ text {еквівалентно} & a≥x\;\ text {і}\; x≥b\ end {align*}\]
    • Як вирішити складну нерівність за допомогою «або»
      1. Вирішити кожну нерівність.
      2. Графік кожного рішення. Потім графік числа, які роблять нерівність істинною.
      3. Запишіть рішення в інтервальних позначеннях.

    Глосарій

    складна нерівність
    Складна нерівність складається з двох нерівностей, пов'язаних словом «і» або словом «або».