2.6: Вирішити лінійні нерівності
- Page ID
- 59784
До кінця цього розділу ви зможете:
- Нерівності графа на числовому рядку
- Вирішити лінійні нерівності
- Переведіть слова на нерівність і вирішуйте
- Розв'язуйте програми з лінійними нерівностями
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Перекласти з алгебри на англійську:\(15>x\).
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Перевести на алгебраїчний вираз:\(15\) менше, ніж\(x\).
Якщо ви пропустили цю проблему, перегляньте [посилання].
Нерівності графа на числовій лінії
Яке число зробить нерівність\(x>3\) правдою? Ви думаєте, «\(x\)може бути чотири»? Це правильно, але\(x\) може бути 6, теж, або 37, або навіть 3.001. Будь-яке число більше трьох є розв'язком нерівності\(x>3\). Ми показуємо всі розв'язки нерівності\(x>3\) на числовій лінії шляхом затінення у всіх числах праворуч від трьох, щоб показати, що всі числа більше трьох є розв'язками. Оскільки цифра три сама по собі не є рішенням, ми ставимо відкриту дужку на три.
Ми також можемо представляти нерівності за допомогою інтервальних позначень. Немає верхнього кінця вирішення цієї нерівності. У інтервальних позначеннях виражаємо\(x>3\) як\((3,\infty)\). Символ\(\infty\) читається як «нескінченність». Це не фактичне число. \(\PageIndex{1}\)На малюнку показані як числовий рядок, так і інтервальні позначення.
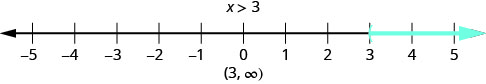
Ми використовуємо символ лівої дужки, (, щоб показати, що кінцева точка нерівності не включена. Символ лівої дужки, [, показує, що кінцева точка включена.
Нерівність\(x\leq 1\) означає всі числа менше або рівні одиниці. Тут нам потрібно показати, що одне - це теж рішення. Ми робимо це, поставивши кронштейн на\(x=1\). Потім ми затінюємо у всіх числах зліва від одного, щоб показати, що всі числа менше одиниці є розв'язками (рис.\(\PageIndex{2}\)). Немає нижнього кінця цих чисел. Запишемо\(x\leq 1x\leq 1 \) в інтервалі позначення як\((−\infty,1]\). Символ\(−\infty\) читається як «негативна нескінченність».
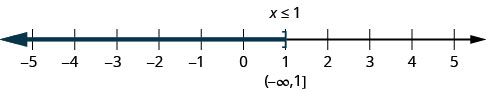
\(\PageIndex{3}\)На малюнку показані як числові рядки, так і інтервальні позначення.

Позначення для нерівностей на числовому рядку і в інтервальній нотації використовують однакові символи для вираження кінцевих точок інтервалів.
Графік кожної нерівності на числовому рядку і запишіть в інтервальні позначення.
- \(x\geq −3\)
- \(x<2.5\)
- \(x\leq −\frac{3}{5}\)
- Відповідь
-
ⓐ
\( x \geq -3 \) Затіньте праворуч від\(−3\), і поставте дужку на\(−3\). 
Запишіть в інтервальних позначеннях. \( [-3, \infty) \) ⓑ
\( x < 2.5 \) Заштрихуйте зліва 2,5 і поставте дужку в 2,5. 
Запишіть в інтервальних позначеннях. \( (-\infty, 2.5) \) ⓒ
\( x \leq -\dfrac{3}{5} \) Затіньте зліва від\(−\frac{3}{5}\), і поставте дужку на\(−\frac{3}{5}\). 
Запишіть в інтервальних позначеннях. \( \bigg( -\infty, \dfrac{3}{5}\bigg] \)
Графік кожної нерівності на числовому рядку і запишіть в інтервальні позначення:
- \(x>2\)
- \(x\leq −1.5\)
- \(x\geq \frac{3}{4}\).
- Відповідь
-
ⓐ
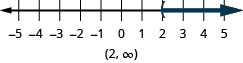
ⓑ
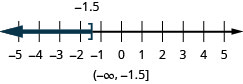
ⓒ
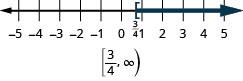
Графік кожної нерівності на числовому рядку і запишіть в інтервальні позначення:
- \(x\leq −4\)
- \(x\geq 0.5\)
- \(x<−\frac{2}{3}\).
- Відповідь
-
ⓐ
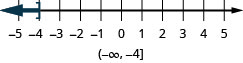
ⓑ

ⓒ
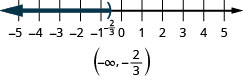
Які числа більше двох, але менше п'яти? Ви думаєте сказати,\(2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99\)? Ми можемо уявити всі числа від двох до п'яти з нерівністю\(2<x<5\). Ми можемо показати\(2<x<5\) на числовому рядку, затінюючи всі числа між двома і п'ятьма. Знову ж таки, ми використовуємо дужки, щоб показати цифри два і п'ять не включені. Див. Малюнок.

Графік кожної нерівності на числовому рядку і запишіть в інтервальні позначення.
ⓐ\(−3<x<4\) ⓑ\(−6\leq x<−1\) ⓒ\(0\leq x\leq 2.5\)
- Відповідь
-
ⓐ
\(-3 < x < 4\) Тінь між\(−3\) і 4.
Поставте дужки на\(−3\) і 4.
Запишіть в інтервальних позначеннях. \( (-3,4) \) ⓑ
\( -6 \leq x < -1 \) Затінення між\(−6\) і −1.
Поставте дужку за адресою\(−6\),
а дужку — −1.
Запишіть в інтервальних позначеннях. \( [-6,1) \) ⓒ
\( 0 \leq x \leq 2.5 \) Тінь між 0 і 2,5.
Поставте кронштейн на 0 і на 2,5.
Запишіть в інтервальних позначеннях. \( [0, 2.5] \)
Графік кожної нерівності на числовому рядку і запишіть в інтервальні позначення:
ⓐ\(−2<x<1\) ⓑ\(−5\leq x<−4\) ⓒ\(1\leq x\leq 4.25\)
- Відповідь
-
ⓐ
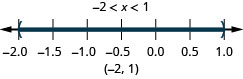
ⓑ
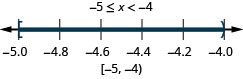
ⓒ
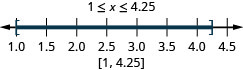
Графік кожної нерівності на числовому рядку і запишіть в інтервальні позначення:
ⓐ\(−6<x<2\) ⓑ\(−3\leq x< −1\) ⓒ\(2.5\leq x\leq 6\)
- Відповідь
-
ⓐ
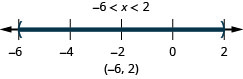
ⓑ
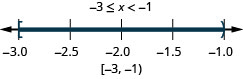
ⓒ
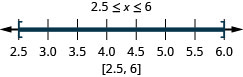
Вирішити лінійні нерівності
Лінійна нерівність дуже схожа на лінійне рівняння, але знак рівності замінюється знаком нерівності. Лінійна нерівність - це нерівність в одній змінній, яка може бути записана в одній з форм\(ax+b<c\)\(ax+b\leq c\),,\(ax+b>c\), або\(ax+b\geq c\).
Лінійна нерівність - це нерівність в одній змінній, яка може бути записана в одній з наступних форм де\(a, \, b,\) і\(c\) є дійсними числами і\(a≠0\):
\[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]
Коли ми вирішували лінійні рівняння, ми змогли використовувати властивості рівності для додавання, віднімання, множення або ділення обох сторін і все ще зберегти рівність. Подібні властивості дотримуються і для нерівностей.
Ми можемо додати або відняти однакову величину з обох сторін нерівності і все одно зберегти нерівність. Наприклад:
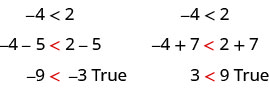
Зверніть увагу, що знак нерівності залишився колишнім.
Це призводить нас до додавання і віднімання властивостей нерівності.
Для будь-яких чисел\(a, \, b,\) і\(c,\) якщо\(a<b\), то
\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]
Ми можемо додати або відняти однакову величину з обох сторін нерівності і все одно зберегти нерівність
Що відбувається з нерівністю, коли ми ділимо або множимо обидві сторони на константу?
Давайте спочатку помножимо і розділимо обидві сторони на позитивне число.
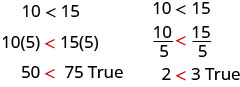
Ознаки нерівності залишилися колишніми.
Чи залишається нерівність однаковою, коли ми ділимо або множимо на від'ємне число?
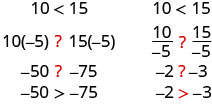
Зверніть увагу, що коли ми заповнили знаки нерівності, ознаки нерівності змінили свій напрямок.
Коли ми ділимо або множимо нерівність на додатне число, знак нерівності залишається тим самим. Коли ми ділимо або множимо нерівність на негативне число, знак нерівності змінюється.
Це дає нам властивість множення та поділу нерівності.
Для будь-яких номерів\(a, \, b,\) і\(c,\)
\[\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}\]
Коли ми ділимо або множимо нерівність на\(a\):
- додатне число, нерівність залишається незмінною.
- негативне число, нерівність змінюється.
Іноді при вирішенні нерівності, як в наступному прикладі, змінна закінчується справа. Ми можемо переписати нерівність у зворотному напрямку, щоб отримати змінну ліворуч.
\[x>a \text{ has the same meaning as } a<x \nonumber \]
Подумайте про це як «Якщо Ксандер вищий за Енді, то Енді коротший, ніж Ксандер».
Вирішити кожну нерівність. Графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
ⓐ\(x−\frac{3}{8}\leq \frac{3}{4}\) ⓑ\(9y<54\) ⓒ\(−15<\frac{3}{5}z\)
- Відповідь
-
ⓐ
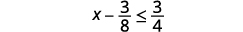
Додайте 3838 до обох сторін нерівності. 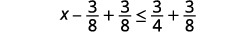
Спростити. 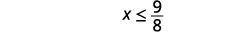
Графік розв'язку на числовому рядку. 
Запишіть рішення в інтервальних позначеннях. 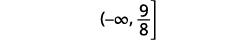
ⓑ
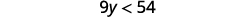
Розділіть обидві сторони нерівності на 9; оскільки
9 позитивна, нерівність залишається однаковою.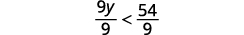
Спростити. 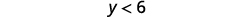
Графік розв'язку на числовому рядку. 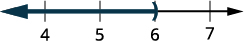
Запишіть рішення в інтервальних позначеннях. 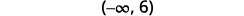
ⓒ
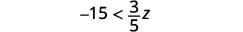
Помножте обидві сторони нерівності на\(\frac{5}{3}\).
Оскільки\(\frac{5}{3}\) є позитивним, нерівність залишається незмінною.
Спростити. 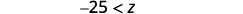
Перепишіть зі змінною зліва. 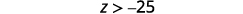
Графік розв'язку на числовому рядку. 
Запишіть рішення в інтервальних позначеннях. 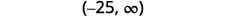
Розв'яжіть кожну нерівність, графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях:
ⓐ\(p−\frac{3}{4}\geq \frac{1}{6}\) ⓑ\(9c>72\) ⓒ\(24\leq \frac{3}{8}m\)
- Відповідь
-
ⓐ
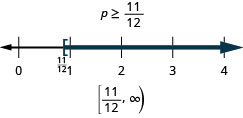
ⓑ
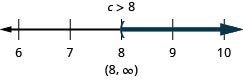
ⓒ
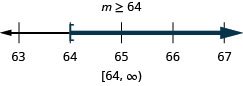
Розв'яжіть кожну нерівність, графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях:
ⓐ\(r−\frac{1}{3}\leq \frac{7}{12}\) ⓑ\(12d\leq 60\) ⓒ\(−24<\frac{4}{3}n\)
- Відповідь
-
ⓐ
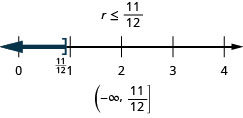
ⓑ
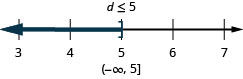
ⓒ
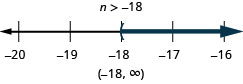
Будьте обережні, коли ви множите або ділите на від'ємне число - пам'ятайте, щоб змінити знак нерівності.
Розв'яжіть кожну нерівність, графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
ⓐ\(−\frac{1}{3}m\geq \frac{6}{5}\) ⓑ\(\frac{n}{−2} \geq 8\)
- Відповідь
-
ⓐ
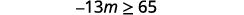
Розділіть обидві сторони нерівності на\(−\frac{1}{3}\).
Оскільки\(−\frac{1}{3}\) є негативом, нерівність змінюється.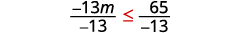
Спростити. 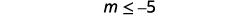
Графік розв'язку на числовому рядку. 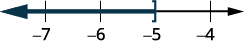
Запишіть рішення в інтервальних позначеннях. 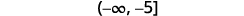
ⓑ
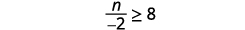
Помножте обидві сторони нерівності на\(−2\).
Оскільки\(−2\) є негативом, нерівність змінюється.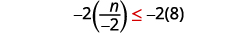
Спростити. 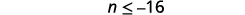
Графік розв'язку на числовому рядку. 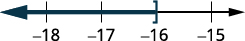
Запишіть рішення в інтервальних позначеннях. 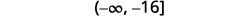
Розв'яжіть кожну нерівність, графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях:
ⓐ\(−8q<32\) ⓑ\(\frac{k}{−12} \leq 15\).
- Відповідь
-
ⓐ
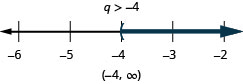
ⓑ
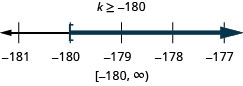
Розв'яжіть кожну нерівність, графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях:
ⓐ\(−7r\leq −70\) ⓑ\(\frac{u}{−4}\geq −16\).
- Відповідь
-
ⓐ
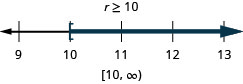
ⓑ
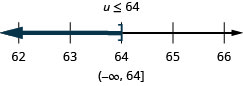
Більшість нерівностей займе не один крок для вирішення. Ми слідуємо тим самим крокам, які ми використовували в загальній стратегії вирішення лінійних рівнянь, але обов'язково звертайте пильну увагу, коли ми множимо або ділимо, щоб ізолювати змінну.
Розв'яжіть нерівність\(6y\leq 11y+17\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
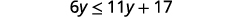
Відніміть 11y11y з обох сторін
, щоб зібрати змінні зліва.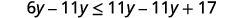
Спростити. 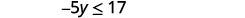
Розділіть обидві сторони нерівності на −5, −5
та оберніть нерівність.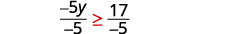
Спростити. 
Графік розв'язку на числовому рядку. 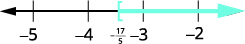
Запишіть рішення в інтервальних позначеннях. 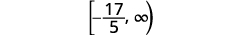
Розв'яжіть нерівність, графуйте рішення на числовому рядку і запишіть рішення в інтервальній нотації:\(3q\geq 7q−23\).
- Відповідь
-
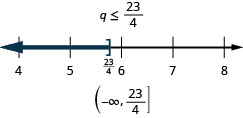
Розв'яжіть нерівність, графуйте рішення на числовому рядку і запишіть рішення в інтервальній нотації:\(6x<10x+19\).
- Відповідь
-
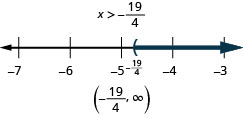
При вирішенні нерівностей зазвичай найпростіше зібрати змінні на тій стороні, де коефіцієнт змінної найбільший. Це усуває негативні коефіцієнти, і тому нам не доведеться множити або ділити на негатив - це означає, що нам не потрібно пам'ятати, щоб змінити знак нерівності.
Розв'яжіть нерівність\(8p+3(p−12)>7p−28\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
\(8p+3(p−12)>7p−28\) Максимально спрощуйте кожну сторону. Розподілити. \(8p+3p−36>7p−28\) Поєднуйте подібні терміни. \(11p−36>7p−28\) Відніміть\(7p\) з обох сторін, щоб зібрати
змінні зліва, так як\(11>7\).\(11p−36−7p>7p−28−7p\) Спростити. \(4p−36>−28\) Додайте\(36\) в обидві сторони, щоб зібрати
константи праворуч.\(4p−36+36>−28+36\) Спростити. \(4p>8\) Розділіть обидві сторони нерівності на
\(4\); нерівність залишається однаковою.\(\dfrac{4p}{4}>\dfrac{8}{4}\) Спростити. \(p>2\) Графік розв'язку на числовому рядку. 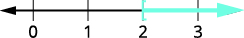
Запишіть рішення в інтервальних позначеннях. \((2,\infty)\)
Розв'яжіть нерівність\(9y+2(y+6)>5y−24\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
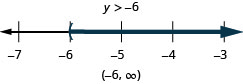
Розв'яжіть нерівність\(6u+8(u−1)>10u+32\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
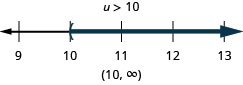
Подібно до того, як деякі рівняння є ідентичностями, а деякі - протиріччями, нерівності можуть бути ідентичностями або протиріччями. Ми визнаємо ці форми, коли нам залишається тільки константи, коли ми вирішуємо нерівність. Якщо результат є істинним твердженням, у нас є ідентичність. Якщо в результаті виявиться помилкове твердження, у нас виникає протиріччя.
Розв'яжіть нерівність\(8x−2(5−x)<4(x+9)+6x\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
Максимально спрощуйте кожну сторону. \(8x−2(5−x)<4(x+9)+6x\) Розподілити. \(8x−10+2x<4x+36+6x\) Поєднуйте подібні терміни. \(10x−10<10x+36\) Відніміть\({\color{red}{10x}}\) з обох сторін, щоб зібрати змінні зліва. \(10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}\) Спростити. \(−10<36\) Вони пішли, і у нас є правдиве
твердження.\(x\)Нерівність - це ідентичність.
Рішенням є всі дійсні числа.Графік розв'язку на числовому рядку. 
Запишіть рішення в інтервальних позначеннях. \((−\infty,\infty)\)
Розв'яжіть нерівність\(4b−3(3−b)>5(b−6)+2b\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
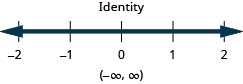
Розв'яжіть нерівність\(9h−7(2−h)<8(h+11)+8h\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
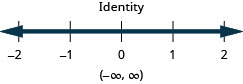
Ми можемо очистити дроби в нерівностях так само, як ми це робили в рівняннях. Знову ж таки, будьте обережні зі знаками при множенні або діленні на негатив.
Розв'яжіть нерівність\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\) Помножте обидві сторони на РК-дисплей, 24,
щоб очистити фракції.\({\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\) Спростити. \( 8a - 3a > 5a + 18 \) Поєднуйте подібні терміни. \( 5a > 5a + 18\) Відніміть\(5a\) з обох сторін, щоб зібрати
змінні зліва.\( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\) Спростити. \(0 > 18 \) Заява неправдиве. Нерівність - це протиріччя.
Рішення немає.Графік розв'язку на числовому рядку. 
Запишіть рішення в інтервальних позначеннях. Рішення немає.
Розв'яжіть нерівність\(\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
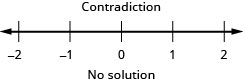
Розв'яжіть нерівність\(\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}\), графік розв'язку на числовому рядку і запишіть рішення в інтервальних позначеннях.
- Відповідь
-
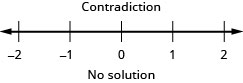
Перекласти на нерівність і вирішити
Щоб перевести англійські речення в нерівності, нам потрібно розпізнати фрази, які вказують на нерівність. Деякі слова прості, на кшталт «більше ніж» і «менше, ніж». Але інші не такі очевидні. У таблиці наведені деякі поширені фрази, які вказують на нерівності.
| \(>\) | \(\geq\) | \(<\) | \(\leq\) |
|---|---|---|---|
| \ (>\) ">\)» data-valign="middle» class="lt-math-17389">більше, ніж більше, ніж перевищує |
\ (\ geq\)» data-valign="midle">більше або дорівнює принаймні не менше мінімального |
\ менше, <\)» data-valign="middle"> ніж менше, ніж має менше, ніж менше, ніж нижче |
\ (\ leq\)» data-valign="middle">менше або дорівнює не більше не більше максимуму |
Перекладіть і вирішуйте. Потім графік рішення на числовому рядку і запишіть рішення в інтервальних позначеннях.
\[\text{Twenty-seven less than }x\text{ is at least }48.\nonumber\]
- Відповідь
-

Перекласти. \(x - 27 \geq 48\) Вирішити - додайте 27 до обох сторін. \( x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}\) Спростити. \(x \geq 75\) Графік на числовому рядку. 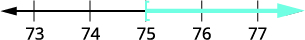
Запишіть в інтервальних позначеннях. \([75, \infty)\)
Перекладіть і вирішуйте. Потім графік рішення на числовому рядку і запишіть рішення в інтервальних позначеннях.
\[\text{Nineteen less than } p \text{ is no less than }47.\nonumber\]
- Відповідь
-
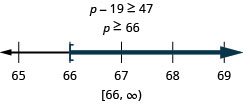
Перекладіть і вирішуйте. Потім графік рішення на числовому рядку і запишіть рішення в інтервальних позначеннях.
\[\text{Four more than }a\text{ is at most }15.\nonumber\]
- Відповідь
-
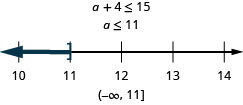
Розв'язуйте програми з лінійними нерівностями
Багато реальних життєвих ситуацій вимагають від нас вирішення нерівностей. Метод, який ми будемо використовувати для вирішення додатків з лінійними нерівностями, дуже схожий на той, який ми використовували, коли ми вирішували додатки з рівняннями.
Ми прочитаємо проблему і переконаємося, що всі слова зрозумілі. Далі ми визначимо, що ми шукаємо, і присвоїмо змінну для її представлення. Ми повторюємо проблему в одному реченні, щоб її було легко перевести в нерівність. Тоді ми вирішимо нерівність.
Іноді додаток вимагає, щоб рішення було цілим числом, але алгебраїчне рішення нерівності не є цілим числом. У такому випадку ми повинні округлити алгебраїчний розв'язок до цілого числа. Контекст програми визначатиме, округляємо ми вгору чи вниз.
Dawn виграла міні-грант у розмірі 4000 доларів на придбання планшетних комп'ютерів для свого класу. Планшети, які вона хотіла б придбати, коштують $254,12 кожен, включаючи податок та доставку. Яку максимальну кількість планшетів Dawn можна купити?
- Відповідь
-
\(\begin{array} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Choose a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{information to find it.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$4,000.} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15} \\{\text{But }n\text{ must be a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{Rounding down the price to } $250, 15} &{} \\ {\space\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\space\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Answer }\text{the question with a complete sentence.}} &{\text{Dawn can buy a maximum of 15 tablets.}} \\ \end{array}\)
Енджі має 20 доларів, щоб витратити на коробки для соку для дошкільного пікніка її сина. Кожна упаковка коробок для соку коштує $2,63. Яку максимальну кількість пачок вона може купити?
- Відповідь
-
У Енджі можна купити 7 упаковок соку.
Даніель хоче здивувати свою дівчину з днем народження в її улюбленому ресторані. Це буде коштувати $42.75 на людину за вечерю, включаючи чайові та податок. Його бюджет на вечірку становить 500 доларів. Яку максимальну кількість людей може мати Данило на вечірці?
- Відповідь
-
Даніель може мати 11 осіб на вечірці.
Телефонний план Талейші коштує їй $28,80 на місяць плюс $0.20 за текстове повідомлення. Скільки текстових повідомлень вона може відправляти/отримувати і тримати її щомісячний телефонний рахунок не більше $50?
- Відповідь
-
\(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can make}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to represent that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step 4. Translate }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.80+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 0.2t\leq 21.2} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\space\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text messages to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}\)
Серхіо та Лізет мають дуже жорсткий бюджет на відпустку. Вони планують орендувати автомобіль у компанії, яка стягує $75 на тиждень плюс $0.25 за милю. Скільки миль вони можуть проїхати протягом тижня і все ще тримати в межах свого бюджету $200?
- Відповідь
-
Серхіо і Лізет можуть проїхати не більше 500 миль.
Раміна рахунок за опалення становить $5.42 на місяць плюс $1,08 за терм. Скільки терм може використовувати Рамін, якщо він хоче, щоб його рахунок за опалення становив максимум $87.50.
- Відповідь
-
Раміна рахунок за опалення становить $5.42 на місяць плюс $1,08 за терм. Скільки терм може використовувати Рамін, якщо він хоче, щоб його рахунок за опалення становив максимум $87.50.
Прибуток - це гроші, які залишаються при відніманні витрат з виручки. У наступному прикладі ми знайдемо кількість робочих місць, які малий бізнес-леді повинен робити щомісяця, щоб отримати певну суму прибутку.
Фелісіті має каліграфічний бізнес. Вона стягує $2,50 за запрошення на весілля. Її щомісячні витрати складають 650 доларів. Скільки запрошень вона повинна написати, щоб заробити прибуток не менше 2800 доларів на місяць?
- Відповідь
-
\(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\space\space\space\text{Choose a variable to represent it.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$2.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\space\space\space 2.50j−650\geq 2,800} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 2.5j\geq 3,450} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space j\geq 1,380 \text{ invitations}} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\space\space\space \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\space\space\space $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Felicity must write at least }1,380\text{ invitations.}} \\ \end{array}\)
Калеб має домашню тварину сидячи бізнес. Він стягує 32 долари на годину. Його щомісячні витрати складають 2 272 долари. Скільки годин він повинен пропрацювати, щоб отримувати прибуток не менше 800 доларів на місяць?
- Відповідь
-
Калеб повинен працювати не менше 96 годин.
Елліот має бізнес з обслуговування ландшафту. Його щомісячні витрати складають 1100 доларів. Якщо він стягує 60 доларів за роботу, скільки робочих місць він повинен зробити, щоб отримувати прибуток щонайменше 4000 доларів на місяць?
- Відповідь
-
Елліот повинен працювати не менше 85 робочих місць.
Існує безліч ситуацій, в яких кілька величин сприяють загальному витраті. Ми повинні обов'язково враховувати всі індивідуальні витрати, коли ми вирішуємо подібні проблеми.
Малік планує шестиденну літню відпустку. У нього 840 доларів заощаджень, і він заробляє 45 доларів на годину на репетиторство. Поїздка обійдеться йому в 525 доларів за авіаквитки, 780 доларів за їжу та визначні пам'ятки та 95 доларів за ніч за готель. Скільки годин повинен репетитор, щоб вистачило грошей на оплату поїздки?
- Відповідь
-
\(\begin{array} {ll} {} &{} \\ {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\space \text{Choose a variable to represent that}} &{} \\ {\space\space\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The cost of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must be less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space \text{Translate into an inequality.}} &{525+780+95(6)\leq 840+45h} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,875\leq 840+45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,035\leq 45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 23\leq h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45h} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45(23)} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at least }23\text{ hours.}} \\ \end{array}\)
Найкращий друг Бренда має весілля призначення, і подія триватиме три дні. Бренда має 500 доларів заощаджень і може заробляти 15 доларів на годину няні. Вона розраховує заплатити 350 доларів авіаквитків, 375 доларів за їжу та розваги та 60 доларів за ніч за свою частку в готельному номері. Скільки годин вона повинна сидіти, щоб мати достатньо грошей, щоб оплатити поїздку?
- Відповідь
-
Бренда повинна няньчити не менше 27 годин.
Josue хоче відправитися в 10-нічну дорожню подорож з друзями наступної весни. Це обійдеться йому в 180 доларів за газ, 450 доларів за їжу та 49 доларів за ніч, щоб розділити номер у мотелі. Він має $520 заощаджень і може заробити $30 за під'їзну дорогу лопати сніг. Скільки під'їзних шляхів він повинен лопати, щоб мати достатньо грошей, щоб оплатити поїздку?
- Відповідь
-
Josue повинен лопати не менше 20 під'їзних шляхів.
Ключові концепції
- Нерівності, числові рядки та інтервальні позначення
\(x>a \quad x\geq a\quad x<a\quad x\leq a\)

- Лінійна нерівність
- Лінійна нерівність - це нерівність в одній змінній, яка може бути записана в одній з наступних форм, де a, b і c - дійсні числа і\(a\neq 0\):
\[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]
- Лінійна нерівність - це нерівність в одній змінній, яка може бути записана в одній з наступних форм, де a, b і c - дійсні числа і\(a\neq 0\):
- Властивість додавання та віднімання нерівності
- Для будь-яких чисел a, b і c, якщо a<b, то a<b, то
\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]
- Ми можемо додати або відняти однакову величину з обох сторін нерівності і все одно зберегти нерівність.
- Для будь-яких чисел a, b і c, якщо a<b, то a<b, то
- Властивість множення та ділення нерівності
- Для будь-яких чисел a, b і c,
\(\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}\)
- Для будь-яких чисел a, b і c,
- Фрази, що вказують на нерівності
\(>\) \(\geq\) \(<\) \(\leq\) \ (>\) ">більше ніж
більше, ніж
більше, ніж
перевищує\ (\ geq\)» data-valign="midle">більше або
дорівнює принаймні не менше
мінімального\ менше, <\)» data-valign="middle"> ніж менше, ніж має
менше, ніж
менше, ніж
нижче\ (\ leq\)» data-valign="middle">менше або
дорівнює не більше не більше
максимуму
