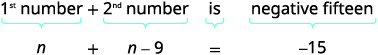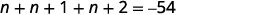2.3: Використовуйте стратегію вирішення проблем
- Page ID
- 59789
До кінця цього розділу ви зможете:
- Використовуйте стратегію вирішення проблем для проблем зі словами
- Вирішити проблеми з числовими словами
- Вирішити відсотки додатків
- Вирішуйте прості програми за інтересами
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Переведіть «шість менше двох разів\(x\)» в алгебраїчний вираз.
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Перетворіть 4.5% до десяткового.
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Перетворіть 0,6 до відсотка.
Якщо ви пропустили цю проблему, перегляньте [посилання].
Чи були у вас коли-небудь негативні переживання в минулому зі словами проблеми? Коли ми відчуваємо, що не маємо контролю, і продовжуємо повторювати негативні думки, ми створюємо бар'єри на шляху до успіху. Зрозумійте, що ваш негативний досвід із проблемами слів у вашому минулому. Щоб рухатися вперед, потрібно заспокоїти свої страхи і змінити свої негативні почуття.
Почніть зі свіжого аркуша і починайте думати про позитивні думки. Повторення деяких з наступних тверджень може бути корисним, щоб перетворити ваші думки позитивними. Мислення позитивних думок - це перший крок до успіху.
- Я думаю, що можу! Я думаю, що можу!
- Хоча проблеми зі словами були важкими в минулому, я думаю, я можу спробувати їх зараз.
- Я зараз краще підготовлена—думаю, я почну розбиратися в проблемах слів.
- Я можу вирішувати рівняння, тому що я практикував багато проблем і отримав допомогу, коли мені це було потрібно - я можу спробувати це з проблемами слів.
- Це може зайняти час, але я можу почати вирішувати проблеми зі словами.
- Ви зараз добре підготовлені і готові до успіху. Якщо ви візьмете під контроль і вірите, що можете бути успішними, ви зможете освоїти проблеми зі словами.
Використовуйте стратегію вирішення проблем для проблем Word
Тепер, коли ми можемо вирішувати рівняння, ми готові застосувати наші нові навички до проблем зі словами. Ми розробимо стратегію, яку зможемо використати для успішного вирішення будь-якої проблеми слова.
Звичайний щорічний снігопад на місцевому гірськолижному курорті становить 12 дюймів більше, ніж удвічі більше суми, яку він отримав в минулому сезоні. Звичайний щорічний снігопад становить 62 дюйми. Який був снігопад минулого сезону на гірськолижному курорті?
Рішення:
| Крок 1. Прочитайте проблему. | |
| Крок 2. Визначте, що ви шукаєте. | Яким був снігопад минулого сезону? |
| Крок 3. Назвіть те, що ми шукаємо, і виберіть змінну для його представлення. | Нехай\(s=\) снігопад в минулому сезоні. |
| Крок 4. Перекласти. Повторюйте проблему в одному реченні з усією важливою інформацією. |  |
| Перевести в рівняння. |  |
| Крок 5. Розв'яжіть рівняння. | 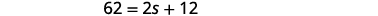 |
| Відніміть по 12 з кожного боку. | 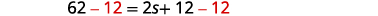 |
| Спростити. |  |
| Розділіть кожну сторону на дві. |  |
| Спростити. |  |
| Крок 6. Перевірте: По-перше, чи розумна наша відповідь? Так, маючи 25 дюймів снігу, здається, нормально. Проблема говорить, що нормальний снігопад на дванадцять дюймів більше, ніж удвічі більше, ніж в минулому сезоні. Двічі 25 - 50 і 12 більше, ніж 62. | |
| Крок 7. Дайте відповідь на питання. | Снігопад в минулому сезоні становив 25 дюймів. |
Гільєрмо купив підручники і зошити в книгарні. Кількість підручників становила в три більше, ніж удвічі більше зошитів. Він купив сім підручників. Скільки блокнотів він купив?
- Відповідь
-
Він купив два зошити
На цьому тижні Джеррі працював з головоломками судоку та кросвордами. Кількість загадок судоку, які він виконав, становить вісім більше, ніж в два рази перевищує кількість кросвордів. Він виконав 22 головоломки судоку. Скільки кросвордів він зробив?
- Відповідь
-
Він зробив сім кросвордів
Підсумовуємо ефективну стратегію вирішення проблем.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте, що ви шукаєте.
- Назвіть те, що ви шукаєте. Виберіть змінну для представлення цієї кількості.
- Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в рівняння алгебри.
- Розв'яжіть рівняння, використовуючи правильні методи алгебри.
- Перевірте відповідь у проблемі, щоб переконатися, що це має сенс.
- Відповісти на питання повним реченням.
Вирішити проблеми з числовим словом
Тепер ми будемо застосовувати стратегію вирішення проблем до «проблем з числом слів». Числові слова задачі дають деякі підказки про одне або кілька чисел, і ми використовуємо ці ключі для написання рівняння. Проблеми з числовими словами забезпечують хорошу практику використання Стратегії вирішення проблем.
Сума сім разів число і вісім дорівнює тридцяти шести. Знайдіть номер.
Рішення:
| Крок 1. Прочитайте проблему. | |
|---|---|
| Крок 2. Визначте, що ви шукаєте. | число |
|
Крок 3. Назвіть те, що ви шукаєте і вибрати змінну для її представлення. |
Нехай\(n=\) число. |
|
Крок 4. Перекласти: Повторюйте проблему як одне речення. Перевести в рівняння. |
|
|
Крок 5. Розв'яжіть рівняння. Відніміть вісім з кожного боку і спростіть. Розділіть кожну сторону на сім і спростіть. |
|
|
Крок 6. Перевірте. Чи сума сім разів чотири плюс вісім дорівнює 36? \[\begin{align*} 7·4+8 & \stackrel{?}{=}36 \\ 28+8 & \stackrel{?}{=}36 \\ 36 & =36✓ \end{align*}\] |
|
| Крок 7. Дайте відповідь на питання. | Число - 4. |
Ви помітили, що ми залишили деякі кроки, коли ми вирішили це рівняння? Якщо ви ще не готові залишити ці кроки, запишіть стільки, скільки вам потрібно.
Сума чотириразового числа і двох дорівнює чотирнадцяти. Знайдіть номер.
- Відповідь
-
\(3\)
Сума триразового числа і семи дорівнює двадцяти п'яти. Знайдіть номер.
- Відповідь
-
\(6\)
Деякі проблеми з числовими словами просять нас знайти два або більше чисел. Можливо, буде спокусливо назвати їх усі різними змінними, але поки що ми розв'язували рівняння лише з однією змінною. Щоб уникнути використання більше однієї змінної, ми визначимо числа через одну і ту ж змінну. Обов'язково уважно прочитайте проблему, щоб дізнатися, як всі цифри співвідносяться один з одним.
Сума двох чисел від'ємна п'ятнадцять. Одне число на дев'ять менше іншого. Знайдіть цифри.
Рішення:
| Крок 1. Прочитайте проблему. | |
| Крок 2. Визначте, що ви шукаєте. | два числа |
| Крок 3. Назвіть те, що ви шукаєте, вибравши змінну для представлення першого числа. «Одне число на дев'ять менше іншого». | Нехай\(n=1^{\text{st}}\) номер. \(n−9=2^{\text{nd}}\)число |
| Крок 4. Перекласти. Напишіть як одне речення. Перевести в рівняння. | Сума двох чисел від'ємна п'ятнадцять.
|
|
Крок 5. Розв'яжіть рівняння. Поєднуйте подібні терміни. Додайте дев'ять в кожну сторону і спростіть. Спростити. |
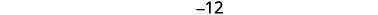 |
| Крок 6. Перевірте. Це\(−12\) дев'ять менше, ніж\(−3\)? \[\begin{align*}−3−9 & \stackrel{?}{=}−12 \\ −12 & =−12✓ \end{align*}\]Чи є їх сума\(−15?\)\[\begin{align*} −3+(−12) & \stackrel{?}{=}−15 \\ −15 & =−15✓ \end{align*}\] | |
| Крок 7. Дайте відповідь на питання. | Цифри -\(−3\) і\(−12\). |
Сума двох чисел від'ємна двадцять три. Одне число на сім менше іншого. Знайдіть цифри.
- Відповідь
-
\(−15,−8\)
Сума двох чисел від'ємна вісімнадцять. Одне число на сорок більше іншого. Знайдіть цифри.
- Відповідь
-
\(−29,11\)
Деякі числові задачі включають послідовні цілі числа. Послідовні цілі числа - це цілі числа, які відразу слідують один за одним. Прикладами послідовних цілих чисел є:
\[\begin{array}{rrrr} 1, & 2, & 3, & 4 \\ −10, & −9, & −8, & −7\\ 150, & 151, & 152, & 153 \end{array}\nonumber\]
Зверніть увагу, що кожне число на одне більше, ніж число, що передує йому. Тому, якщо ми визначимо перше ціле число, як\(n,\) наступне послідовне ціле\(n+1\). Той після цього на один більше\(n+1\), ніж, так він і є\(n+2\).\(n+1+1\)
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
Ми будемо використовувати це позначення для представлення послідовних цілих чисел у наступному прикладі.
Знайти три послідовних цілих числа, сума яких дорівнює\(−54\).
Рішення:
| Крок 1. Прочитайте проблему. | |
| Крок 2. Визначте, що ви шукаєте. | три послідовних цілих числа |
| Крок 3. Назвіть кожне з трьох чисел | Нехай\(n=1^{\text{st}} \text{integer}\). \(n+1=2^{\text{nd}} \text{consecutive integer}\)\(n+2=3^{\text{rd}} \text{consecutive integer}\) |
| Крок 4. Перекласти. Повторюйте як одне речення. Перевести в рівняння. | Сума трьох цілих чисел дорівнює\(−54\).
|
| Крок 5. Розв'яжіть рівняння. Поєднуйте подібні терміни. Відніміть по три з кожного боку. Розділіть кожну сторону на три. | 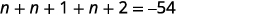 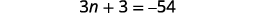 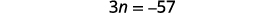 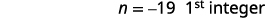
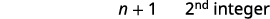 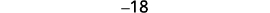 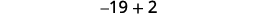 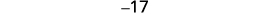 |
| Крок 6. Перевірте. \(\begin{align*} −19+(−18)+(−17) & =−54 \\ −54 & =−54✓ \end{align*}\) | |
| Крок 7. Дайте відповідь на питання. | Три послідовних цілих числа −17, −18 та −19. |
Знайти три послідовних цілих числа, сума яких дорівнює\(−96\).
- Відповідь
-
\(−33,−32,−31\)
Знайти три послідовних цілих числа, сума яких дорівнює\(−36\).
- Відповідь
-
\(−13,−12,−11\)
Тепер, коли ми працювали з послідовними цілими числами, ми будемо розширювати нашу роботу, щоб включити послідовні парні цілі числа і послідовні непарні цілі числа. Послідовні парні цілі числа - це парні цілі числа, які відразу слідують один за одним. Прикладами послідовних парних цілих чисел є:
\[24, 26, 28\nonumber\]
\[−12,−10,−8\nonumber\]
Зверніть увагу, що кожне ціле число на два більше, ніж число, що передує йому. Якщо ми називаємо перший,\(n,\) то наступний\(n+2\). Той, що після цього буде\(n+2+2\) або\(n+4\).
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
Послідовні непарні цілі числа - це непарні цілі числа, які відразу слідують один за одним. Розглянемо послідовні непарні цілі числа 63, 65 і 67.
\[63, 65, 67\nonumber\]
\[n,n+2,n+4\nonumber\]
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
Чи здається дивним додати два (парне число), щоб отримати наступне непарне число? Чи отримуємо ми непарне число або парне число, коли додаємо 2 до 3? до 11? до 47?
Незалежно від того, чи запитує проблема послідовних парних чисел або непарних чисел, вам не потрібно робити нічого іншого. Візерунок залишається тим самим - щоб перейти до наступного непарного або наступного парного цілого числа, додайте два.
Знайдіть три послідовних парних цілих числа, сума яких дорівнює\(120\).
Рішення:
| Крок 1. Прочитайте проблему. | |
| Крок 2. Визначте, що ви шукаєте. | три послідовних парних цілих чисел |
| Крок 3. Назвіть кожне з трьох чисел |
Нехай\(n = 1^{\text{st}} \text{consecutive even integer}\). \(n + 2 = 2^{\text{nd}} \text{consecutive even integer}\). \(n + 4 = 3^{\text{rd}} \text{consecutive even integer}\). |
| Крок 4. Перекласти.
Повторюйте як одне речення. Перевести в рівняння. |
Сума трьох парних цілих чисел дорівнює 120 \(n + n + 2 + n + 4 = 120\) |
| Крок 5. Розв'яжіть рівняння.
Поєднуйте подібні терміни. Відніміть по три з кожного боку. Розділіть кожну сторону на три. |
\(n + n + 2 + n + 4 = 120\) \(\begin{aligned} &{3n+6=120} \\ &{3n=114} \\ &{n=38} &{1^\text{st} \text{integer}}\end{aligned}\) \(\begin{aligned} &{n+2} & &{2^\text{nd} \text{integer}}\\ &{38+2} \\ &{40} \end{aligned}\) \(\begin{aligned} &{n+2} & &{3^\text{rd} \text{integer}}\\ &{38+4} \\ &{42} \end{aligned}\) |
| Крок 6. Перевірте. \(\begin{align*} 38 + 40 + 42 &\overset{?}{=} &120 \nonumber\\ 120 &=& 120 &✓ \nonumber\end{align*}\) | |
| Крок 7. Дайте відповідь на питання. | Три послідовних цілих числа - 38, 40 та 42. |
Знайдіть три послідовних парних цілих числа, сума яких дорівнює 102.
- Відповідь
-
\(32, 34, 36\)
Знайдіть три послідовних парних цілих числа, сума яких дорівнює\(−24\).
- Відповідь
-
\(−10,−8,−6\)
Коли числова проблема знаходиться в контексті реального життя, ми все ще використовуємо ті самі стратегії, які ми використовували для попередніх прикладів.
Сімейна пара разом заробляє 110 000 доларів на рік. Дружина заробляє на 16 000 доларів менше, ніж в два рази більше, ніж заробляє чоловік. На чому заробляє чоловік?
Рішення:
| Крок 1. Прочитайте проблему. | |
| Крок 2. Визначте, що ви шукаєте. | Скільки заробляє чоловік? |
| Крок 3. Назвіть кожне з трьох чисел |
Нехай\(h=\text{the amount the husband earns}\). |
| Крок 4. Перекласти.
Повторюйте проблему в одному реченні з усією важливою інформацією. Перевести в рівняння. |
\(2h−16,000=\text{the amount the wife earns}.\)Разом чоловік і дружина заробляють 110 000 доларів. \(h+2h−16,000=110,000\) |
| Крок 5. Розв'яжіть рівняння.
Поєднуйте подібні терміни. Додайте 16 000 з обох сторін і спростіть. Розділіть кожну сторону на три. |
\(h+2h−16,000=110,000\) \(\begin{aligned} &{3h−16,000=110,000} \\ &{3h=126,000} \\ &{h=42,000} &{\text{amount husband earns}} \end{aligned}\) \(\begin{aligned} &{2h−16,000} &{\text{ amount wife earns}} \\ &{2(42,000)−16,000} \\ &{84,000−16,000} \\ &{68,000} \end{aligned}\) |
| Крок 6. Перевірте. Якщо дружина заробляє 68 000 доларів, а чоловік заробляє 42 000 доларів, це 110 000 доларів? Так! | |
| Крок 7. Дайте відповідь на питання. | Чоловік заробляє 42 000 доларів на рік. |
За даними Національної асоціації автомобільних дилерів, середня вартість автомобіля в 2014 році склала $28,400. Це було на 1600 доларів менше, ніж у шість разів дорожче в 1975 році. Якою була середня вартість автомобіля в 1975 році?
- Відповідь
-
Середня вартість склала 5 000 доларів.
Дані перепису населення США показують, що медіана ціна нового будинку в США в листопаді 2014 року становила $280,900. Це було на 10 700 доларів більше, ніж у 14 разів більше ціни в листопаді 1964 року. Якою була середня ціна нового будинку в листопаді 1964 року?
- Відповідь
-
Медіана ціна склала $19,300.
Вирішити відсоток додатків
Існує кілька методів вирішення відсоткових рівнянь. В алгебрі найпростіше, якщо ми просто переведемо англійські речення в алгебраїчні рівняння, а потім вирішимо рівняння. Обов'язково змініть заданий відсоток на десятковий, перш ніж використовувати його в рівнянні.
Перекладіть і вирішуйте:
- Яке число 45% з 84?
- 8.5% від якої суми становить $4.76?
- 168 - це який відсоток з 112?
Рішення:
а.
 |
|
| Перевести на алгебру. Нехай n = число. | 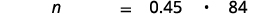 |
| Помножити. | 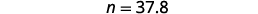 |
| 37,8 становить 45% з 84. |
б.
 |
|
| Перекласти. Нехай\(n =\) сума. | 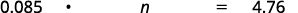 |
| Помножити. | 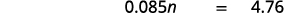 |
| Розділіть обидві сторони на 0,085 і спростіть. |  |
| 8.5% від $56 - це $4.76 |
c.
| Нас просять знайти відсотки, тому ми повинні мати свій результат у відсотковій формі. |  |
| Перевести на алгебру. Нехай\(p = \) відсоток. | 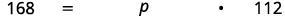 |
| Помножити. |  |
| Розділіть обидві сторони на 112 і спростіть. | .jpg) |
| Перетворити на відсотки. |  |
| 168 - це 150% з 112. |
Перекладіть і вирішуйте:
- Яке число 45% від 80?
- 7,5% від якої суми становить $1.95?
- 110 - це який відсоток від 88?
- Відповідь
-
а. 36 б. $26 с.\(125 \% \)
Перекладіть і вирішуйте:
- Яке число 55% від 60?
- 8.5% від якої суми становить $3.06?
- 126 - це який відсоток від 72?
- Відповідь
-
а. 33 б. $36 с.\(175 \% \)
Тепер, коли ми маємо стратегію вирішення проблем, на яку слід посилатися, і ми практикуємо рішення базових відсоткових рівнянь, ми готові вирішувати відсоткові додатки. Обов'язково запитайте себе, чи має сенс ваша остаточна відповідь - оскільки багато програм, які ми вирішимо, стосуються повсякденних ситуацій, ви можете покластися на власний досвід.
На етикетці йогурту Одрі говорилося, що одна порція забезпечує 12 грамів білка, що становить 24% від рекомендованої добової кількості. Яка загальна рекомендована добова кількість білка?
Рішення:
| Що вас просять знайти? | Яка загальна кількість білка рекомендується? |
| Виберіть змінну для її представлення. | Нехай\(a=\) загальна кількість білка. |
| Напишіть речення, яке дає інформацію, щоб знайти її. | 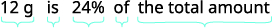 |
| Перевести в рівняння. |  |
| Вирішити. |  |
| Перевірте: Чи має це сенс? Так, 24% - це приблизно\(\frac{1}{4}\) від загальної кількості, а 12 - близько\(\frac{1}{4}\) 50. | |
| Напишіть повне речення, щоб відповісти на питання. | Кількість білка, яке рекомендується, становить 50 г. |
Одна порція пшеничного квадратного злаку містить 7 грам клітковини, що становить 28% від рекомендованої добової кількості. Яка загальна рекомендована добова кількість клітковини?
- Відповідь
-
25 грам
Одна порція рисової крупи містить 190 мг натрію, що становить 8% від рекомендованої добової кількості. Яка загальна рекомендована добова кількість натрію?
- Відповідь
-
2,375 мг
Не забудьте поставити відповідь у запитувану форму. У наступному прикладі шукаємо відсотки.
Вероніка планує приготувати кекси з міксу. На упаковці написано, що кожен кекс буде 240 калорій, а 60 калорій - з жиру. Який відсоток від загальної кількості калорій припадає на жир?
Рішення:
| Що вас просять знайти? | Який відсоток від загальної кількості калорій становить жир? |
| Виберіть змінну для її представлення. | Нехай\(p=\) відсоток жиру. |
| Напишіть речення, яке дає інформацію, щоб знайти її. |  |
| Переведіть речення в рівняння. |  |
| Помножити. |  |
| Розділіть обидві сторони на 240. |  |
| Викладіть у відсоткову форму. |  |
| Перевірте: чи є в цьому сенс? Так,\(25 \% \) одна четверта; 60 - одна четверта з 240. Отже, має\(25 \%\) сенс. | |
| Напишіть повне речення, щоб відповісти на питання. | Із загальної кількості калорій в кожному кексі,\(25 \%\) є жир. |
Mitzi отримав кілька вишуканих тістечок в подарунок. Обгортка сказала, що кожен 28% домовик був 480 калорій, і мав 240 калорій жиру. Який відсоток загальної кількості калорій в кожному брауні надходить від жиру? Округляйте відповідь до найближчого цілого відсотка.
- Відповідь
-
50%
Суміш Рікардо планує використовувати для приготування тістечок, говорить про те, що кожен будинковий складе 190 калорій, а 76 калорій - з жиру. Який відсоток від загальної кількості калорій припадає на жир? Округляйте відповідь до найближчого цілого відсотка.
- Відповідь
-
40%
Часто важливо в багатьох галузях - бізнесі, науці, поп-культурі - говорити про те, наскільки сума збільшилася або зменшилася за певний проміжок часу. Це збільшення або зменшення, як правило, виражається у відсотках і називається відсотковою зміною.
Щоб знайти зміну відсотків, спочатку знаходимо суму зміни, знайшовши різницю нової суми та початкової суми. Потім знаходимо, який відсоток становить сума зміни від початкової суми.
- Знайти суму змін.
\[\text{change}= \text{new amount}−\text{original amount}\]
- Знайдіть, який відсоток становить сума зміни від початкової суми.
зміна - це який відсоток від початкової суми?
Нещодавно губернатор Каліфорнії запропонував підвищити плату за коледж громади з 36 доларів за одиницю до 46 доларів за одиницю. Знайдіть відсоток зміни. (Округлити до найближчої десятої частки відсотка.)
Рішення:
| Знайти суму змін. | \(46−36=10\) |
| Знайдіть відсоток. | Зміна - це який відсоток від початкової суми? |
| Нехай\(p=\) відсоток. |  |
| Перевести на рівняння. | 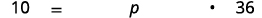 |
| Спростити. | \(10=36 p\) |
| Розділіть обидві сторони на 36. | \(0.278 \approx p\) |
| Змінити на відсоткову форму; округлити до найближчої десятої | \(27.8 \% \approx p\) |
| Напишіть повне речення, щоб відповісти на питання. | Нові збори приблизно\(27.8 \% \) збільшуються в порівнянні зі старими комісіями. |
| Не забудьте округлити поділ до найближчої тисячної, щоб округлити відсоток до найближчої десятої. | |
Знайдіть відсоток зміни. (Округлити до найближчої десятої частки відсотка.) У 2011 році IRS збільшила франшизу вартість пробігу до 55,5 центів з 51 цента.
- Відповідь
-
\(8.8 \% \)
Знайдіть відсоток зміни. (Округлити до найближчої десятої частки відсотка.) У 1995 році стандартна вартість проїзду на автобусі в Чикаго становила $1,50. У 2008 році стандартна вартість проїзду на автобусі становила 2,25.
- Відповідь
-
\(50%\)
Додатки знижки та націнки дуже поширені в роздрібних налаштуваннях.
Коли ви купуєте товар у продажу, початкова ціна була знижена на деяку суму в доларах. Ставка дисконтування, зазвичай дається у відсотках, використовується для визначення суми знижки. Для визначення суми знижки множимо ставку дисконту на початкову ціну.
Ціна, яку роздрібний продавець платить за товар, називається початковою вартістю. Потім роздрібний продавець додає націнку до початкової вартості, щоб отримати прейскурантну ціну, ціну, за яку він продає товар. Націнка зазвичай розраховується як відсоток від початкової вартості. Щоб визначити суму націнки, помножте ставку націнки на початкову вартість.
\[ \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\]
Ціна продажу завжди повинна бути меншою за початкову ціну.
\[\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\]
Ціна за прейскурантом завжди повинна бути більше початкової вартості.
Художня галерея Ліама купила картину за оригінальною вартістю 750 доларів. Ліам відзначив ціну вгору на 40%. Знайти
- сума націнки і
- прейскурантна ціна картини.
Рішення:
а.
| Визначте те, що вас попросять знайти, і виберіть змінну для його представлення. | Яка сума націнки? Нехай\(m=\) сума націнки. |
| Напишіть речення, яке дає інформацію, щоб знайти її. | 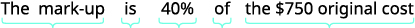 |
| Перевести в рівняння. |  |
| Розв'яжіть рівняння. |  |
| Напишіть повне речення. | Націнка на картину склала 300 доларів. |
| Визначте те, що вас попросять знайти, і виберіть змінну для його представлення. | Що таке прейскурант? Нехай\(p=\) прейскурант прайс. |
| Напишіть речення, яке дає інформацію, щоб знайти її. |  |
| Перевести в рівняння. | 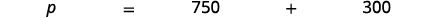 |
| Розв'яжіть рівняння. |  |
| Перевірте. | Чи є прейскурантна ціна більше, ніж початкова вартість? Це $1,050 більше, ніж $750? Так. |
| Напишіть повне речення. | Прайс-лист картини склав 1 050 доларів. |
Знайти a. кількість націнки і б. ціна прейскуранта: музичний магазин Джима купив гітару за первісною вартістю $1200. Джим відзначив ціну вгору на 50%.
- Відповідь
-
a. 600 мільярдів доларів 1800 доларів
Знайдіть a. суму націнки та б. ціна за прейскурантом: Магазин автоперепродажу купив Pablo Toyota за $8500. Вони відзначили ціну вгору на 35%.
- Відповідь
-
а. $2,975 млрд. $11,475
Вирішіть прості програми для інтересів
Інтерес є частиною нашого повсякденного життя. Від відсотків, зароблених на наших заощадженнях, до відсотків, які ми сплачуємо по автокредиту або заборгованості по кредитній карті, ми всі маємо певний досвід з відсотками в нашому житті.
Сума грошей, яку ви спочатку вносите в банк, називається основною,\(P,\) і банк платить вам відсотки.\(I.\) Коли ви берете кредит, ви сплачуєте відсотки від суми, яку ви позичаєте, також називається основною.
У будь-якому випадку відсотки обчислюються як певний відсоток основної суми, званий процентною ставкою,\(r.\) процентна ставка зазвичай виражається у відсотках на рік, і обчислюється за допомогою десяткового еквівалента відсотків. Змінна\(t,\) (для часу) являє собою кількість років, в яких гроші зберігаються або позичаються.
Відсотки розраховуються як прості відсотки або складні відсотки. Тут ми будемо використовувати прості відсотки.
Якщо сума грошей, яка\(P,\) називається основною, вкладається або позичається на період\(t\) років за річною процентною\(r,\) ставкою, сума відсотків,\(I,\) зароблених або сплачених становить
\[ \begin{array}{ll} I=Prt \; \; \; \; \; \; \; \; \; \; \; \; \text{where} & { \begin{align*} I &= \text{interest} \\ P &= \text{principal} \\ r &= \text{rate} \\ t &= \text{time} \end{align*}} \end{array}\]
Відсотки, зароблені або виплачені за цією формулою, називають простими відсотками.
Формула, яку ми використовуємо для обчислення відсотків, є\(I=Prt\). Для використання формули підставляємо в значення змінних, які задані, а потім вирішуємо для невідомої змінної. Можливо, буде корисно впорядкувати інформацію в діаграмі.
Арелі інвестувала основний капітал у розмірі 950 доларів на свій банківський рахунок, який заробив прості відсотки за процентною ставкою 3%. Скільки відсотків вона заробила за п'ять років?
Рішення:
\( \begin{aligned} I & = \; ? \\ P & = \; \$ 950 \\ r & = \; 3 \% \\ t & = \; 5 \text{ years} \end{aligned}\)
\(\begin{array}{ll} \text{Identify what you are asked to find, and choose a} & \text{What is the simple interest?} \\ \text{variable to represent it.} & \text{Let } I= \text{interest.} \\ \text{Write the formula.} & I=Prt \\ \text{Substitute in the given information.} & I=(950)(0.03)(5) \\ \text{Simplify.} & I=142.5 \\ \text{Check.} \\ \text{Is } \$142.50 \text{ a reasonable amount of interest on } \$ \text{ 950?} \; \;\;\;\;\; \;\;\;\;\;\; \\ \text{Yes.} \\ \text{Write a complete sentence.} & \text{The interest is } \$ \text{142.50.} \end{array}\)
Наталі внесла $12,500 на свій банківський рахунок, де вона заробить 4% простих відсотків. Скільки відсотків заробить Наталі за п'ять років?
- Відповідь
-
Він запрацює 2500 доларів.
Сусана інвестувала основний капітал у розмірі 36 000 доларів на свій банківський рахунок, який заробив прості відсотки за процентною ставкою 6,5%. Скільки відсотків вона заробила за три роки?
- Відповідь
-
Вона заробила 7 020 доларів.
Можуть бути випадки, коли ми знаємо суму відсотків, зароблених за певним принципалом протягом певного періоду часу, але ми не знаємо ставки.
Ханг позичив у батьків 7500 доларів, щоб оплатити навчання. За п'ять років вона заплатила їм 1,500 відсотків на додаток до 7500 доларів, які вона позичила. Якою була ставка простих відсотків?
Рішення:
\( \begin{aligned} I & = \; \$ 1500 \\ P & = \; \$ 7500 \\ r & = \; ? \\ t & = \; 5 \text{ years} \end{aligned}\)
\ (\ text {Визначте, що вас просять знайти,}\ qquad\ quad\ text {Що таке ставка простого відсотка?} \\
\ begin {align*}
&\ text {і виберіть змінну для її представлення.} &\ text {Нехай} r\; &=\;\ text {процентна ставка}\\
&\ text {Напишіть формулу.} & I\; &=\; Prt\\
&\ text {Замістити у вказану інформацію.} & 1500\; &=\; (7,500) r (5)\\
&\ text {Множення.} & 1500\; &=\; 37,500r\\
&\ text {Розділити.} & 0.04\; &=\; r\\
&\ text {Змінити на відсоткову форму} & r\; &=\; 4\%
\ end {align*}\)
Перевірте.
\ (\ begin {вирівнювати*} I\; &=\; Prt\\
1500\; &\ stackrel {?} {=}\; (7,500) (0.04) (5)\\
1500\; &=\; 1500 ✓\ кінець {вирівнювати*}\)
Напишіть повне речення. Ставка відсотка склала\(4\%.\)
Джим позичив своїй сестрі 5000 доларів, щоб допомогти їй купити будинок. За три роки вона заплатила йому 5000 доларів, плюс 900 доларів. Якою була ставка простих відсотків?
- Відповідь
-
Ставка простого відсотка склала 6%.
Лорен позичив своєму братові 3000 доларів, щоб допомогти йому придбати автомобіль. За чотири роки його брат виплатив йому 3,000 доларів плюс 660 доларів у відсотках. Якою була ставка простих відсотків?
- Відповідь
-
Ставка простого відсотка склала 5,5%.
У наступному прикладі нас просять знайти принципалу—суму в борг.
Нова заява Шона про кредит на автомобіль заявив, що він заплатить $4,866,25 відсотки від простої процентної ставки 8,5% протягом п'яти років. Скільки він позичив, щоб купити свою нову машину?
Рішення:
\( \begin{aligned} I & = \; 4,866.25 \\ P & = \; ? \\ r & = \; 8.5 \% \\ t & = \; 5 \text{ years} \end{aligned}\)
\ (\ text {Визначте, що вас просять знайти,}\ qquad\ quad\ text {Яка сума позики (основна сума)?} \\
\ begin {align*}
&\ text {і виберіть змінну для її представлення.} &\ text {Нехай} P\; &=\;\ текст {основний запозичений}\\
&\ текст {Напишіть формулу.} & I\; &=\; Prt\\
&\ text {Замістити у вказану інформацію.} & 4,866.25\; &=\; P (0.085) (5)\\
&\ text {Множення.} & 4,866.25\; &=\; 0.425P\\
&\ текст {Розділити.} & 11,450\; &=\; P
\ end {вирівнювати*}\)
Перевірте.
\ (\ begin {вирівнювати*} I\; &=\; Prt\\
4,866.25\; &\ stackrel {?} {=}\; (11,450) (0.085) (5)\\
4,866.25\; &=\; 4,866.25 ✓\ кінець {вирівнювати*}\)
Напишіть повне речення. Принципал був\($11,450.\)
Едуардо помітив, що в його нових документах про автокредит зазначено, що з простою процентною ставкою 7,5% він заплатить 6,596,25 доларів відсотків протягом п'яти років. Скільки він позичив, щоб заплатити за свою машину?
- Відповідь
-
Він заплатив 17 590 доларів.
За п'ять років банківський рахунок Глорії заробив 2400 доларів відсотків під 5% простих відсотків. Скільки вона внесли на рахунок?
- Відповідь
-
Вона депонувала $9600.
Отримайте доступ до цього онлайн-ресурсу для отримання додаткової інструкції та практики з використанням стратегії вирішення проблем.
- Початок арифметичних задач
Ключові концепції
- Як використовувати стратегію вирішення проблем для проблем Word
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте, що ви шукаєте.
- Назвіть те, що ви шукаєте. Виберіть змінну для представлення цієї кількості.
- Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в рівняння алгебри.
- Розв'яжіть рівняння, використовуючи правильні методи алгебри.
- Перевірте відповідь у проблемі, щоб переконатися, що це має сенс.
- Відповісти на питання повним реченням.
- Як знайти відсоток зміни
- Знайти суму зміни
\(\text{change}=\text{new amount}−\text{original amount}\)
- Знайдіть, який відсоток становить сума зміни від початкової суми.
\(\text{change is what percent of the original amount?}\)
- Знайти суму зміни
- \( \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\)
- \(\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\)
- Якщо сума грошей, яка\(P,\) називається основною, вкладається або позичається на термін t років під річну процентну ставку\(r,\), сума відсотків,\(I,\) зароблених або сплачених становить:\[\begin{aligned} &{} &{} &{I=interest} \nonumber\\ &{I=Prt} &{\text{where} \space} &{P=principal} \nonumber\\ &{} &{\space} &{r=rate} \nonumber\\ &{} &{\space} &{t=time} \nonumber \end{aligned}\]