9.5: Графічні параболи
- Page ID
- 58206
Цілі навчання
- Графік параболи.
- Знайдіть перехоплення і вершину параболи.
- Знайдіть вершину параболи, заповнивши квадрат.
Графік квадратного рівняння
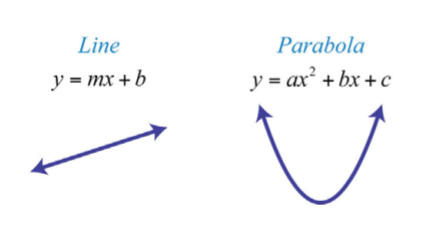
Ми знаємо, що будь-яке лінійне рівняння з двома змінними може бути записано у вигляді\(y=mx+b\) і що його графік є лінією. У цьому розділі ми побачимо, що будь-яке квадратне рівняння виду\(y=ax^{2}+bx+c\) має вигнутий графік, який називається параболою.
.png)
Дві точки визначають будь-яку лінію. Однак, оскільки парабола вигнута, ми повинні знайти більше двох точок. У цьому тексті ми визначимо як мінімум п'ять пунктів як засіб для виготовлення прийнятного ескізу. Для початку ми графуємо нашу першу параболу шляхом побудови точок. Задано квадратне рівняння виду\(y=ax^{2}+bx+c\), x є незалежною змінною, а y - залежною змінною. Виберіть деякі значення для x, а потім визначте відповідні y -значення. Потім намалюйте точки і накидайте графік.
Приклад\(\PageIndex{1}\)
Графік шляхом побудови точок:
\(y=x^{2}-2x-3\)
Рішення:
У цьому прикладі оберіть значення x {−2, −1, 0, 1, 2, 3, 4} і обчислите відповідні y -значення.
.png)
Побудуйте ці точки і визначте форму графіка.
Відповідь:
.png)
При побудові графіків ми хочемо включити певні спеціальні точки на графіку. Перехоплення y - це точка, де графік перетинає вісь y. X -перехоплення - це точки, де графік перетинає вісь x. Вершина - це точка, яка визначає мінімум або максимум графа. Нарешті, лінія симетрії (її ще називають віссю симетрії) - це вертикальна лінія через вершину, про яку парабола симетрична.
.png)
Для будь-якої параболи знайдемо вершину і y -перехоплення. Крім того, якщо x -перехоплення існують, то ми також хочемо визначити їх. Ворожіння на х -значеннях цих спеціальних точок не є практичним, тому ми розробимо прийоми, які полегшать їх пошук. Багато з цих методів будуть широко використовуватися, коли ми прогресуємо в нашому вивченні алгебри. Задано квадратне рівняння виду\(y=ax^{2}+bx+c\), знайдіть y -перехоплення, встановивши x=0 та розв'язавши. Загалом\(y=a(0)^{2}+b(0)+c=c\), і у нас є
\ (\ color {Cerulean} {y-перехоплення}
\ [(0, с]\)
Далі нагадаємо, що х -перехоплення, якщо вони існують, можна знайти, встановивши y=0. Роблячи це, ми маємо\(0=a^{2}+bx+c\), який має загальні рішення, наведені квадратичною формулою,\(x=\frac{−b±\sqrt{b^{2}−4ac}}{2a}\). Тому Х-перехоплення мають такий загальний вигляд:
\(\color{Cerulean}{x-intercepts}\)
Використовуючи те, що парабола симетрична, ми можемо визначити вертикальну лінію симетрії за допомогою x -перехоплень. Для цього знаходимо x -значення посередині між x -перехопленнями, взявши середнє значення наступним чином:
Тому лінією симетрії є вертикальна лінія:
\(\color{Cerulean}{Line\:of\:symmetry}\)
\[x=-\frac{b}{2 a}\]
Ми можемо використовувати лінію симетрії, щоб знайти x -значення вершини. Етапи побудови графіка параболи описані в наступному прикладі.
Приклад\(\PageIndex{2}\)
Графік:
Рішення
Крок 1: Визначте y -перехоплення. Для цього задаємо x = 0 і вирішуємо для y.
Y -перехоплення є (0, 3).
Крок 2: Визначте x -перехоплення. Для цього задаємо y = 0 і вирішуємо для x.
\(\begin{array}{rlr}{x+3} & {=0} & {\text { or }} & {x-1=0} \\ {x} & {=-3} & {} & {x=1}\end{array}\)
Тут при y = 0 отримуємо два рішення. Існує два x -перехоплення, (−3, 0) та (1, 0).
Крок 3: Визначаємо вершину. Один із способів зробити це - використовувати рівняння для лінії симетрії\(x=\frac{-b}{2 a}\), щоб знайти x -значення вершини. У цьому прикладі a = −1 і b = −2:
Заставте −1 у вихідне рівняння, щоб знайти відповідне значення y.
Вершина дорівнює (−1, 4).
Крок 4: Визначте зайві точки так, щоб у нас було принаймні п'ять точок для побудови сюжету. У цьому прикладі буде достатньо одного іншого пункту. Виберіть x = −2 і знайдіть відповідне значення y.
.png)
Наш п'ятий пункт - (-2,3).
Крок 5: Намалюйте точки та намалюйте графік. Нагадаємо, пункти, які ми знайшли, є
| y-перехоплення: | (0,3) |
|---|---|
| X-перехоплення: | (-3,0) і (1,0) |
| Вершина: | (-1,4) |
| Додаткова точка: | (-2,3) |
Відповідь:
.png)
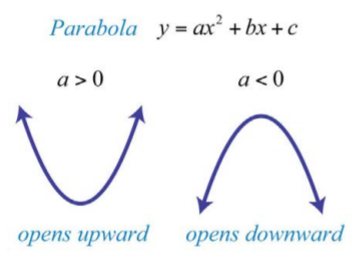
Парабола відкривається вниз. Загалом, використовуйте провідний коефіцієнт, щоб визначити, чи відкривається парабола вгору або вниз. Якщо провідний коефіцієнт негативний, як в попередньому прикладі, то парабола відкривається вниз. Якщо провідний коефіцієнт позитивний, то парабола відкривається вгору.
.png)
Всі квадратні рівняння виду\(y=ax^{2}+bx+c\) мають параболічні графи з y -перехопленням (0, в ). Однак не всі параболи мають х перехоплень.
Приклад\(\PageIndex{3}\)
Графік:
\(y=2x^{2}+4x+5\)
Рішення:
Оскільки провідний коефіцієнт 2 позитивний, зверніть увагу, що парабола відкривається вгору. Тут c = 5 і y -перехоплення є (0, 5). Щоб знайти x -перехоплення, встановіть y = 0.
\(\begin{array}{l}{y=2 x^{2}+4 x+5} \\ {0=2 x^{2}+4 x+5}\end{array}\)
В даному випадку a = 2, b = 4, а c = 5. Використовуйте дискримінант для визначення кількості та типу розв'язків.
Оскільки дискримінант негативний, робимо висновок, що реальних рішень немає. Оскільки реальних рішень немає, немає х -перехоплень. Далі визначаємо x -значення вершини.
Враховуючи, що x -значення вершини дорівнює −1, підставляємо до вихідного рівняння, щоб знайти відповідне y -значення.
\(\begin{aligned} y &=2 x^{2}+4 x+5 \\ &=2(\color{OliveGreen}{-1}\color{black}{)}^{2}+4(\color{OliveGreen}{-1}\color{black}{)}+5 \\ &=2-4+5 \\ &=3 \end{aligned}\)
Вершина дорівнює (−1, 3). Поки що у нас всього два пункти. Щоб визначити ще три, оберіть декілька x -значень по обидві сторони від лінії симетрії, x = −1. Тут ми вибираємо x -values −3, −2 та 1.
.png)
Підводячи підсумок, ми маємо
| y-перехоплення: | (0,5) |
|---|---|
| Х-перехоплює: | Жоден |
| Вершина: | (-1,3) |
| Додаткові бали | (-3,11), (-2,5), (1,11) |
Побудуйте точки і накидайте графік.
Відповідь:
.png)
Приклад\(\PageIndex{4}\)
Графік:
Рішення
Зауважте, що a = −2: парабола відкривається вниз. Оскільки c = −18, перехоплення y дорівнює (0, −18). Щоб знайти x -перехоплення, встановіть y = 0.
Вирішити шляхом факторингу.
\(\begin{array}{rrr}{x-3=0} & {\text { or }} & {x-3=0} \\ {x=3} && {x=3}\end{array}\)
Тут x = 3 - це подвійний корінь, тому існує лише один х -перехоплення, (3, 0). З вихідного рівняння a = −2, b = 12, а c = −18. X -значення вершини можна обчислити наступним чином:
\(\begin{aligned} x &=\frac{-b}{2 a} \\ &=\frac{-(\color{OliveGreen}{12}\color{black}{)}}{2(\color{OliveGreen}{-2}\color{black}{)}} \\ &=\frac{-12}{-4} \\ &=3 \end{aligned}\)
Враховуючи, що x -значення вершини дорівнює 3, підставляємо в вихідне рівняння, щоб знайти відповідне y -значення.
Отже, вершина є (3, 0), яка буває тією ж точкою, що і x -перехоплення. Поки що у нас всього два пункти. Щоб визначити ще три, виберіть деякі x -значення по обидва боки від лінії симетрії, x = 3 в даному випадку.
Виберіть x -значення 1, 5 та 6.
Підводячи підсумок, ми маємо
| y-перехоплення: | (0, -18) |
|---|---|
| Х-перехоплює: | (3, 0) |
| Вершина: | (3, 0) |
| Додаткові бали: | (1, -8), (5, -8), (6, -18) |
Побудуйте точки і накидайте графік.
Відповідь:
.png)
Приклад\(\PageIndex{5}\)
Графік:
Рішення:
Оскільки a = 1, парабола відкривається вгору. Крім того, c = −1, тому перехоплення y дорівнює (0, −1). Щоб знайти x -перехоплення, встановіть y = 0.
У цьому випадку вирішуйте за допомогою квадратичної формули з a = 1, b = −2, а c = −1.
Тут ми отримуємо два реальних рішення для x, і таким чином існує два x -перехоплення:
\((1-\sqrt{2}, 0) \quad \text { and } \qquad(1+\sqrt{2}, 0)\)
Приблизні значення за допомогою калькулятора:
\((-0.41,0) \qquad \text { and } \qquad(2.41,0)\)
Використовуйте приблизні відповіді, щоб розмістити впорядковану пару на графіку.
Однак ми представимо точні x -перехоплення на графіку. Далі знайдіть вершину.
\(\begin{aligned} x &=\frac{-b}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2}{2} \\ &=1 \end{aligned}\)
Враховуючи, що x -значення вершини дорівнює 1, підставляємо в вихідне рівняння, щоб знайти відповідне y -значення.
Вершина - (1, -2). Нам потрібен ще один пункт.
Підводячи підсумок, ми маємо
| y-перехоплення: | (0, -1) |
|---|---|
| Х-перехоплює: | \((1-\sqrt{2}, 0)\)і\((1+\sqrt{2}, 0)\) |
| Вершина: | \((1, -2)\) |
| Додаткова точка: | \((2, -1)\) |
Побудуйте точки і накидайте графік.
Відповідь:
.png)
Вправа\(\PageIndex{1}\)
Графік:
\(y=9x^{2}-5\)
- Відповідь
-
.png)
Малюнок\(\PageIndex{14}\)
Пошук максимуму і мінімуму
Часто корисно знайти максимальні та/або мінімальні значення функцій, які моделюють реальні програми. Щоб знайти ці важливі значення, задані квадратичною функцією, ми використовуємо вершину. Якщо провідний коефіцієнт a позитивний, то парабола відкривається вгору і буде мінімальне y -значення. Якщо провідний коефіцієнт a негативний, то парабола відкривається вниз і буде максимальне y -значення.
Приклад\(\PageIndex{6}\)
Визначаємо максимум або мінімум:
\(y=−4x^{2}+24x−35\)
Рішення:
Оскільки a = −4, ми знаємо, що парабола відкривається вниз і буде максимальне y -значення. Щоб його знайти, спочатку знайдемо x -значення вершини.
\(\begin{aligned} x &=-\frac{b}{2 a} \qquad\quad\color{Cerulean}{x-value\:of\:the\:vertex.} \\ &=-\frac{24}{2(-4)}\quad\:\color{Cerulean}{Substitute\:a=-4\:and\:b=24.} \\ &=-\frac{24}{-8} \qquad\:\: \color{Cerulean}{Simplify.} \\ &=3 \end{aligned}\)
Значення x вершини дорівнює 3. Підставте це значення у вихідне рівняння, щоб знайти відповідне y -значення.
Вершина - (3, 1). Тому максимальне значення y дорівнює 1, що виникає при x = 3, як показано нижче:
Примітка
Графік не обов'язковий для відповіді на це питання.
Відповідь:
Максимальний - 1.
Приклад\(\PageIndex{7}\)
Визначаємо максимум або мінімум:
\(y=4x^{2}−32x+62\)
Рішення:
Оскільки a = +4, парабола відкривається вгору і існує мінімальне y -значення. Почніть з пошуку x -значення вершини.
\(\begin{aligned} x &=-\frac{b}{2 a} \\ &=-\color{black}{\frac{\color{OliveGreen}{-32}}{\color{black}{2}(\color{OliveGreen}{4}\color{black}{)}}}\qquad\color{Cerulean}{Substitute\:a=4\:and\:b=-32.} \\ &=-\frac{-32}{8}\qquad\color{Cerulean}{Simplify.} \\ &=4 \end{aligned}\)
Заставте x = 4 у вихідне рівняння, щоб знайти відповідне y -значення.
Вершина дорівнює (4, −2). Отже, мінімальне значення y −2 виникає, коли x = 4, як показано нижче:
Відповідь:
Мінімальний - -2.
Вправа\(\PageIndex{2}\)
Визначаємо максимум або мінімум:
\(y=(x-3)^{2}-9\)
- Відповідь
-
Мінімальним є −9.
Парабола, що відкривається вгору або вниз (на відміну від вбік), визначає функцію і поширюється на невизначений час вправо і вліво, як зазначено стрілками. Тому домен (множина х -значень) складається з усіх дійсних чисел. Однак діапазон (набір y -значень) обмежений y -значенням вершини.
Приклад\(\PageIndex{8}\)
Визначаємо домен і діапазон:
\(y=x^{2}-4x+3\)
Рішення:
По-перше, зауважте, що оскільки a = 1 є позитивним, парабола відкривається вгору. Звідси буде мінімальне y -значення. Щоб знайти це значення, знайдіть x -значення вершини:
\(x=-\frac{b}{2 a}=-\frac{-4}{2(1)}=2\)
Потім підставляємо в рівняння, щоб знайти відповідне y -значення.
Вершина дорівнює (2, −1). Діапазон складається з множини y -значень, більших або рівних мінімальному y -значенню −1.
Відповідь:
Домен: R =\((-\infty, \infty)\); Діапазон:\([-1, \infty)\)
Приклад\(\PageIndex{9}\)
Висота в ногах снаряда задається функцією\(h(t)=−16t^{2}+72t\), де t представляє час у секундах після запуску. Якої максимальної висоти досягається снарядом?
Рішення:
Тут a=−16, і парабола відкривається вниз. Тому y -значення вершини визначає максимальну висоту. Почніть з пошуку x -значення вершини:
\(x=-\frac{b}{2 a}=-\frac{72}{2(-16)}=\frac{72}{32}=\frac{9}{4}\)
Максимальна висота відбудеться через 9/4 = 2¼ секунди. Підставте цей час у функцію, щоб визначити досягнуту висоту.
\(\begin{aligned} h\left(\frac{9}{4}\right) &=-16\left(\frac{9}{4}\right)^{2}+72\left(\frac{9}{4}\right) \\ &=-16\left(\frac{81}{16}\right)+72\left(\frac{9}{4}\right) \\ &=-81+162 \\ &=81 \end{aligned}\)
Відповідь:
Максимальна висота снаряда - 81 фут.
Пошук вершини шляхом завершення квадрата
У цьому розділі ми продемонструємо альтернативний підхід до знаходження вершини. Будь-яке квадратне рівняння\(y=ax^{2}+bx+c\) можна переписати у вигляді
\[y=a(x-h)^{2}+k\]
У такому вигляді вершина дорівнює (h, k).
Приклад\(\PageIndex{10}\)
Визначаємо вершину:
\(y=-4(x-3)^{2}+1\)
Рішення:
Коли рівняння знаходиться в такому вигляді, ми можемо прочитати вершину безпосередньо з рівняння.
\(\begin{array}{l}{y=\:a\:(\:x-h)^{2}+k} \\ \color{Cerulean}{\qquad\qquad\quad\downarrow\quad\:\:\downarrow} \\ {y=-4(x-3)^{2}+1}\end{array}\)
Тут h =3 і k =1.
Відповідь:
Вершина - (3, 1).
Приклад\(\PageIndex{11}\)
Визначаємо вершину:
\(y=2(x+3)^{2}-2\)
Рішення:
Перепишіть рівняння наступним чином перед визначенням h і k.
\(\begin{array}{l}{y=\:a\:(\:x\:-h)^{2}\:\:\:\:+\:\:\:k} \\ \color{Cerulean}{\qquad\qquad\quad\:\downarrow\qquad\quad\downarrow} \\ {y=2(x-(-3))^{2}+(-2)}\end{array}\)
Тут h =-3 і k =-2.
Відповідь:
Вершина - (-3, -2).
Часто рівняння не дається в такому вигляді. Щоб отримати таку форму, заповніть квадрат.
Приклад\(\PageIndex{12}\)
Перепишіть за\(y=a(x−h)^{2}+k\) формою і визначте вершину:\(y=x^{2}+4x+9\).
Рішення:
Почніть з звільнення місця для постійного терміну, який завершує квадрат.
\(\begin{aligned} y &=x^{2}+4 x+9 \\ &=x^{2}+4 x+\underline\quad+9-\underline\quad\end{aligned}\)
Ідея полягає в тому, щоб додати і відняти значення, яке завершує квадрат\(\frac{b^{2}}{2}\), а потім коефіцієнт. В цьому випадку додаємо і віднімаємо\(\frac{4^{2}}{2} = 2^{2} = 4\).
\(\begin{aligned} y &=x^{2}+4 x+9 \qquad\quad\:\:\:\color{Cerulean}{Add\:and\:subtract\:4.} \\ &=\underbrace{x^{2}+4 x\color{Cerulean}{+4}}_{\text { factor }}+9\color{Cerulean}{-4} \quad\color{Cerulean}{Factor.} \\ &=(x+2)(x+2)+5 \\ &=(x+2)^{2}+5 \end{aligned}\)
Додавання та віднімання одного і того ж значення всередині виразу не змінює його. Робити це еквівалентно додаванню 0. Як тільки рівняння буде в такому вигляді, ми можемо легко визначити вершину.
\(\begin{array}{c}{y=a(x-h)^{2}\:+\:\:k} \\ \color{Cerulean}{\qquad\quad\quad\:\:\downarrow\qquad\downarrow} \\ {y=(x-(-2))^{2}+5}\end{array}\)
Тут h =-2 і k =5.
Відповідь:
Вершина - (-2, 5).
Якщо є провідний коефіцієнт, відмінний від 1, то ми повинні спочатку перерахувати провідний коефіцієнт з перших двох членів триноміала.
Приклад\(\PageIndex{13}\)
Перепишіть за\(y=a(x−h)^{2}+k\) формою і визначте вершину:\(y=2x^{2}−4x+8\).
Рішення:
Оскільки a = 2, множник цього з перших двох членів, щоб завершити квадрат. Залиште місце всередині дужок, щоб додати постійний термін.
Тепер скористайтеся −2, щоб визначити значення, яке завершує квадрат. В даному випадку,\(\frac{(-2)^{2}}{2}=\((-1)^{2}=1\). Додайте і відніміть 1 і множник наступним чином:
У такому вигляді ми легко можемо визначити вершину.
\(\begin{array}{l}{y=a(x-h)^{2}+k} \\ \color{Cerulean}{\qquad\qquad\:\downarrow\quad\:\:\:\downarrow}\\ {y=2(x-1)^{2} \:+6}\end{array}\)
Тут h =1 і k =6.
Відповідь:
Вершина - це (1, 6).
Вправа\(\PageIndex{3}\)
Перепишіть за\(y=a(x-h)^{2}+k\) формою і визначте вершину:
\(y=-2x^{2}-12x+3\).
- Відповідь
-
\(y=-2(x+3)^{2}+21\); вершина:\((-3, 21)\)
Ключові виноси
- Графік будь-якого квадратного рівняння\(y=ax^{2}+bx+c\), де a, b і c - дійсні числа, а a0, називається параболою.
- При побудові графіків параболи знайдіть вершину і y -перехоплення. Якщо x -перехоплення існують, знайдіть їх також. Також обов'язково знайдіть впорядковані парні рішення по обидва боки від лінії симетрії,\(x=\frac{-b^{2}}{a}\).
- Використовуйте провідний коефіцієнт, а, щоб визначити, чи відкривається парабола вгору або вниз. Якщо a позитивний, то він відкривається вгору. Якщо a негативний, то він відкривається вниз.
- Вершина будь-якої параболи має значення x, рівне\(x=\frac{-b^{2}}{a}\). Після знаходження x -значення вершини підставляємо його в вихідне рівняння, щоб знайти відповідне y -значення. Це y -значення є максимумом, якщо парабола відкривається вниз, і це мінімум, якщо парабола відкривається вгору.
- Домен параболи, що відкривається вгору або вниз, складається з усіх дійсних чисел. Діапазон обмежений y -значенням вершини.
- Альтернативним підходом до знаходження вершини є переписування квадратного рівняння у вигляді\(y=a(x−h)^{2}+k\). Коли в такому вигляді вершина дорівнює (h, k) і може бути прочитана безпосередньо з рівняння. Щоб отримати цю форму, візьміть\(y=ax^{2}+bx+c\) і заповніть квадрат.
Вправа\(\PageIndex{4}\) the graph of quadratic equations
Парабола відкривається вгору або вниз? Поясніть.
- \(y=x^{2}−9x+20\)
- \(y=x^{2}−12x+32\)
- \(y=−2x^{2}+5x+12\)
- \(y=−6x^{2}+13x−6\)
- \(y=64−x^{2}\)
- \(y=−3x+9x^{2}\)
- Відповідь
-
1. Вгору
3. Внизу
5. Внизу
Вправа\(\PageIndex{5}\) the graph of quadratic equations
Визначте x - і y -перехоплення.
- \(y=x^{2}+4x−12\)
- \(y=x^{2}−13x+12\)
- \(y=2x^{2}+5x−3\)
- \(y=3x^{2}−4x−4\)
- \(y=−5x^{2}−3x+2\)
- \(y=−6x^{2}+11x−4\)
- \(y=4x^{2}−25\)
- \(y=9x^{2}−49\)
- \(y=x^{2}−x+1\)
- \(y=5x^{2}+15x\)
- Відповідь
-
1. x -перехоплює:\((−6, 0), (2, 0)\); y -перехоплення:\((0, −12)\)
3. x -перехоплює:\((−3, 0), (\frac{1}{2}, 0)\); y -перехоплення:\((0, −3)\)
5. x -перехоплює:\((−1, 0), (\frac{2}{5}, 0)\); y -перехоплення:\((0, 2)\)
7. x -перехоплює:\((−\frac{5}{2}, 0), (\frac{5}{2}, 0)\); y -перехоплення:\((0, −25)\)
9. x -перехоплює: немає; y -перехоплення:\((0, 1)\)
Вправа\(\PageIndex{6}\) the graph of quadratic equations
Знайдіть вершину і лінію симетрії.
- \(y=−x^{2}+10x−34\)
- \(y=−x^{2}−6x+1\)
- \(y=−4x^{2}+12x−7\)
- \(y=−9x^{2}+6x+2\)
- \(y=4x^{2}−1\)
- \(y=x^{2}−16\)
- Відповідь
-
1. Вершина:\((5, −9)\); лінія симетрії:\(x=5\)
3. Вершина:\((\frac{3}{2}, 2)\); лінія симетрії:\(x= \frac{3}{2}\)
5. Вершина:\((0, −1)\); лінія симетрії:\(x=0\)
Вправа\(\PageIndex{7}\) the graph of quadratic equations
Графік. Знайдіть вершину і y -перехоплення. Крім того, знайдіть x -перехоплення, якщо вони існують.
- \(y=x^{2}−2x−8\)
- \(y=x^{2}−4x−5\)
- \(y=−x^{2}+4x+12\)
- \(y=−x^{2}−2x+15\)
- \(y=x^{2}−10x\)
- \(y=x^{2}+8x\)
- \(y=x^{2}−9\)
- \(y=x^{2}−25\)
- \(y=1−x^{2}\)
- \(y=4−x^{2}\)
- \(y=x^{2}−2x+1\)
- \(y=x^{2}+4x+4\)
- \(y=−4x^{2}+12x−9\)
- \(y=−4x^{2}−4x+3\)
- \(y=x^{2}−2\)
- \(y=x^{2}−3\)
- \(y=−4x^{2}+4x−3\)
- \(y=4x^{2}+4x+3\)
- \(y=x^{2}−2x−2\)
- \(y=x^{2}−6x+6\)
- \(y=−2x^{2}+6x−3\)
- \(y=−4x^{2}+4x+1\)
- \(y=x^{2}+3x+4\)
- \(y=−x^{2}+3x−4\)
- \(y=−2x^{2}+3\)
- \(y=−2x^{2}−1\)
- \(y=2x^{2}+4x−3\)
- \(y=3x^{2}+2x−2\)
- Відповідь
-
1.
.png)
Малюнок\(\PageIndex{18}\) 3.
.png)
Малюнок\(\PageIndex{19}\) 5.
.png)
Малюнок\(\PageIndex{20}\) 7.
.png)
Малюнок\(\PageIndex{21}\) 9.
.png)
Малюнок\(\PageIndex{22}\) 11.
.png)
Малюнок\(\PageIndex{23}\) 13.
.png)
Малюнок\(\PageIndex{24}\) 15.
.png)
Малюнок\(\PageIndex{25}\) 17.
.png)
Малюнок\(\PageIndex{26}\) 19.
.png)
Малюнок\(\PageIndex{27}\) 21.
.png)
Малюнок\(\PageIndex{28}\) 23.
.png)
Малюнок\(\PageIndex{29}\) 25.
.png)
Малюнок\(\PageIndex{30}\) 27.
.png)
Малюнок\(\PageIndex{31}\)
Вправа\(\PageIndex{8}\) maximum or minimum
Визначте максимальне або мінімальне y -значення.
- \(y=−x^{2}−6x+1\)
- \(y=−x^{2}−4x+8\)
- \(y=25x^{2}−10x+5\)
- \(y=16x^{2}−24x+7\)
- \ (y=−x^ {2}
- \(y=1−9x^{2}\)
- \(y=20x−10x^{2}\)
- \(y=12x+4x^{2}\)
- \(y=3x^{2}−4x−2\)
- \(y=6x^{2}−8x+5\)
- Відповідь
-
1. Максимум:\(y = 10\)
3. Мінімум:\(y = 4\)
5. Максимум:\(y = 0\)
7. Максимум:\(y = 10\)
9. Мінімум:\(y = −\frac{10}{3}\)
Вправа\(\PageIndex{9}\) maximum or minimum
З огляду на наступні квадратичні функції, визначають область і діапазон.
- \(f(x)=3x^{2}+30x+50\)
- \(f(x)=5x^{2}−10x+1\)
- \(g(x)=−2x^{2}+4x+1\)
- \(g(x)=−7x^{2}−14x−9\)
- Висота в ногах, досягнута бейсболом, кинутим вгору зі швидкістю 48 футів/секунду від землі, задається функцією\(h(t)=−16t^{2}+48t\), де t представляє час у секундах. Що таке бейсбол 's максимальна висота і скільки часу буде потрібно, щоб досягти цієї висоти?
- Висота снаряда, запущеного прямо з кургану, задається функцією\(h(t)=−16t^{2}+96t+4\), де t представляє секунди після запуску. Яка максимальна висота?
- Прибуток у доларах, одержуваний виробництвом та продажем x нестандартних ламп, надається функцією\(P(x)=−10x^{2}+800x−12,000\). Яка максимальна прибуток?
- Дохід у доларах, отриманий від продажу певного товару, моделюється за формулою\(R(x)=100x−0.0025x^{2}\), де x представляє кількість проданих одиниць. Яку кількість одиниць потрібно продати, щоб максимізувати дохід?
- Середня кількість звернень до веб-сайту радіостанції моделюється за формулою\(f(x)=450t^{2}−3,600t+8,000\), де t представляє кількість годин з 8:00 ранку, в яку годину дня кількість звернень до веб-сайту мінімально?
- Значення в доларах нового автомобіля моделюється за формулою\(V(t)=125t^{2}−3,000t+22,000\), де t представляє кількість років з моменту його придбання. Визначте мінімальне значення автомобіля.
- Щоденні виробничі витрати в доларах текстильної компанії, що виробляє спеціальну уніформу, моделюються за формулою\(C(x)=0.02x^{2}−20x+10,000\), де х представляє кількість виробленої уніформи.
- Скільки уніформи слід виготовити, щоб мінімізувати щоденні витрати на виробництво?
- Яка мінімальна добова собівартість виробництва?
- Площа певного прямокутного пера задається формулою\(A=14w−w^{2}\), де w представляє ширину в футах. Визначте ширину, яка виробляє максимальну площу.
- Відповідь
-
1. Домен: R; діапазон:\([−25,∞)\)
3. Домен: R; діапазон:\((−∞,3]\)
5. Максимальна висота 36 футів настає через 1,5 секунди.
7. 4000 доларів
9. 12:00
11. a. 500 уніформа; б. $5,000
Вправа\(\PageIndex{10}\) vertex by completing the square
Визначаємо вершину.
- \(y=−(x−5)^{2}+3\)
- \(y=−2(x−1)^{2}+7\)
- \(y=5(x+1)^{2}+6\)
- \(y=3(x+4)^{2}+10\)
- \(y=−5(x+8)^{2}−1\)
- \(y=(x+2)^{2}−5\)
- Відповідь
-
1. \((5, 3)\)
3. \((-1, 6)\)
5. \((-8, -1)\)
Вправа\(\PageIndex{11}\) vertex by completing the square
Перепишіть за\(y=a(x−h)^{2}+k\) формою і визначте вершину.
- \(y=x^{2}−14x+24\)
- \(y=x^{2}−12x+40\)
- \(y=x^{2}+4x−12\)
- \(y=x^{2}+6x−1\)
- \(y=2x^{2}−12x−3\)
- \(y=3x^{2}−6x+5\)
- \(y=−x^{2}+16x+17\)
- \(y=−x^{2}+10x\)
- Відповідь
-
1. \(y=(x−7)^{2}−25\); вершина:\((7, −25)\)
3. \(y=(x+2)^{2}−16\); вершина:\((−2, −16)\)
5. \(y=2(x−3)^{2}−21\); вершина:\((3, −21)\)
7. \(y=−(x−8)^{2}+81\); вершина:\((8, 81)\)
Вправа\(\PageIndex{12}\) vertex by completing the square
Графік.
- \(y=x^{2}−1\)
- \(y=x^{2}+1\)
- \(y=(x−1)^{2}\)
- \(y=(x+1)^{2}\)
- \(y=(x−4)^{2}−9\)
- \(y=(x−1)^{2}−4\)
- \(y=−2(x+1)^{2}+8\)
- \(y=−3(x+2)^{2}+12\)
- \(y=−5(x−1)^{2}\)
- \(y=−(x+2)^{2}\)
- \(y=−4(x−1)^{2}−2\)
- \(y=9(x+1)^{2}+2\)
- \(y=(x+5)^{2}−15\)
- \(y=2(x−5)^{2}−3\)
- \(y=−2(x−4)^{2}+22\)
- \(y=2(x+3)^{2}−13\)
- Відповідь
-
1.
.png)
Малюнок\(\PageIndex{32}\) 3.
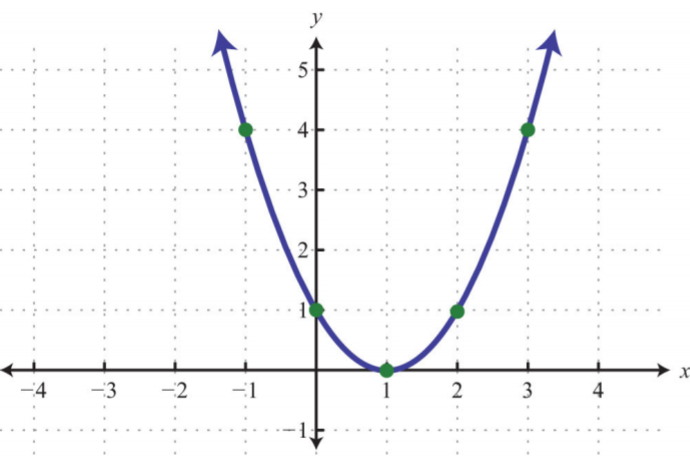.png)
Малюнок\(\PageIndex{33}\) 5.
.png)
Малюнок\(\PageIndex{34}\) 7.
.png)
Малюнок\(\PageIndex{35}\) 9.
.png)
Малюнок\(\PageIndex{36}\) 11.
.png)
Малюнок\(\PageIndex{37}\) 13.
.png)
Малюнок\(\PageIndex{38}\) 15.
.png)
Малюнок\(\PageIndex{39}\)
Вправа\(\PageIndex{13}\) discussion board
- Запишіть свій план складання параболи на іспиті. Що ви будете шукати і як ви представите свою відповідь? Поділіться своїм планом на дошці обговорень.
- Чому будь-яка парабола, яка відкривається вгору або вниз, є функцією? Поясніть однокласнику, як визначити домен і діапазон.
- Відповідь
-
1. Відповіді можуть відрізнятися
