12.2: Гіпербола

Цілі навчання

• Знайдіть вершини та вогнища гіперболи.
• Напишіть рівняння гіпербол в стандартній формі.
• Гіперболи графа з центром у початковій точці.
• Гіперболи графа не зосереджені на початку.
• Вирішити прикладні проблеми, пов'язані з гіперболами.

Що спільного мають шляхи комет, надзвукових стріл, давньогрецьких стовпів та градирень з природною тягою? Всі вони можуть бути змодельовані одним і тим же типом конічних. Наприклад, коли щось рухається швидше швидкості звуку, створюється ударна хвиля у вигляді конуса. Частина конуса утворюється, коли хвиля перетинає землю, в результаті чого утворюється звукова стріла (рис.\(\PageIndex{1}\)).

Малюнок\(\PageIndex{1}\): Ударна хвиля, що перетинає землю, утворює частину конічного конуса і призводить до звукової стріли.

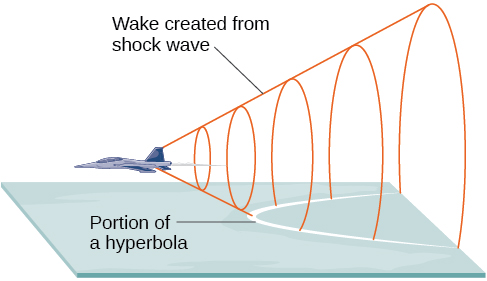
Більшість людей знайомі з звуковим бумом, створеним надзвуковими літаками, але люди порушували звуковий бар'єр задовго до першого надзвукового польоту. Тріск батіга виникає через те, що кінчик перевищує швидкість звуку. Кулі, зняті з багатьох вогнепальної зброї, також порушують звуковий бар'єр, хоча удар гармати зазвичай витісняє звук звукового буму.

Розташування вершин і вогнищ гіперболи

В аналітичній геометрії гіпербола - це конічний переріз, утворений перетином прямого кругового конуса площиною під кутом таким, що обидві половини конуса перетинаються. Це перетин створює дві окремі необмежені криві, які є дзеркальним відображенням один одного (рис.\(\PageIndex{2}\)).

Малюнок\(\PageIndex{2}\): Гіпербола

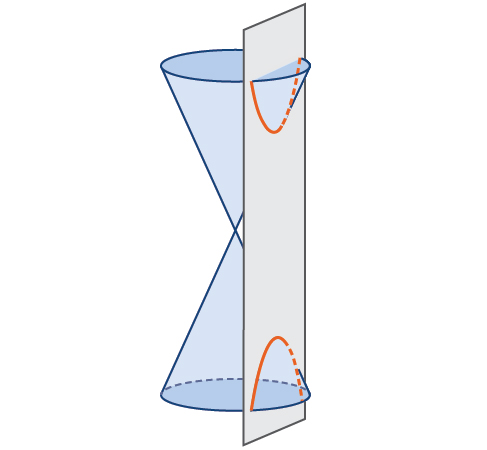
Як і еліпс, гіперболу також можна визначити як набір точок у координатній площині. Гіпербола - це сукупність всіх точок на\((x,y)\) площині таким чином, що різниця відстаней між\((x,y)\) і вогнищами є позитивною константою.

Зверніть увагу, що визначення гіперболи дуже схоже на визначення еліпса. Відмінність полягає в тому, що гіпербола визначається через різницю двох відстаней, тоді як еліпс визначається через суму двох відстаней.

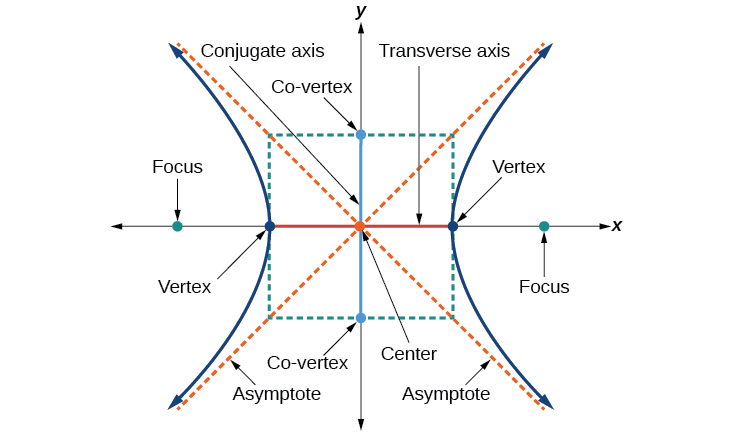
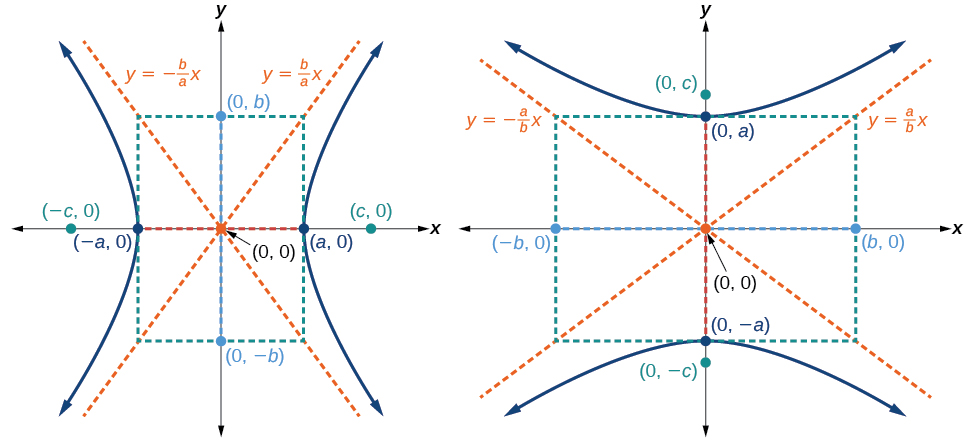
Як і у випадку з еліпсом, кожна гіпербола має дві осі симетрії. Поперечна вісь - це відрізок лінії, який проходить через центр гіперболи і має вершини в якості своїх кінцевих точок. Вогнища лежать на лінії, яка містить поперечну вісь. Спряжена вісь перпендикулярна поперечній осі і має співвершини як свої кінцеві точки. Центр гіперболи - це середина як поперечної, так і сполученої осей, де вони перетинаються. Кожна гіпербола також має два асимптоти, які проходять через її центр. Оскільки гіпербола відступає від центру, її гілки наближаються до цих асимптотів. Центральний прямокутник гіперболи зосереджений на початку координат зі сторонами, які проходять через кожну вершину та співвершину; це корисний інструмент для побудови графіків гіперболи та її асимптотів. Щоб намалювати асимптоти гіперболи, просто накидайте і подовжте діагоналі центрального прямокутника (рис.\(\PageIndex{3}\)).

Малюнок\(\PageIndex{3}\): Основні особливості гіперболи

У цьому розділі ми обмежимо наше обговорення гіперболами, які розташовані вертикально або горизонтально в координатній площині; осі будуть лежати або паралельні\(y\) осям\(x\) - і -. Ми розглянемо два випадки: ті, які зосереджені на початку, і ті, які зосереджені в точці, відмінній від походження.

Виведення рівняння еліпса з центром на початку

\((−c,0)\)\((c,0)\)Дозволяти і бути вогнища гіперболи, зосереджені на початку. Гіпербола - це сукупність всіх точок\((x,y)\) такого, що різниця відстаней від\((x,y)\) до вогнищ постійна. Див\(\PageIndex{4}\). Малюнок.

Малюнок\(\PageIndex{4}\)

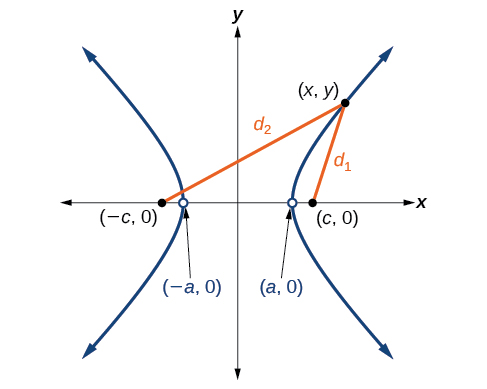
Якщо\((a,0)\) є вершиною гіперболи, відстань від\((−c,0)\) до\((a,0)\) дорівнює\(a−(−c)=a+c\). Відстань від\((c,0)\) до\((a,0)\) є\(c−a\). Сума відстаней від вогнищ до вершини дорівнює

\((a+c)−(c−a)=2a\)

Якщо\((x,y)\) це точка на гіперболі, ми можемо визначити наступні змінні:

\(d_2=\)відстань від\((−c,0)\) до\((x,y)\)

\(d_1=\)відстань від\((c,0)\) до\((x,y)\)

За визначенням гіперболи,\(d_2−d_1\) є постійною для будь-якої точки\((x,y)\) на гіперболі. Ми знаємо, що різниця цих відстаней -\(2a\) для вершини\((a,0)\). Звідси випливає, що\(d_2−d_1=2a\) для будь-якої точки на гіперболі. Як і при виведенні рівняння еліпса, почнемо з застосування формули відстані. Решта деривація - алгебраїчна. Порівняйте цей похідний з попереднім розділом для еліпсів.

\[\begin{align*} d_2-d_1&=2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}-\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance Formula}\\ \sqrt{{(x+c)}^2+y^2}-\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a+\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={(2a+\sqrt{{(x-c)}^2+y^2})}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining square.}\\ 2cx&=4a^2+4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {(cx-a^2)}^2&=a^2{\left[\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^4+c^2x^2&=a^2x^2+a^2c^2+a^2y^2\qquad \text{Combine like terms.}\\ c^2x^2-a^2x^2-a^2y^2&=a^2c^2-a^4\qquad \text{Rearrange terms.}\\ x^2(c^2-a^2)-a^2y^2&=a^2(c^2-a^2)\qquad \text{Factor common terms.}\\ x^2b^2-a^2y^2&=a^2b^2\qquad \text{Set } b^2=c^2−a^2\\. \dfrac{x^2b^2}{a^2b^2}-\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\\ \end{align*}\]

Це рівняння визначає гіперболу з центром у початку з вершинами\((\pm a,0)\) та співвершинами\((0,\pm b)\).

СТАНДАРТНІ ФОРМИ РІВНЯННЯ ГІПЕРБОЛИ З ЦЕНТРОМ\((0,0)\)

Стандартна форма рівняння гіперболи з центром\((0,0)\) і поперечною віссю на\(x\) -осі дорівнює

\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)

де

• довжина поперечної осі дорівнює\(2a\)
• координати вершин\((\pm a,0)\)
• довжина сполученої осі дорівнює\(2b\)
• координати співвершин\((0,\pm b)\)
• відстань між вогнищами становить\(2c\), де\(c^2=a^2+b^2\)
• координати вогнищ\((\pm c,0)\)
• рівняння асимптотів\(y=\pm \dfrac{b}{a}x\)

Див\(\PageIndex{5a}\). Малюнок.

Стандартна форма рівняння гіперболи з центром\((0,0)\) і поперечною віссю на\(y\) -осі дорівнює

\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)

де

• довжина поперечної осі дорівнює\(2a\)
• координати вершин\((0,\pm a)\)
• довжина сполученої осі дорівнює\(2b\)
• координати співвершин\((\pm b,0)\)
• відстань між вогнищами становить\(2c\), де\(c^2=a^2+b^2\)
• координати вогнищ\((0,\pm c)\)
• рівняння асимптотів\(y=\pm \dfrac{a}{b}x\)

Див\(\PageIndex{5b}\). Малюнок.

Зверніть увагу, що вершини, співвершини та вогнища пов'язані рівнянням\(c^2=a^2+b^2\). Коли нам дано рівняння гіперболи, ми можемо використовувати це співвідношення для ідентифікації її вершин і вогнищ.

Рисунок\(\PageIndex{5}\): (а) Горизонтальна гіпербола з центром\((0,0)\) (b) Вертикальна гіпербола з центром\((0,0)\)

Як: З огляду на рівняння гіперболи в стандартній формі, знайдіть її вершини та вогнища

1. Визначте, чи лежить поперечна вісь на\(x\) - або\(y\) -осі. Зверніть увагу, що завжди\(a^2\) знаходиться під змінною з позитивним коефіцієнтом. Отже, якщо встановити іншу змінну рівну нулю, ви легко зможете знайти перехоплення. У разі, коли гіпербола зосереджена у початку, перехоплення збігаються з вершинами.
   • Якщо рівняння має вигляд\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), то поперечна вісь лежить на\(x\) -осі. Вершини розташовуються в\((\pm a,0)\), а вогнища - на\((\pm c,0)\).
   • Якщо рівняння має вигляд\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), то поперечна вісь лежить на\(y\) -осі. Вершини розташовуються в\((0,\pm a)\), а вогнища - на\((0,\pm c)\).
2. Вирішіть для\(a\) використання рівняння\(a=\sqrt{a^2}\).
3. Вирішіть для\(c\) використання рівняння\(c=\sqrt{a^2+b^2}\).

Приклад\(\PageIndex{1}\): Locating a Hyperbola’s Vertices and Foci

Визначте вершини і вогнища гіперболи за допомогою рівняння\(\dfrac{y^2}{49}−\dfrac{x^2}{32}=1\).

Рішення

Рівняння має вигляд\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), тому поперечна вісь лежить на\(y\) -осі. Гіпербола зосереджена на початку, тому вершини служать y -перехопленнями графа. Щоб знайти вершини, встановити\(x=0\), і вирішити для\(y\).

\[\begin{align*} 1&=\dfrac{y^2}{49}-\dfrac{x^2}{32}\\ 1&=\dfrac{y^2}{49}-\dfrac{0^2}{32}\\ 1&=\dfrac{y^2}{49}\\ y^2&=49\\ y&=\pm \sqrt{49}\\ &=\pm 7 \end{align*}\]

Вогнища розташовуються при\((0,\pm c)\). Рішення для\(c\),

\[\begin{align*} c&=\sqrt{a^2+b^2}\\ &=\sqrt{49+32}\\ &=\sqrt{81}\\ &=9 \end{align*}\]

Тому вершини розташовуються при\((0,\pm 7)\), а вогнища розташовуються при\((0,9)\).

Вправа\(\PageIndex{1}\)

Визначте вершини і вогнища гіперболи за допомогою рівняння\(\dfrac{x^2}{9}−\dfrac{y^2}{25}=1\).

Відповідь

Вершини:\((\pm 3,0)\); Вогнища:\((\pm \sqrt{34},0)\)

Написання рівнянь гіпербол у стандартній формі

Так само, як і у випадку з еліпсами, написання рівняння для гіперболи в стандартній формі дозволяє обчислити ключові особливості: її центр, вершини, співвершини, вогнища, асимптоти, а також довжини та положення поперечних і сполучених осей. І навпаки, рівняння для гіперболи можна знайти з огляду на її ключові особливості. Почнемо з пошуку стандартних рівнянь для гіпербол, орієнтованих на початок. Тоді ми звернемо увагу на пошук стандартних рівнянь для гіпербол, розташованих по центру в якійсь точці, відмінній від початку.

Гіперболи в центрі походження

Розглядаючи стандартні форми, наведені для гіпербол з центром\((0,0)\), ми бачимо, що вершини, співвершини та вогнища пов'язані рівнянням\(c^2=a^2+b^2\). Зверніть увагу, що це рівняння також можна переписати як\(b^2=c^2−a^2\). Ця залежність використовується для запису рівняння для гіперболи, коли задані координати її вогнищ і вершин.

Як: З огляду на вершини та вогнища гіперболи з центром\((0,0)\), write its equation in standard form

1. Визначте, чи лежить поперечна вісь на\(x\) - або\(y\) -осі.
   • Якщо задані координати вершин і вогнищ мають вигляд\((\pm a,0)\) і\((\pm c,0)\), відповідно, то поперечна вісь є\(x\) -віссю. Використовуйте стандартну форму\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).
   • Якщо задані координати вершин і вогнищ мають вигляд\((0,\pm a)\) і\((0,\pm c)\), відповідно, то поперечна вісь є\(y\) -віссю. Використовуйте стандартну форму\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\).
2. Знайти\(b^2\) за допомогою рівняння\(b^2=c^2−a^2\).
3. Підставити значення для\(a^2\) і\(b^2\) в стандартну форму рівняння, визначеного в кроці 1.

Приклад\(\PageIndex{2}\): Finding the Equation of a Hyperbola Centered at \((0,0)\) Given its Foci and Vertices

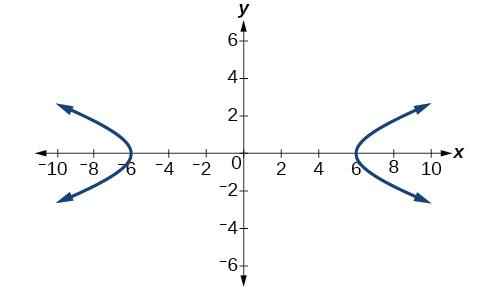
Що таке стандартне рівняння форми гіперболи, що має вершини\((\pm 6,0)\) і вогнища\((\pm 2\sqrt{10},0)\)?

Рішення

Вершини і вогнища знаходяться на\(x\) -осі. Таким чином, рівняння для гіперболи матиме вигляд\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).

Вершини є\((\pm 6,0)\), так\(a=6\) і\(a^2=36\).

Вогнища є\((\pm 2\sqrt{10},0)\), так\(c=2\sqrt{10}\) і\(c^2=40\).

Рішення для\(b^2\), у нас є

\[\begin{align*} b^2&=c^2-a^2\\ b^2&=40-36\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=4\qquad \text{Subtract.} \end{align*}\]

Нарешті, підставляємо\(a^2=36\) і\(b^2=4\) в стандартну форму рівняння,\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\). Рівняння гіперболи є\(\dfrac{x^2}{36}−\dfrac{y^2}{4}=1\), як показано на малюнку\(\PageIndex{6}\).

Малюнок\(\PageIndex{6}\)

Вправа\(\PageIndex{2}\)

Що таке стандартне рівняння форми гіперболи, що має вершини\((0,\pm 2)\) і вогнища\((0,\pm 2\sqrt{5})\)?

Відповідь

\(\dfrac{y^2}{4}−\dfrac{x^2}{16}=1\)

Гіперболи не в центрі походження

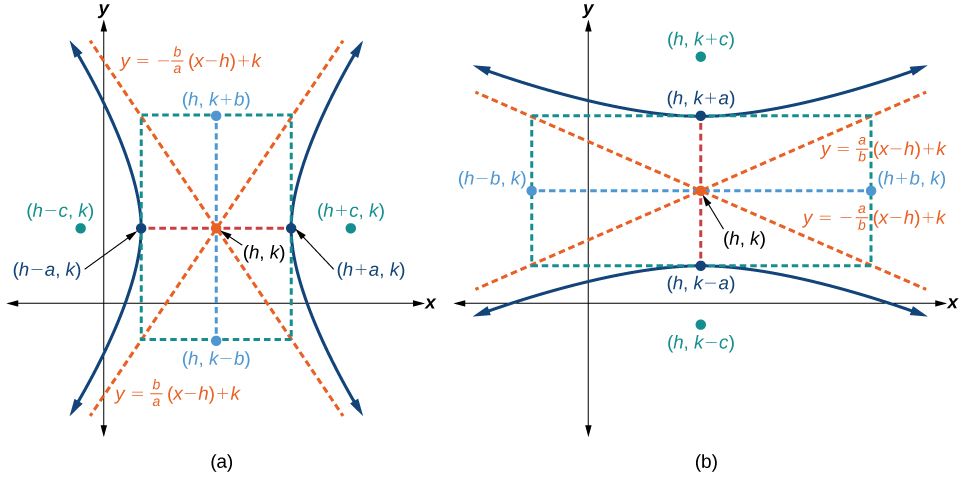
Як і графіки для інших рівнянь, графік гіперболи можна перекласти. Якщо гіпербола перекладається\(h\) одиницями горизонтально, а\(k\) одиниці вертикально, центр гіперболи буде\((h,k)\). Цей переклад призводить до стандартної форми рівняння, яке ми бачили раніше,\(x\) замінене\((x−h)\) і\(y\) замінене на\((y−k)\).

СТАНДАРТНІ ФОРМИ РІВНЯННЯ ГІПЕРБОЛИ З ЦЕНТРОМ\((H, K)\)

Стандартна форма рівняння гіперболи з центром\((h,k)\) і поперечною віссю паралельно\(x\) -осі дорівнює

\[\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\]

де

• довжина поперечної осі дорівнює\(2a\)
• координати вершин\((h\pm a,k)\)
• довжина сполученої осі дорівнює\(2b\)
• координати співвершин\((h,k\pm b)\)
• відстань між вогнищами становить\(2c\), де\(c^2=a^2+b^2\)
• координати вогнищ\((h\pm c,k)\)

Асимптоти гіперболи збігаються з діагоналями центрального прямокутника. Довжина прямокутника дорівнює\(2a\) і його ширина дорівнює\(2b\). Нахили діагоналей є\(\pm \dfrac{b}{a}\), і кожна діагональ проходить через центр\((h,k)\). Використовуючи формулу точка-нахил, нескладно показати, що рівняння асимптотів є\(y=\pm \dfrac{b}{a}(x−h)+k\). Див\(\PageIndex{7a}\). Малюнок.

Стандартна форма рівняння гіперболи з центром\((h,k)\) і поперечною віссю паралельно\(y\) -осі дорівнює

\[\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\]

де

• довжина поперечної осі дорівнює\(2a\)
• координати вершин\((h,k\pm a)\)
• довжина сполученої осі дорівнює\(2b\)
• координати співвершин\((h\pm b,k)\)
• відстань між вогнищами становить\(2c\), де\(c^2=a^2+b^2\)
• координати вогнищ\((h,k\pm c)\)

Використовуючи міркування вище, рівняння асимптотів є\(y=\pm \dfrac{a}{b}(x−h)+k\). Див\(\PageIndex{7b}\). Малюнок.

Рисунок\(\PageIndex{7}\): (а) Горизонтальна гіпербола з центром\((h,k)\) (b) Вертикальна гіпербола з центром\((h,k)\)

Як і гіперболи, зосереджені на початку, гіперболи, зосереджені в точці,\((h,k)\) мають вершини, співвершини та вогнища, які пов'язані рівнянням\(c^2=a^2+b^2\). Ми можемо використовувати цей зв'язок разом із формулами середньої та відстані, щоб знайти стандартне рівняння гіперболи, коли задані вершини та вогнища.

Як: З огляду на вершини та вогнища гіперболи з центром\((h,k)\),write its equation in standard form

1. Визначте, чи паралельна поперечна вісь\(x\) - або\(y\) -осі.
   • Якщо\(y\) -координати заданих вершин і вогнищ однакові, то поперечна вісь паралельна\(x\) -осі. Використовуйте стандартну форму\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\).
   • Якщо\(x\) -координати заданих вершин і вогнищ однакові, то поперечна вісь паралельна\(y\) -осі. Використовуйте стандартну форму\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\).
2. Визначте центр гіперболи\((h,k)\), використовуючи формулу середньої точки та задані координати для вершин.
3. Знайти\(a^2\) шляхом вирішення для довжини поперечної осі\(2a\), яка є відстанню між заданими вершинами.
4. Знайдіть\(c^2\) використання\(h\) та\(k\) знайдене в кроці 2 разом із заданими координатами для вогнищ.
5. Вирішіть для\(b^2\) використання рівняння\(b^2=c^2−a^2\).
6. Підставте значення для\(h\),\(k\),\(a^2\), і\(b^2\) в стандартну форму рівняння, визначеного в кроці 1.

Приклад\(\PageIndex{3}\): Finding the Equation of a Hyperbola Centered at \((h, k)\) Given its Foci and Vertices

Що таке стандартне рівняння форми гіперболи, що має вершини в\((0,−2)\) і\((6,−2)\) і вогнища при\((−2,−2)\) і\((8,−2)\)?

Рішення

\(y\)-координати вершин і вогнищ однакові, тому поперечна вісь паралельна\(x\) -осі. Таким чином, рівняння гіперболи матиме вигляд

\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)

Спочатку визначаємо центр,\((h,k)\). Центр знаходиться на півдорозі між вершинами\((0,−2)\) і\((6,−2)\). Застосовуючи формулу середньої точки, ми маємо

\((h,k)=(\dfrac{0+6}{2},\dfrac{−2+(−2)}{2})=(3,−2)\)

Далі знаходимо\(a^2\). Довжина поперечної осі\(2a\),, обмежена вершинами. Отже, ми можемо знайти,\(a^2\) знайшовши відстань між\(x\) -координатами вершин.

\[\begin{align*} 2a&=| 0-6 |\\ 2a&=6\\ a&=3\\ a^2&=9 \end{align*}\]

Тепер нам потрібно знайти\(c^2\). Координати вогнищ є\((h\pm c,k)\). Так\((h−c,k)=(−2,−2)\) і\((h+c,k)=(8,−2)\). Ми можемо використовувати\(x\) -coordinate з будь-якої з цих точок для вирішення\(c\). Використовуючи точку\((8,−2)\), і підставляючи\(h=3\),

\[\begin{align*} h+c&=8\\ 3+c&=8\\ c&=5\\ c^2&=25 \end{align*}\]

Далі вирішуємо за\(b^2\) допомогою рівняння\(b^2=c^2−a^2\):

\[\begin{align*} b^2&=c^2-a^2\\ &=25-9\\ &=16 \end{align*}\]

Нарешті, підставити значення, знайдені для\(h\)\(k\),\(a^2\), і\(b^2\) в стандартну форму рівняння.

\(\dfrac{{(x−3)}^2}{9}−\dfrac{{(y+2)}^2}{16}=1\)

Вправа\(\PageIndex{3}\)

Що таке стандартне рівняння форми гіперболи, що має вершини\((1,−2)\) і\((1,8)\) і вогнища\((1,−10)\) і\((1,16)\)?

Відповідь

\(\dfrac{{(y−3)}^2}{25}+\dfrac{{(x−1)}^2}{144}=1\)

Графічні гіперболи, орієнтовані на початок

Коли ми маємо рівняння у стандартній формі для гіперболи, зосередженої на початку, ми можемо інтерпретувати його частини, щоб визначити ключові особливості його графа: центр, вершини, співвершини, асимптоти, вогнища та довжини та положення поперечних та сполучених осей. Для побудови графіків гіпербол, орієнтованих на початок, ми використовуємо стандартну форму\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\) для горизонтальних гіпербол і стандартну форму\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\) для вертикальних гіпербол.

Як: Задано стандартне рівняння форми для гіперболи з центром\((0,0)\), sketch the graph

1. Визначте, яка з стандартних форм застосовується до даного рівняння.
2. Використовуйте стандартну форму, визначену на кроці 1, для визначення положення поперечної осі; координати для вершин, співвершин та вогнищ; і рівняння для асимптотів.
   • Якщо рівняння у вигляді\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), то
     • поперечна вісь знаходиться на\(x\) -осі
     • координати вершин\ ((\ pm a,0)\ 0
     • координати співвершин\((0,\pm b)\)
     • координати вогнищ\((\pm c,0)\)
     • рівняння асимптотів\(y=\pm \dfrac{b}{a}x\)
   • Якщо рівняння у вигляді\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), то
     • поперечна вісь знаходиться на\(y\) -осі
     • координати вершин\((0,\pm a)\)
     • координати співвершин\((\pm b,0)\)
     • координати вогнищ\((0,\pm c)\)
     • рівняння асимптотів\(y=\pm \dfrac{a}{b}x\)
3. Вирішіть для координат вогнищ за допомогою рівняння\(c=\pm \sqrt{a^2+b^2}\).
4. Покладіть вершини, співвершини, вогнища та асимптоти в координатній площині та намалюйте гладку криву, щоб сформувати гіперболу.

Приклад\(\PageIndex{4}\): Graphing a Hyperbola Centered at \((0,0)\) Given an Equation in Standard Form

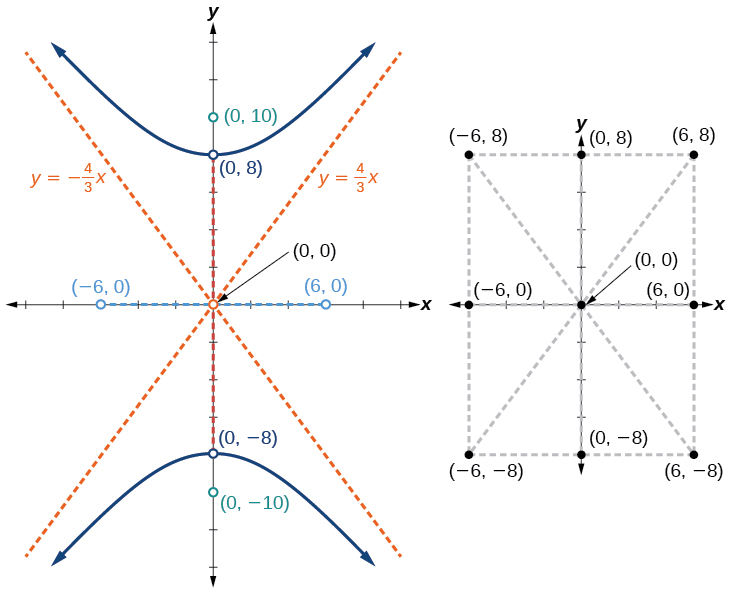
Графік гіперболи, заданої рівнянням\(\dfrac{y^2}{64}−\dfrac{x^2}{36}=1\). Визначте та позначте вершини, співвершини, вогнища та асимптоти.

Рішення

Стандартна форма, яка застосовується до даного рівняння, є\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\). Таким чином, поперечна вісь знаходиться на\(y\) -осі

Координати вершин\((0,\pm a)=(0,\pm \sqrt{64})=(0,\pm 8)\)

Координати співвершин\((\pm b,0)=(\pm \sqrt{36}, 0)=(\pm 6,0)\)

Координати вогнищ - це\((0,\pm c)\), де\(c=\pm \sqrt{a^2+b^2}\). Рішення для\(c\), у нас є

\(c=\pm \sqrt{a^2+b^2}=\pm \sqrt{64+36}=\pm \sqrt{100}=\pm 10\)

Тому координати вогнищ є\((0,\pm 10)\)

Рівняння асимптотів\(y=\pm \dfrac{a}{b}x=\pm \dfrac{8}{6}x=\pm \dfrac{4}{3}x\)

Покладіть та позначте вершини та співвершини, а потім намалюйте центральний прямокутник. Сторони прямокутника паралельні осям і проходять через вершини і співвершини. Намалюйте та розтягніть діагоналі центрального прямокутника, щоб показати асимптоти. Центральний прямокутник і асимптоти забезпечують основу, необхідну для створення точного графіка гіперболи. Позначте вогнища і асимптоти і намалюйте плавну криву, щоб сформувати гіперболу, як показано на малюнку\(\PageIndex{8}\).

Малюнок\(\PageIndex{8}\)

Вправа\(\PageIndex{4}\)

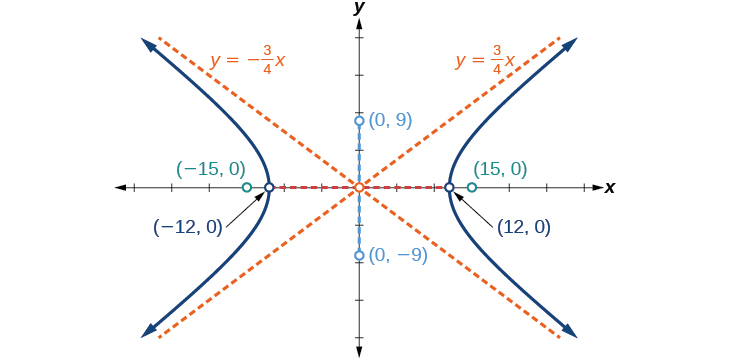
Графік гіперболи, заданої рівнянням\(\dfrac{x^2}{144}−\dfrac{y^2}{81}=1\). Визначте та позначте вершини, співвершини, вогнища та асимптоти.

Відповідь

вершини:\((\pm 12,0)\); ко-вершини:\((0,\pm 9)\); осередки:\((\pm 15,0)\); асимптоти:\(y=\pm \dfrac{3}{4}x\);

Малюнок\(\PageIndex{9}\)

Графічні гіперболи, які не зосереджені на початку

Графічне зображення гіпербол з центром у точці,\((h,k)\) відмінній від початку, схоже на графічні еліпси з центром у точці, відмінній від початку. Використовуємо стандартні форми як\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\) для горизонтальних гіпербол, так і\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\) для вертикальних гіпербол. З цих рівнянь стандартної форми ми можемо легко обчислити та побудувати ключові особливості графа: координати його центру, вершин, співвершин та вогнищ; рівняння його асимптотів; та положення поперечних та сполучених осей.

Як: Задано загальну форму для гіперболи, зосередженої на\((h, k)\), sketch the graph

1. Перетворіть загальну форму на цю стандартну форму. Визначте, яка з стандартних форм застосовується до даного рівняння.
2. Використовуйте стандартну форму, визначену на кроці 1, для визначення положення поперечної осі; координати центру, вершин, співвершин, вогнищ; і рівнянь для асимптотів.
   1. Якщо рівняння у вигляді\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), то
      • поперечна вісь паралельна\(x\) -осі
      • центр - це\((h,k)\)
      • координати вершин\((h\pm a,k)\)
      • координати співвершин\((h,k\pm b)\)
      • координати вогнищ\((h\pm c,k)\)
      • рівняння асимптотів\(y=\pm \dfrac{b}{a}(x−h)+k\)
   2. Якщо рівняння у вигляді\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\), то
      • поперечна вісь паралельна\(y\) -осі
      • центр - це\((h,k)\)
      • координати вершин\((h,k\pm a)\)
      • координати співвершин\((h\pm b,k)\)
      • координати вогнищ\((h,k\pm c)\)
      • рівняння асимптотів\(y=\pm \dfrac{a}{b}(x−h)+k\)
3. Вирішіть для координат вогнищ за допомогою рівняння\(c=\pm \sqrt{a^2+b^2}\).
4. Покладіть центр, вершини, співвершини, вогнища та асимптоти в координатній площині та намалюйте плавну криву, щоб сформувати гіперболу.

Приклад\(\PageIndex{5}\): Graphing a Hyperbola Centered at \((h, k)\) Given an Equation in General Form

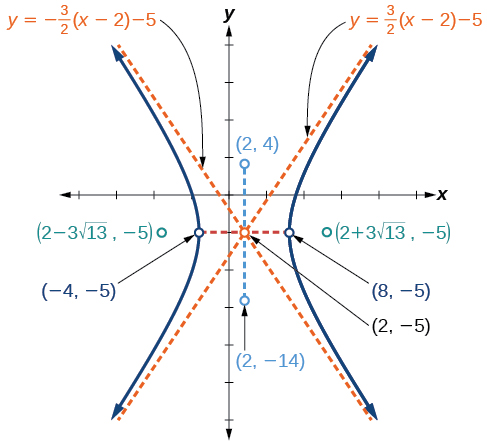
Графік гіперболи, заданої рівнянням\(9x^2−4y^2−36x−40y−388=0\). Визначте та позначте центр, вершини, співвершини, вогнища та асимптоти.

Рішення

Почніть з вираження рівняння в стандартній формі. Групуйте члени, які містять одну і ту ж змінну, і перемістіть константу в протилежну сторону рівняння.

\((9x^2−36x)−(4y^2+40y)=388\)

Коефіцієнт провідного коефіцієнта кожного виразу.

\(9(x^2−4x)−4(y^2+10y)=388\)

Завершіть квадрат двічі. Не забудьте збалансувати рівняння, додаючи однакові константи до кожної сторони.

\(9(x^2−4x+4)−4(y^2+10y+25)=388+36−100\)

Перепишіть як ідеальні квадрати.

\(9{(x−2)}^2−4{(y+5)}^2=324\)

Розділіть обидві сторони на постійний член, щоб розмістити рівняння в стандартній формі.

\(\dfrac{{(x−2)}^2}{36}−\dfrac{{(y+5)}^2}{81}=1\)

Стандартна форма, яка застосовується до даного рівняння - це\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), де\(a^2=36\) і\(b^2=81\), або\(a=6\) і\(b=9\). Таким чином, поперечна вісь паралельна\(x\) -осі. Звідси випливає, що:

центр еліпса\((h,k)=(2,−5)\)

координати вершин є\((h\pm a,k)=(2\pm 6,−5)\), або\((−4,−5)\) і\((8,−5)\)

координати співвершин є\((h,k\pm b)=(2,−5\pm 9)\), або\((2,−14)\) і\((2,4)\)

координати вогнищ знаходяться\((h\pm c,k)\), де\(c=\pm \sqrt{a^2+b^2}\). Рішення для\(c\), у нас є

\(c=\pm \sqrt{36+81}=\pm \sqrt{117}=\pm 3\sqrt{13}\)

Тому координати вогнищ -\((2−3\sqrt{13},−5)\) і\((2+3\sqrt{13},−5)\).

Рівняння асимптотів є\(y=\pm \dfrac{b}{a}(x−h)+k=\pm \dfrac{3}{2}(x−2)−5\).

Далі ми будуємо та позначимо центр, вершини, співвершини, вогнища та асимптоти та малюємо плавні криві, щоб сформувати гіперболу, як показано на малюнку\(\PageIndex{10}\).

Малюнок\(\PageIndex{10}\)

Вправа\(\PageIndex{5}\)

Графік гіперболи, заданої стандартною формою рівняння\(\dfrac{{(y+4)}^2}{100}−\dfrac{{(x−3)}^2}{64}=1\). Визначте та позначте центр, вершини, співвершини, вогнища та асимптоти.

Відповідь

центр:\((3,−4)\); вершини:\((3,−14)\) і\((3,6)\); ко-вершини:\((−5,−4)\); і\((11,−4)\); вогнища:\((3,−4−2\sqrt{41})\) і\((3,−4+2\sqrt{41})\); асимптоти:\(y=\pm \dfrac{5}{4}(x−3)−4\)

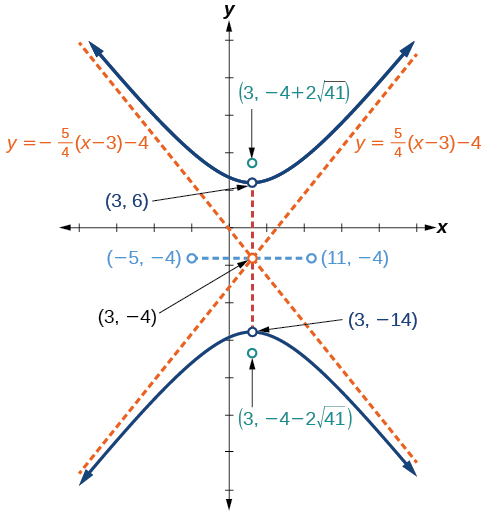
Малюнок\(\PageIndex{11}\)

Рішення прикладних проблем за участю гіперболи

Як ми обговорювали на початку цього розділу, гіперболи мають реальні застосування в багатьох галузях, таких як астрономія, фізика, техніка та архітектура. Ефективність конструкції гіперболічних градирень особливо цікава. Градирні використовуються для передачі відпрацьованого тепла в атмосферу і часто рекламуються за їх здатність ефективно генерувати енергію. Через свою гіперболічну форму ці конструкції здатні протистояти екстремальним вітрам, при цьому вимагають менше матеріалу, ніж будь-які інші форми своїх розмірів і міцності (рис.\(\PageIndex{12}\)). Наприклад, вежа\(500\) -футів може бути виготовлена лише із залізобетонної оболонки\(6\) або шириною в\(8\) дюйми!

Ілюстрація\(\PageIndex{12}\): Градирні на електростанції Drax в Північному Йоркширі, Великобританія (кредит: Les Haines, Flickr)

Перші гіперболічні вежі були спроектовані в 1914 році і мали\(35\) висоту метрів. Сьогодні найвищі градирні знаходяться у Франції, що стоять чудовими\(170\) метрами заввишки. У прикладі\(\PageIndex{6}\) ми будемо використовувати макет конструкції градирні, щоб знайти гіперболічне рівняння, яке моделює її сторони.

Приклад\(\PageIndex{6}\): Solving Applied Problems Involving Hyperbolas

Проектна схема градирні показана на малюнку\(\PageIndex{13}\). Вежа висотою\(179.6\) метрів. Діаметр верхівки -\(72\) метри. У найближчих до них сторони вежі знаходяться в\(60\) метрах один від одного.

Малюнок\(\PageIndex{13}\): Дизайн проекту для градирні з природною тягою

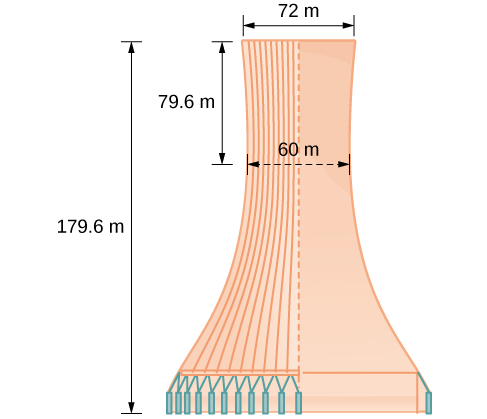
Знайдіть рівняння гіперболи, що моделює сторони градирні. Припустимо, що центр гіперболи, позначений перетином пунктирних перпендикулярних ліній на малюнку, є початком координатної площини. Округлення кінцевих значень до чотирьох знаків після коми.

Рішення

Ми припускаємо, що центр вежі знаходиться біля початку, тому ми можемо використовувати стандартну форму горизонтальної гіперболи, зосередженої на початку:\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), де гілки гіперболи утворюють сторони градирні. Ми повинні знайти значення\(a^2\) та\(b^2\) завершити модель.

Спочатку знаходимо\(a^2\). Нагадаємо, що довжина поперечної осі гіперболи дорівнює\(2a\). Ця довжина представлена відстанню, де сторони знаходяться найближче, яке дається як\(65.3\) метри. Отже,\(2a=60\). Тому\(a=30\) і\(a^2=900\).

Щоб вирішити для\(b^2\), нам потрібно підставити\(x\) і\(y\) в нашому рівнянні, використовуючи відому точку. Для цього ми можемо використовувати розміри вежі, щоб знайти якусь точку\((x,y)\), яка лежить на гіперболі. Ми будемо використовувати верхній правий кут вежі, щоб представити цю точку. Оскільки\(y\) -вісь перетинає вежу, наше\(x\) -значення може бути представлено радіусом вершини, або\(36\) метрами. Значення y представлено відстанню від початку до вершини, яке задається у вигляді\(79.6\) метрів. Тому,

\[\begin{align*} \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\qquad \text{Standard form of horizontal hyperbola.}\\ b^2&=\dfrac{y^2}{\dfrac{x^2}{a^2}-1}\qquad \text{Isolate } b^2\\ &=\dfrac{{(79.6)}^2}{\dfrac{{(36)}^2}{900}-1}\qquad \text{Substitute for } a^2,\: x, \text{ and } y\\ &\approx 14400.3636\qquad \text{Round to four decimal places} \end{align*}\]

Сторони вежі можуть бути змодельовані гіперболічним рівнянням

\(\dfrac{x^2}{900}−\dfrac{y^2}{14400.3636}=1\), або\(\dfrac{x^2}{{30}^2}−\dfrac{y^2}{{120.0015}^2}=1\)

Вправа\(\PageIndex{6}\)

Конструкція для проекту градирні показана на малюнку\(\PageIndex{14}\). Знайдіть рівняння гіперболи, що моделює сторони градирні. Припустимо, що центр гіперболи, позначений перетином пунктирних перпендикулярних ліній на малюнку, є початком координатної площини. Округлення кінцевих значень до чотирьох знаків після коми.

Малюнок\(\PageIndex{14}\)

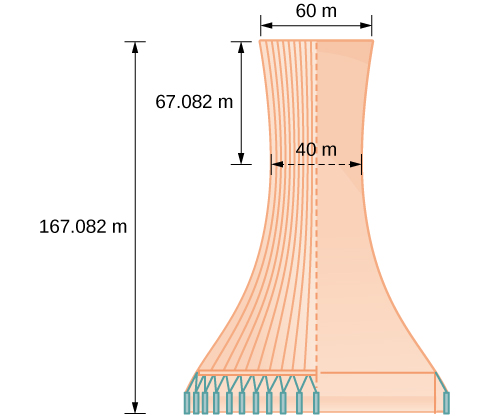
Відповідь

Сторони вежі можна змоделювати гіперболічним рівнянням. \(\dfrac{x^2}{400}−\dfrac{y^2}{3600}=1\)або\(\dfrac{x^2}{{20}^2}−\dfrac{y^2}{{60}^2}=1\).

Медіа

Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з гіперболами.

• Конічні перерізи: Гіпербола Частина 1 з 2
• Конічні перерізи: Гіпербола Частина 2 з 2
• Графік гіперболи з центром на початку
• Графік гіперболи з центром не на початку

Ключові рівняння

Гіпербола, центр у початку, поперечна вісь на осі x	\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)
Гіпербола, центр у початку, поперечна вісь на осі y	\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)
Гіпербола, центр в\((h,k)\), поперечна вісь паралельна осі х	\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)
Гіпербола, центр в\((h,k)\), поперечна вісь паралельна осі y	\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\)

Ключові поняття

• Гіпербола - це сукупність всіх точок на\((x,y)\) площині таким чином, що різниця відстаней між\((x,y)\) і вогнищами є позитивною константою.
• Стандартна форма гіперболи може використовуватися для розташування її вершин і вогнищ. Див\(\PageIndex{1}\). Приклад.
• Коли задані координати вогнищ і вершин гіперболи, ми можемо записати рівняння гіперболи в стандартному вигляді. Див. Приклад\(\PageIndex{2}\) і Приклад\(\PageIndex{3}\).
• Коли задано рівняння для гіперболи, ми можемо визначити її вершини, співвершини, вогнища, асимптоти, а також довжини та положення поперечних та сполучених осей для того, щоб графікувати гіперболу. Див. Приклад\(\PageIndex{4}\) і Приклад\(\PageIndex{5}\).
• Реальні ситуації можуть бути змодельовані за допомогою стандартних рівнянь гіпербол. Наприклад, враховуючи розміри градирні природної тяги, ми можемо знайти гіперболічне рівняння, яке моделює її сторони. Див\(\PageIndex{6}\). Приклад.