2.4: Комплексні числа

Цілі навчання

• Додавання і віднімання комплексних чисел.
• Множення і ділення комплексних чисел.
• Розв'язуйте квадратні рівняння з комплексними числами

Виявлений Бенуа Мандельбротом близько 1980 року, набір Мандельброта є одним з найбільш впізнаваних фрактальних зображень. Зображення побудовано на теорії самоподібності та операції ітерації. Збільшення масштабу фрактального зображення приносить багато сюрпризів, особливо при високому рівні повторення деталізації, який з'являється зі збільшенням. Рівняння, яке генерує це зображення, виявляється досить простим.

Малюнок$\PageIndex{1}$: Набір Мандельброта демонструє схожість, що найкраще показано в анімації.

Для того щоб краще зрозуміти його, нам необхідно ознайомитися з новим набором чисел. Майте на увазі, що вивчення математики безперервно спирається на себе. Негативні цілі числа, наприклад, заповнюють порожнечу, залишену безліччю натуральних чисел. Множина раціональних чисел, в свою чергу, заповнює порожнечу, залишену безліччю цілих чисел. Безліч дійсних чисел заповнює порожнечу, залишену безліччю раціональних чисел. Не дивно, що набір дійсних чисел також має порожнечі. У цьому розділі ми вивчимо набір чисел, який заповнює порожнечі в наборі дійсних чисел і дізнаємося, як працювати всередині нього.

Вираження квадратних коренів від'ємних чисел кратними$i$

Ми знаємо, як знайти квадратний корінь будь-якого позитивного дійсного числа. Аналогічним чином ми можемо знайти квадратний корінь будь-якого від'ємного числа. Різниця в тому, що корінь не справжній. Якщо значення в радиканді від'ємне, то корінь вважається уявним числом.$i$ Уявне число визначається як квадратний корінь$−1$.

$$\sqrt{-1}=i$$

Отже, використовуючи властивості радикалів,

$$i^2=(\sqrt{-1})^2=-1$$

Ми можемо записати квадратний корінь будь-якого негативного числа як кратне$i$. Розглянемо квадратний корінь з$−49$.

$$\begin{align*} \sqrt{-49}&= \sqrt{49\times(-1)}\\[4pt] &= \sqrt{49}\sqrt{-1}\\[4pt] &= 7i \end{align*}$$

Ми використовуємо$7i$ і не$−7i$ тому, що основним коренем$49$ є позитивний корінь.

Комплексне число - це сума дійсного числа і уявного числа. Комплексне число виражається в стандартній формі при$a$ написанні,$a+bi$ де дійсна частина і$b$ є уявною частиною. Наприклад,$5+2i$ це комплексне число. Так, теж є$3+4i\sqrt{3}$.

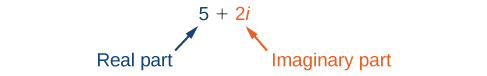
Уявні числа відрізняються від дійсних чисел тим, що квадратне уявне число виробляє від'ємне дійсне число. Нагадаємо, що коли позитивне дійсне число знаходиться в квадраті, результатом є додатне дійсне число, а коли негативне дійсне число знаходиться в квадраті, результатом є також позитивне дійсне число. Комплексні числа складаються з дійсних і уявних чисел.

Визначення: УЯВНІ І СКЛАДНІ ЧИСЛА

Комплексне число - це число форми,$a+bi$ де

1. $a$дійсна частина комплексного числа.
2. $b$уявна частина комплексного числа.

Якщо$b=0$, то$a+bi$ є дійсним числом. Якщо$a=0$ і не$b$ дорівнює$0$, комплексне число називається чистим уявним числом. Уявне число - парний корінь від'ємного числа.

Howto: Задано уявне число, висловити його в стандартній формі комплексного числа

1. Напишіть$\sqrt{-a}$ як$\sqrt{a}\sqrt{-1}$.
2. Експрес$\sqrt{-1}$ як$i$.
3. Пишіть$\sqrt{a}\times i$ в найпростішій формі.

Приклад$\PageIndex{1}$: Expressing an Imaginary Number in Standard Form

Експрес$\sqrt{-9}$ в стандартній формі.

Рішення

$$\begin{align*} \sqrt{-9}&= \sqrt{9}\sqrt{-1)}\\[4pt] &= 3i\\[4pt] \end{align*}$$

У стандартному вигляді це і є$0+3i$.

Вправа$\PageIndex{1}$

Експрес$\sqrt{-24}$ в стандартній формі.

Відповідь

$\sqrt{-24}=0+2i\sqrt{6}$

Побудова комплексного числа на комплексній площині

Ми не можемо побудувати складні числа на числовому рядку, як ми могли б реальні числа. Однак ми все ще можемо представити їх графічно. Щоб уявити комплексне число, нам потрібно звернутися до двох складових числа. Ми використовуємо складну площину, яка є системою координат, в якій горизонтальна вісь представляє дійсну складову, а вертикальна вісь - уявну складову. Комплексні числа - це точки на площині, виражені у вигляді впорядкованих пар$(a,b)$, де$a$ представляє координату горизонтальної осі і$b$ представляє координату для вертикальної осі.

Розглянемо число$−2+3i$. Реальна частина комплексного числа є,$−2$ а уявна частина -$3$. Ми будуємо впорядковану пару,$(−2,3)$ щоб представляти комплексне число$−2+3i$, як показано на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$

СКЛАДНА ПЛОЩИНА

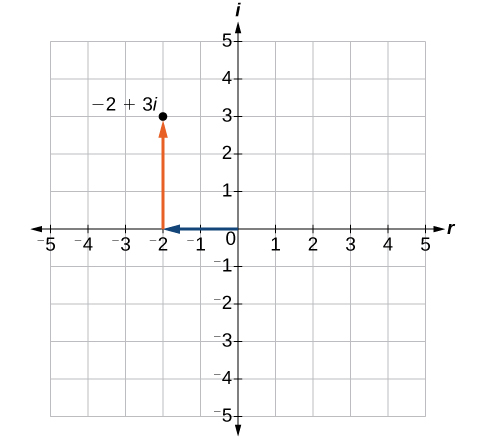
У складній площині горизонтальна вісь - це реальна вісь, а вертикальна - уявна вісь, як показано на малюнку$\PageIndex{3}$.

Малюнок$\PageIndex{3}$

Інструкція: Задано комплексне число, представляємо його складові на комплексній площині

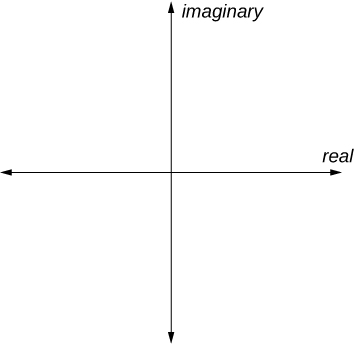
1. Визначте дійсну частину і уявну частину комплексного числа.
2. Рухайтеся вздовж горизонтальної осі, щоб показати дійсну частину числа.
3. Рухайтеся паралельно вертикальній осі, щоб показати уявну частину числа.
4. Помістіть крапку.

Приклад$\PageIndex{2}$: Plotting a Complex Number on the Complex Plane

Покладіть комплексне число$3−4i$ на комплексній площині.

Рішення

Реальна частина комплексного числа - це$3$, а уявна частина -$–4$. Розкладаємо впорядковану пару$(3,−4)$ так, як показано на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{4}$

Вправа$\PageIndex{2}$

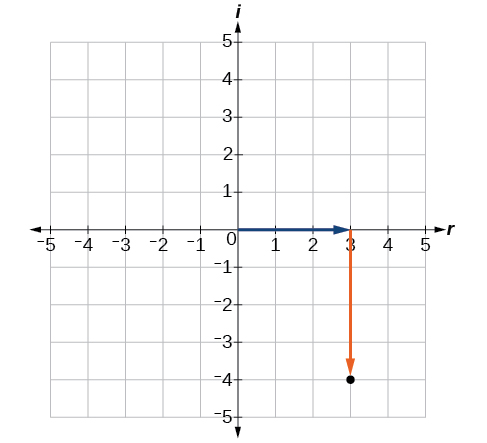
Покладіть комплексне число$−4−i$ на комплексній площині.

Відповідь

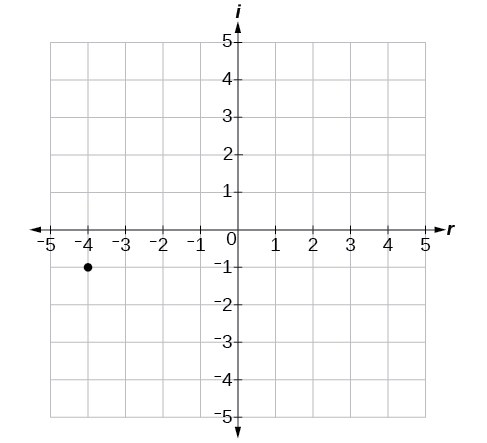
Малюнок$\PageIndex{5}$

Додавання та віднімання комплексних чисел

Так само, як і з дійсними числами, ми можемо виконувати арифметичні операції над комплексними числами. Щоб скласти або відняти комплексні числа, ми об'єднуємо дійсні частини, а потім об'єднуємо уявні частини.

КОМПЛЕКСНІ ЧИСЛА: ДОДАВАННЯ І ВІДНІМАННЯ

Додавання комплексних чисел:

$$(a+bi)+(c+di)=(a+c)+(b+d)i$$

Віднімання комплексних чисел:

$$(a+bi)−(c+di)=(a−c)+(b−d)i$$

Howto: За даними двох комплексних чисел знайдіть суму або різницю

1. Визначте реальну і уявну частини кожного числа.
2. Додайте або відніміть реальні частини.
3. Додайте або відніміть уявні частини.

Приклад$\PageIndex{3}$: Adding and Subtracting Complex Numbers

Додайте або відніміть, як зазначено.

1. $(3−4i)+(2+5i)$
2. $(−5+7i)−(−11+2i)$

Рішення

1. $$\begin{align*} (3-4i)+(2+5i)&= 3-4i+2+5i\\[4pt] &= 3+2+(-4i)+5i\\[4pt] &= (3+2)+(-4+5)i\\[4pt] &= 5+i \end{align*}$$
2. $$\begin{align*} (-5+7i)-(-11+2i)&= -5+7i+11-2i\\[4pt] &= -5+11+7i-2i\\[4pt] &= (-5+11)+(7-2)i\\[4pt] &= 6+5i \end{align*}$$

Вправа$\PageIndex{3}$

Відняти$2+5i$ від$3–4i$.

Відповідь

$(3−4i)−(2+5i)=1−9i$

Множення комплексних чисел

Множення комплексних чисел дуже схоже на множення бічленів. Основна відмінність полягає в тому, що ми працюємо з реальною і уявною частинами окремо.

Множення комплексного числа на дійсне число

Почнемо з множення комплексного числа на дійсне число. Ми розподіляємо дійсне число так само, як ми б з біноміальним. Розглянемо, наприклад,$3(6+2i)$:

Howto: Задано комплексне число та дійсне число, помножте, щоб знайти добуток

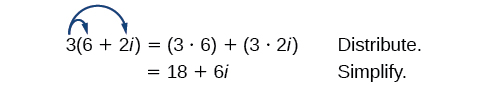
1. Використовувати розподільне властивість.
2. Спростити.

Приклад$\PageIndex{4}$: Multiplying a Complex Number by a Real Number

Знайдіть товар$4(2+5i)$.

Рішення

Розподіліть$4$.

$$\begin{align*} 4(2+5i)&= (4\cdot 2)+(4\cdot 5i)\\[4pt] &= 8+20i \end{align*}$$

Вправа$\PageIndex{4}$

Знайдіть товар:$\dfrac{1}{2}(5−2i)$.

Відповідь

$\dfrac{5}{2}-i$

Множення комплексних чисел разом

Тепер давайте помножимо два комплексних числа. Ми можемо використовувати або дистрибутивну властивість, або конкретніше метод FOIL, оскільки ми маємо справу з біномами. Нагадаємо, що FOIL є абревіатурою для множення Перший, Внутрішній, Зовнішній і Останній терміни разом. Різниця з комплексними числами полягає в тому, що коли ми отримуємо квадрат термін$i^2$, він дорівнює$-1$.

$$\begin{align*} (a+bi)(c+di)&= ac+adi+bci+bdi^2\\[4pt] &= ac+adi+bci-bd(-1)\qquad i^2 = -1\\[4pt] &= ac+adi+bci-bd\\[4pt] &= (ac-bd)+(ad+bc)i \end{align*}$$

Групуйте реальні терміни і уявні терміни.

Howto: Дано два комплексних числа, помножте, щоб знайти добуток

1. Використовуйте властивість distributive або метод FOIL.
2. Пам'ятайте про це$i^2=-1$.
3. Згрупуйте реальні терміни і уявні терміни

Приклад$\PageIndex{5}$: Multiplying a Complex Number by a Complex Number

Помножити$(4+3i)(2−5i)$.

Рішення

$$\begin{align*} (4+3i)(2-5i)&= 4(2)-4(5i)+3i(2)-(3i)(5i)\\[4pt] &= 8-20i+6i-15(i^2)\\[4pt] &= (8+15)+(-20+6)i\\[4pt] &= 23-14i \end{align*}$$

Вправа$\PageIndex{5}$

Помножити:$(3−4i)(2+3i)$.

Відповідь

$18+i$

Ділення комплексних чисел

Розділення двох комплексних чисел складніше, ніж додавання, віднімання або множення, оскільки ми не можемо розділити на уявне число, тобто будь-який дріб повинен мати знаменник дійсного числа, щоб написати відповідь у стандартній формі$a+bi$. Нам потрібно знайти термін, на який ми можемо помножити чисельник і знаменник, який усуне уявну частину знаменника, так що в кінцевому підсумку ми отримаємо дійсне число як знаменник. Цим терміном називають комплексний сполучений знаменник, який знаходить шляхом зміни знака уявної частини комплексного числа. Іншими словами, складний сполучений з$a+bi$ є$a−bi$. Наприклад, продукт$a+bi$ і$a−bi$ є

$$\begin{align*} (a+bi)(a-bi)&= a^2-abi+abi-b^2i^2\\[4pt] &= a^2+b^2 \end{align*}$$

В результаті виходить дійсне число.

Зверніть увагу, що складні кон'югати мають протилежний зв'язок: складний сполучений з$a+bi$ є$a−bi$, а складний сполучений з$a−bi$ є$a+bi$. Далі, коли квадратне рівняння з дійсними коефіцієнтами має складні розв'язки, розв'язки завжди є складними сполученнями один одного.

Припустимо, ми хочемо розділити$c+di$ на$a+bi$, де$a$ ні$b$ дорівнює нулю. Спочатку пишемо ділення у вигляді дробу, потім знаходимо складний сполучений знаменника, і множимо.

$\dfrac{c+di}{a+bi}$де$a≠0$ і$b≠0$

Помножте чисельник і знаменник на складний сполучений знаменника.

$$\begin{align*} \dfrac{(c+di)}{(a+bi)}\cdot \dfrac{(a-bi)}{(a-bi)}&= \dfrac{(c+di)(a-bi)}{(a+bi)(a-bi)}\\[4pt] &= \dfrac{ca-cbi+adi-bdi^2}{a^2-abi+abi-b^2i^2} \qquad \text{Apply the distributive property}\\[4pt] &= \dfrac{ca-cbi+adi-bd(-1)}{a^2-abi+abi-b^2(-1)} \qquad \text{Simplify, remembering that } i^2=-1\\[4pt] &= \dfrac{(ca+bd)+(ad-cb)i}{a^2+b^2} \end{align*}$$

Визначення: СКЛАДНЕ СПОЛУЧЕННЯ

Складний сполучений комплексного числа$a+bi$ є$a−bi$. Його знаходять шляхом зміни знака уявної частини комплексного числа. Реальну частину числа залишають без змін.

1. Коли комплексне число множиться на його комплексний сполучений, в результаті виходить дійсне число.
2. При додаванні комплексного числа до його складного сполученого результату виходить дійсне число.

Приклад$\PageIndex{6}$: Finding Complex Conjugates

Знайти складний сполучений кожного числа.

1. $2+i\sqrt{5}$
2. $-\dfrac{1}{2}i$

Рішення

1. Число вже в формі$a+bi$. Складний сполучений є$a−bi$, або$2−i\sqrt{5}$.
2. Ми можемо переписати це число у вигляді$a+bi$ як$0−\dfrac{1}{2}i$. Складний сполучений є$a−bi$, або$0+\dfrac{1}{2}i$. Це можна написати просто як$\dfrac{1}{2}i$.

Аналіз

Хоча ми бачили, що ми можемо знайти складний сполучений уявного числа, на практиці ми, як правило, знаходимо комплексні сполучення тільки комплексних чисел як з дійсною, так і з уявною складовою. Щоб отримати дійсне число з уявного числа, ми можемо просто помножити на$i$.

Вправа$\PageIndex{6}$

Знайти складний сполучений з$−3+4i$.

Відповідь

$−3−4i$

Як: Дано два комплексних числа, розділіть одне на інше

1. Запишіть задачу ділення як дріб.
2. Визначте складне сполучення знаменника.
3. Помножте чисельник і знаменник дробу на складний сполучений знаменника.
4. Спростити.

Приклад$\PageIndex{7}$: Dividing Complex Numbers

Розділити$(2+5i)$ на$(4−i)$.

Рішення

Почнемо з написання завдання як дріб.

$$\dfrac{(2+5i)}{(4−i)} \nonumber$$

Потім чисельник і знаменник множимо на комплексний сполучений знаменника.

$$\dfrac{(2+5i)}{(4−i)}⋅\dfrac{(4+i)}{(4+i)} \nonumber$$

Щоб помножити два комплексних числа, ми розгортаємо твір так само, як і з поліномами (за допомогою FOIL).

$$\begin{align*} \dfrac{(2+5i)}{(4-i)}\cdot \dfrac{(4+i)}{(4+i)}&= \dfrac{8+2i+20i+5i^2}{16+4i-4i-i^2}\\[4pt] &= \dfrac{8+2i+20i+5(-1)}{16+4i-4i-(-1)}\; i^2=-1 \\[4pt] &= \dfrac{3+22i}{17}\\[4pt] &= \dfrac{3}{17}+\dfrac{22}{17i} \end{align*}$$

Відокремлюють реальну і уявну частини.

Зверніть увагу, що це виражає частку в стандартній формі.

Спрощення повноважень$i$

Повноваження$i$ циклічні. Давайте розглянемо, що відбувається, коли ми піднімемося$i$ до збільшення повноважень.

$$i^1=i \nonumber$$ $$i^2=-1 \nonumber$$ $$i^3=i^2⋅i=-1⋅i=-i \nonumber$$ $$i^4=i^3⋅i=-i⋅i=-i^2=-(-1)=1 \nonumber$$ $$i^5=i^4⋅i=1⋅i=i \nonumber$$

Ми бачимо, що коли ми доходимо до п'ятої потужності i, вона дорівнює першій потужності. Оскільки ми продовжуємо$i$ множитися на збільшення повноважень, ми побачимо цикл з чотирьох. Давайте розглянемо наступні чотири повноваження$i$.

$$i^6=i^5⋅i=i⋅i=i^2=-1 \nonumber$$ $$i^7=i^6⋅i=i^2⋅i=i^3=-i \nonumber$$ $$i^8=i^7⋅i=i^3⋅i=i^4=1 \nonumber$$ $$i^9=i^8⋅i=i^4⋅i=i^5=i \nonumber$$

Цикл повторюється безперервно:$i,−1,−i,1,$ кожні чотири сили.

Приклад$\PageIndex{8}$: Simplifying Powers of $i$

Оцініть:$i^{35}$.

Рішення

Так як$i^4=1$, ми можемо спростити проблему, враховуючи$i^4$ якомога більше факторів. Для цього спочатку визначте, скільки разів$4$ переходить$35: 35=4⋅8+3$.

$$i^{35}=i^{4⋅8+3}=i^{4⋅8}⋅i^3={(i^4)}^8⋅i^3=i^8⋅i^3=i^3=−i \nonumber$$

Вправа$\PageIndex{7}$

Оцініть:$i^{18}$

Відповідь

$−1$

Q&A

Чи можемо ми писати$i^{35}$ іншими корисними способами?

Як ми бачили в прикладі$\PageIndex{8}$, ми зведені$i^{35}$ до,$i^3$ діливши показник на$4$ і використовуючи залишок, щоб знайти спрощену форму. Але, можливо, інша факторизація$i^{35}$ може виявитися більш корисною. Таблиця$\PageIndex{1}$ показує деякі інші можливі факторизації.

Таблиця$\PageIndex{1}$

Факторизація$i^{35}$	$i^{34}⋅i$	$i^{33}⋅i^2$	$i^{31}⋅i^4$	$i^{19}⋅i^{16}$
Зменшена форма	${(i^2)}^{17}⋅i$	$i^{33}⋅(−1)$	$i^{31}⋅1$	$i^{19}⋅{(i^4)}^4$
Спрощена форма	${(−1)}^{17}⋅i$	$−i^{33}$	$i^{31}$	$i^{19}$

Кожен з них врешті-решт призведе до відповіді, яку ми отримали вище, але може знадобитися кілька кроків, ніж наш попередній метод.

Медіа

Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики зі складними числами.

1. Додавання та віднімання комплексних чисел
2. Множення комплексних чисел
3. Множення складних кон'югатів
4. Підвищення його до повноважень

Ключові концепції

• Квадратний корінь будь-якого від'ємного числа може бути записаний кратним \(i\). Див. Приклад.
• Для побудови комплексного числа використовуємо дві числові лінії, перехрещені для формування комплексної площини. Горизонтальна вісь - це реальна вісь, а вертикальна - уявна вісь. Див. Приклад.
• Комплексні числа можна додавати і віднімати шляхом об'єднання дійсних частин і комбінування уявних частин. Див. Приклад.
• Комплексні числа можна множити і ділити.
  • Щоб помножити комплексні числа, розподіліть так само, як і з многочленами. Див. Приклад і Приклад.
  • Для поділу комплексних чисел помножте і чисельник, і знаменник на комплексне сполучення знаменника, щоб виключити комплексне число зі знаменника. Див. Приклад і Приклад.
• Сили i циклічні, повторюючи кожну четверту. Див. Приклад.