7.1: Основний принцип підрахунку
- Page ID
- 58789
Комбінаторика є основною областю того, що, як правило, відомий як «Дискретна математика». Слово дискретне відноситься до величин, які є індивідуальними, окремими або різними. Це створює великий поділ в математиці між «безперервною математикою» та «дискретною математикою». Різниця між цими двома областями полягає в тому, що безперервна математика розглядає і використовує всі частини числового рядка цілі числа, раціональні числа (дроби), ірраціональні числа і так далі. Дискретна математика зазвичай використовує тільки цілі числа.
Замість того, щоб обмежувати можливості в математиці, це обмеження насправді відкриває дивовижні нові сфери розгляду. Двійкові коди, які використовують комп'ютери, як правило, контролюються і зберігаються (в основному) без помилок завдяки використанню дискретної математики. Комп'ютерна безпека для найпростішої (перевірка вашого он-лайн банківського балансу) та найскладнішої (класифіковані дані високого рівня) цифрової інформації обробляється за допомогою шифрування, яке спирається на поняття дискретної математики.
Будь-який тип застосування в науках, який передбачає вибір і можливості, часто використовує поняття комбінаторики. Комбінаторна хімія досліджує результати, коли до однієї і тієї ж основної хімічної структури додається ряд різних хімічних груп для дослідження якостей отриманої сполуки. Крім того, комбінаторика дуже важлива для вивчення ймовірності. Для того щоб обчислити ймовірність події, часто доводиться підрахувати, скільки
по-різному щось може статися.
Першою основною ідеєю комбінаторики є основоположний принцип підрахунку. Це ідея, що якщо дві події відбуваються послідовно і є\(m\) способи зробити першу і\(n\) способи зробити другу (після того, як відбулося перше), то є\(m * n\) способи виконати два завдання послідовно.
Наприклад, в киданні двох шестигранних кубиків передбачено 36 можливостей - шість можливостей з першого кубика і шість з другого. Ці можливості перераховані нижче:

Якби ми кинули шестигранну матрицю та восьмисторонню матрицю, то були б\(6 * 8=48\) різні можливості.
Часто створення діаграми дерева може допомогти нам візуалізувати можливості. Припустимо, що тризначний код з використанням цифр 0,1 і 2 створений так, щоб допускалося повторення чисел. Було б 3 можливості для першого числа, три для другого числа і три для третього числа, що означає, що буде загальна кількість\(3 * 3 * 3=27\) різних можливих кодів.
Деревоподібна діаграма, яка ілюструє це, показано на наступній сторінці.
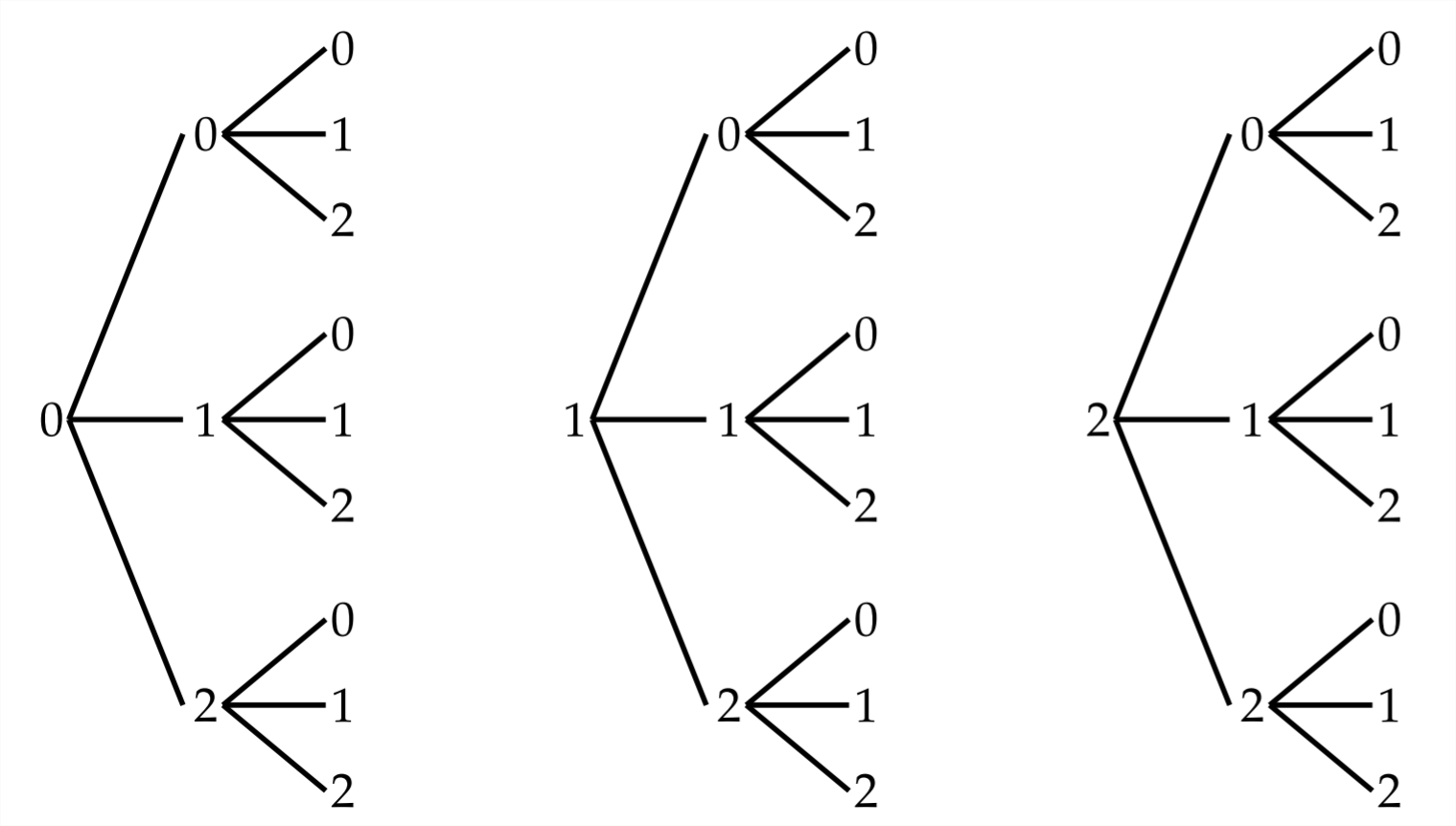
Всі можливості перераховані і можуть бути побудовані на основі діаграми дерева.
Ось деякі приклади задач для використання фундаментального принципу підрахунку (також відомий як принцип множення).
Приклад: У магазині морозива пропонують морозиво «Ваніль», «Шоколад», «Полуниця», «Бойзенберрі» та «Роккі Морозиво поставляється з вафельним конусом, цукровим конусом або вафельним конусом і може бути простим або з посипками. Скільки існує різних способів замовити одну кульку морозива?
З 5 різними видами морозива, 3 різними конусами та 2 варіантами для посипання, були б\(5 * 3 * 2=30\) різні можливості.
Приклад:
У багатьох штатах номерні знаки для автомобілів складаються з трьох букв, за якими слідують три цифри.
Скільки різних можливостей:
якщо допускається повторення букв і цифр?
якщо повторення букв і цифр не допускається?
Існує шість позицій для букв і цифр, які складають номерний знак.
Перші три повинні бути буквами, а другі три цифри.
Є 26 варіантів для перших трьох і 10 варіантів для других трьох, тому\(26 * 26 * 26 * 10 * 10 * 10=17,576,000\) можливі номерні знаки, якщо дозволено повторення.
Якщо повторення не допускається, то ми повинні знижувати будь-яку букву або цифру, обрану для певної позиції. Так, для першої літери існує 26 можливостей, але потім тільки 25 для другої літери і 24 для третьої. Так само з числами спочатку є 10 варіантів, потім 9 варіантів, а потім 8
Отже, рішення без повторення було б\(26 * 25 * 24 * 10 * 9 * 8=11,232,000\)
4)\(\quad\) Монета перевертається п'ять разів і кожен раз записується результат. Скільки різних можливих результатів існує?
5)\(\quad\) Перевертається монета і прокочується шестигранна плашка і записуються результати. Якщо це зробити три рази, скільки можливих результатів є?
6)\(\quad\) Дві карти вибираються з колоди з 52 карт. Якщо перша карта не замінена до вибору другої карти, скільки способів вибрати:
а)\(\quad\) Лопата перша і серце друга?
б)\(\quad\) Дві лопати?
7) Компанія\(\quad\) має 3000 співробітників. Вони планують впровадити систему нумерації ідентифікаторів співробітників, яка б складалася з літери, за якою слідують дві цифри. Чи можна дати кожному співробітнику інший ідентифікаційний код за цим планом?
8)\(\quad\) Бейсбольна команда має 7 глечиків і 3 ловців. Скільки різних акумуляторів (комбінацій глечик - уловлювач) можливі?
9)\(\quad\) Рядок з п'яти букв створюється за допомогою букв\(\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}\) і Е. Скільки з цих рядків літер можливо, якщо:
\(\quad\) а)\(\quad\) Ніякі умови не накладаються
\(\quad\) б) Повторення\(A\) літери не допускається
\(\quad\)c) Кожна буква рядок повинна починатися з\(C\)
\(\quad\) d)\(\quad\) B повинна бути середньою літерою
\(\quad\) е)\(\quad\)\(A, B\) і\(C\) повинна бути середніми літерами в будь-якому порядку без повторення
For Part ( д) будь ласка, перерахуйте всі можливості.
10) (\ quad\) Кодовий замок пронумерований від 0 до 30. Кожна комбінація складається з трьох чисел поспіль. Послідовні числа повинні бути різними, але перше і третє можуть бути однаковими. Скільки різних комбінацій можливо?
