10.2: Розв'язування квадратних рівнянь
- Page ID
- 58500
Стандартна форма квадратного рівняння
У главі 5 ми вивчали лінійні рівняння в одній і двох змінних і методи їх розв'язання. Ми спостерігали, що лінійне рівняння в одній змінній - це будь-яке рівняння, яке можна записати у формі\(ax + b = 0, a\not = 0\), а лінійне рівняння у двох змінних - будь-яке рівняння, яке можна записати у вигляді\(ax + by = c\), де\(a\) і не\(b\) обидва\(0\). Тепер ми хочемо вивчити квадратні рівняння в одній змінній.
Квадратне рівняння - рівняння виду\(ax^2 + bx + c = 0, a \not = 0\).
Стандартною формою квадратного рівняння є\(ax^2 + bx + c = 0, a \not = 0\).
Для квадратного рівняння в стандартній формі\(ax^2 + bx + c = 0\)
\(a\)це коефіцієнт\(x^2\).
\(b\)це коефіцієнт\(x\).
\(c\)є постійним терміном.
Набір зразків A
Нижче наведені квадратні рівняння.
\(3x^2 + 2x - 1 = 0\). \(a = 3, b = 2, c = -1\)
\(5x^2 + 8x = 0\). \(a = 5, b = 8, c = 0\)
Зверніть увагу, що це рівняння може бути записано\(5x^2 + 8x + 0 = 0\). Тепер зрозуміло, що\(c = 0\).
\(x^2 + 7 = 0\). \(a = 1, b = 0, c = 7\).
Зверніть увагу, що це рівняння може бути записано\(x^2 + 0x + 7 = 0\). Тепер зрозуміло, що\(b = 0\)
Нижче наведені не квадратні рівняння.
\(3x + 2 = 0\). \(a = 0\). Це рівняння лінійне.
\(8x^2 + \dfrac{3}{x} - 5 = 0\)
Вираз з лівого боку знака рівності має змінну в знаменнику і, отже, не є квадратичним.
Практика Set A
Які з наступних рівнянь є квадратними рівняннями? Відповідь «так» або «ні» на кожне рівняння.
\(6x^2 - 4x + 9 = 0\)
- Відповідь
-
так
\(5x+8=0\)
- Відповідь
-
ні
\(4x^3 - 5x^2 + x + 6 = 8\)
- Відповідь
-
ні
\(4x^2 - 2x + 4 = 1\)
- Відповідь
-
так
\(\dfrac{2}{x} - 5x^2 = 6x + 4\)
- Відповідь
-
ні
\(9x^2 - 2x + 6 = 4x^2 + 8\)
- Відповідь
-
так
Нерухомість з нульовим фактором
Наша мета - розв'язувати квадратні рівняння. Метод розв'язання квадратичних рівнянь заснований на нульовій факторній властивості дійсних чисел. Ми познайомилися з властивістю нульового фактора в розділі 8.2. Ми заявляємо про це ще раз.
Якщо два числа\(a\) і\(b\) множаться разом і отримане добуток є\(0\), то хоча б одне з чисел повинно бути\(0\). Алгебраїчно, якщо\(a \cdot b = 0\), то\(a = 0\) або обидва\(a = 0\) і\(b = 0\).
Набір зразків B
Використовуйте властивість нульового фактора для вирішення кожного рівняння.
Якщо\(9x = 0\), то\(x\) обов'язково\(0\).
Якщо\(-2x^2 = 0\), то\(x^2 = 0, x = 0\)
Якщо\(5\) то\(x-1\) повинно бути\(0\), так як не\(5\) дорівнює нулю.
\ (\ begin {масив} {Flushleft}
х - 1 &= 0\\
x &= 1
\ end {масив}\)
Якщо\(x(x+6) = 0\), то
\ (\ begin {масив} {Flushleft}
х &= 0 &\ текст {або} & x+6&= 0\\ x
& = 0, -6 && x &= -6
\ end {масив}\)
Якщо\((x+2)(x+3) = 0\), то
\ (\ begin {масив} {Flushleft}
х + 2 &= 0 &\ текст {або} & x + 3 &= 0\\
x &= -2 && x = -3\
x &= -2, -3
\ end {масив}\)
Якщо\((x+10)(4x - 5) = 0\), то
\ (\ почати {масив} {змивний лівий}
х + 10 &= 0 &\ текст {або} & 4x - 5 &= 0\\
x &= -10 & 4x &= 5\
x &= -10,\ dfrac {5} {4} &&=\ dfrac {5} {4}
\ кінець {масив}\)
Практика Set B
Використовуйте властивість нульового фактора для вирішення кожного рівняння.
\(6(a−4)=0\)
- Відповідь
-
\(a=4\)
\((y+6)(y−7)=0\)
- Відповідь
-
\(y=−6, 7\)
\((x+5)(3x−4)=0\)
- Відповідь
-
\(x = -5, \dfrac{4}{3}\)
Вправи
Для наступних задач запишіть значення\(a\)\(b\), і\(c\) в квадратних рівняннях.
\(3x^2 + 4x - 7 = 0\)
- Відповідь
-
\(3,4,−7\)
\(7x^2 + 2x + 8 = 0\)
\(2y^2 - 5y + 5 = 0\)
- Відповідь
-
\(2,−5,5\)
\(7a^2 + a - 8 = 0\).
\(-3a^2 + 4a - 1 = 0\)
- Відповідь
-
\(−3,4,−1\)
\(7b^2 + 3b + 0\)
\(2x^2 + 5x + 0\)
- Відповідь
-
\(2, 5, 0\)
\(4y^2 + 9 = 0\)
\(8a^2 - 2a = 0\)
- Відповідь
-
\(8,−2,0\)
\(6x^2 = 0\)
\(4y^2 = 0\)
- Відповідь
-
\(4, 0, 0\)
\(5x^2 - 3x + 9 = 4x^2\)
\(7x^2 + 2x + 1 = 6x^2 + x - 9\)
- Відповідь
-
\(1, 1, 10\)
\(-3x^2 + 4x - 1 = -4x^2 - 4x + 12\)
\(5x - 7 = -3x^2\)
- Відповідь
-
\(3,5,−7\)
\(3x - 7 = -2x^2 + 5x\)
\(0 = x^2 + 6x - 1\)
- Відповідь
-
\(1,6,−1\)
\(9 = x^2\)
\(x^2 = 9\)
- Відповідь
-
\(1,0,−9\)
\(0 = -x ^2\)
Для наступних задач використовуйте властивість нульового фактора для розв'язання рівнянь.
\(4x = 0\)
- Відповідь
-
\(x=0\)
\(16y=0\)
\(9a=0\)
- Відповідь
-
\(a=0\)
\(4m=0\)
\(3(k+7)=0\)
- Відповідь
-
\(k=−7\)
\(8(y−6)=0\)
\(−5(x+4)=0\)
- Відповідь
-
\(x=−4\)
\(−6(n+15)=0\)
\(y(y−1)=0\)
- Відповідь
-
\(y=0,1\)
\(a(a−6)=0\)
\(n(n+4)=0\)
- Відповідь
-
\(n=0,−4\)
\(x(x+8)=0\)
\(9(a−4)=0\)
- Відповідь
-
\(a=4\)
\(−2(m+11)=0\)
\(x(x+7) = 0\)
- Відповідь
-
\(x=−7 \text{ or } x=0\)
\(n(n−10)=0\)
\((y−4)(y−8)=0\)
- Відповідь
-
\(y=4 \text{ or } y=8\)
\((k−1)(k−6)=0\)
\((x+5)(x+4)=0\)
- Відповідь
-
\(x=−4 \text{ or } x=−5\)
\((y+6)(2y+1)=0\)
\((x−3)(5x−6)=0\)
- Відповідь
-
\(x = \dfrac{6}{5} \text{ or } x = 3\)
\((5a+1)(2a−3)=0\)
\((6m+5)(11m−6)=0\)
- Відповідь
-
\(m = -\dfrac{5}{6} \text{ or } m = \dfrac{6}{11}\)
\((2m−1)(3m+8)=0\)
\((4x+5)(2x−7)=0\)
- Відповідь
-
\(x = \dfrac{-5}{4}, \dfrac{7}{2}\)
\((3y + 1)(2y + 1) = 0\)
\((7a + 6)(7a - 6) = 0\)
- Відповідь
-
\(a = \dfrac{-6}{7}, \dfrac{6}{7}\)
\((8x+11)(2x−7)=0\)
\((5x−14)(3x+10)=0\)
- Відповідь
-
\(x = \dfrac{14}{5}, \dfrac{-10}{3}\)
\((3x−1)(3x−1)=0\)
\((2y+5)(2y+5)=0\)
- Відповідь
-
\(y = \dfrac{-5}{2}\)
\((7a - 2)^2 = 0\)
\((5m - 6)^2 = 0\)
- Відповідь
-
\(m = \dfrac{6}{5}\)
Вправи для огляду
Фактор\(12ax - 3x + 8a - 2\) за групуванням.
Побудувати граф\(6x + 10y - 60 = 0\)
- Відповідь
-
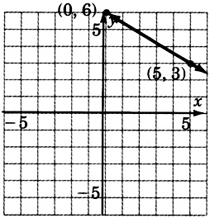
Знайдіть різницю:\(\dfrac{1}{x^2 + 2x + 1} - \dfrac{1}{x^2 - 1}\).
Спростити\(\sqrt{7}(\sqrt{2} + 2)\)
- Відповідь
-
\(\sqrt{14} + 2\sqrt{7}\)
Вирішити радикальне рівняння\(\sqrt{3x + 10} = x + 4\)
