6.1: Проблеми

1. (а) Встановити всі абстрактні групи, що мають порядок$2 \le N \le 6$. Обчислити типові продукти. Які групи є Абелеви? Вкажіть принаймні дві ізоморфні реалізації для кожної групи.

   (b) Визначте підгрупи. Які є інваріантними?

2. Запишіть перестановки$n = 3$ і$n = 4$ об'єктів. Оформіть результат компактно. Розглянемо спочатку підгрупу парних перестановок (чергуються групи). Скористайтеся циклами.
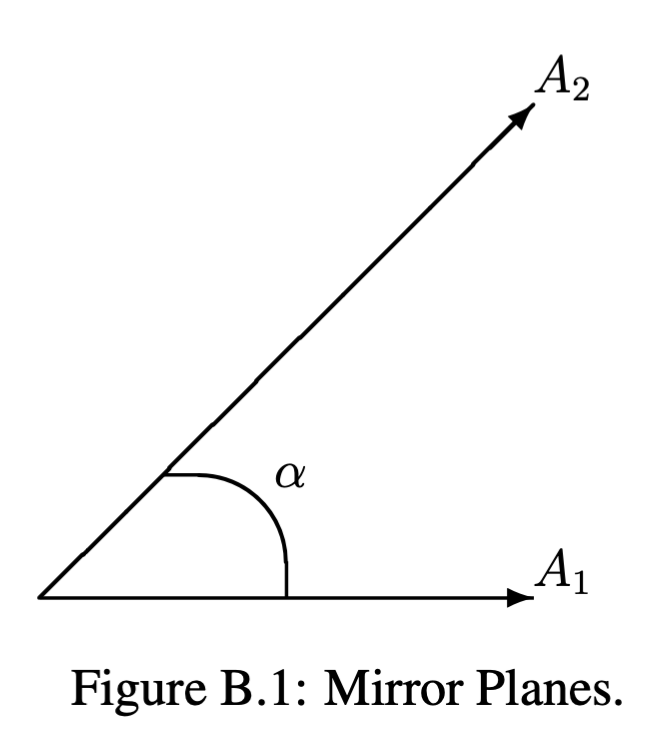
3. Знайдіть спільний ефект двох дзеркальних площин (див. Рис. Розглянемо також паралельні дзеркала.

   

4. Сферичний хвильовий імпульс розходиться від просторово-часової точки (0, 0, 0, 0) в інерційній рамці$\sum$. Розглянемо кадр, що$\sum'$ рухається вздовж напрямку z зі швидкістю$\beta = \tanh \mu$. Спостерігач в$\sum'$ бачить також сферичні хвильові фронти. Однак просторово-часові точки, що складають поверхню,$r' = ct' = const$ не виглядають синхронно, отже, сферичні$\sum$. Показати, що поверхні є еліпсоїдами обертання з одним загальним фокусом. Знайти великі і другорядні осі a, b, і ексцентриситет з точки зору$r'$ і$\beta$. Знайдіть також довжини перигелія і афелія. Використовуйте полярні координати.
5. Розглянемо склад ротацій в$\mathcal{SU}(2)$ формалізмі:$U'' =U'U$ де$U = l_{0} = -i \vec{l} \cdot \vec{\sigma}$, з

$$\begin{array}{cc} {l_{0} = \cos \frac{\phi}{2},}&{\vec{l} = \sin \frac{\phi}{2} \hat{u}} \nonumber \end{array}$$

(а) Експрес з$\{l_{0}'', \vec{l}''\}$ точки зору$\{l_{0}', \vec{l}'\}$ і$\{l_{0}, \vec{l}\}$.

(b) Зверніться до теореми Родрієса-Гамільтона (рис. 2.1) та отримайте косинусний закон сферичної тригонометрії.

(c) Отримати закон синуса.

6. Перевірте свої загальні вирази, застосувавши особливі випадки:

(а)$U'' = UU = U^{2}$

(б)$\hat{u} = \frac{1}{\sqrt{3}} (1, 1, 1),}&{\phi = \frac{2 \pi}{3}$

$\hat{u} = \frac{1}{\sqrt{3}} (1, 0, 0),}&{\phi = \frac{\pi}{2}$

Зауважте, що U і U 'генерують операції симетрії на кубі.

7. Розглянемо одновимірний рух частинки спокою масою m, під впливом сили$eE_{z}$. У$t = 0$ частинки знаходиться в стані спокою. Покажіть, що траєкторія представлена в площині z, ct у вигляді гіперболи і знайдіть напівдіаметр. Розробіть аналогію з проблемою циклотрона, наскільки зможете. Обговоріть значення наближення

$$\begin{array}{c} {\gamma^{-1} = \sqrt{1-\beta^2} \simeq 1} \nonumber \end{array}$$

8. Розглянемо електромагнітне поле

$$\begin{array}{c} {\vec{f} = \vec{E}+i \vec{B}} \nonumber \end{array}$$

в невеликому просторово-часовому регіоні. Інваріант Лоренца поля:

$$\begin{array}{c} {f^{2} = E^{2}-B^{2}+2i E \cdot B = I_{1}+i I_{2} = g^{2} \exp(2i \psi)} \nonumber \end{array}$$

(а) Розглянемо випадок$f^{2} \ne 0$. У цьому випадку існує канонічний кадр, в якому$E_{can} \parallel B_{can}$ і$\zeta = B_{can}/E_{can}$, крок, є дійсним числом (яке може бути 0 або$\infty$). Обговоріть можливі значення$\zeta$ за ознаками$I_{1}$ і$I_{2}$. Підсумуйте свої висновки в таблиці, подібній до наведеної в таблиці B.1.

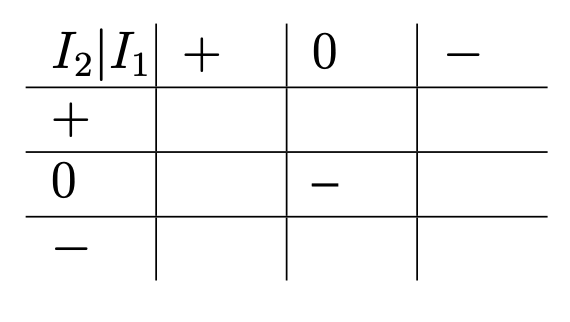
Таблиця B.1: Таблиця для завдання 8

(б) Експрес з$E_{can}, B_{can}, \zeta$ точки зору$I_{1}, I_{2}$ і$g, \psi$.

(c) Припустимо$\zeta \ne 0, \infty$. Візьміть$\hat{x}$ з собою$E_{can}$. Розглянемо пасивне перетворення Лоренца в$\hat{z}$ напрямку, до кадру швидкості$v(\beta = v/c = \tanh \mu)$ по відношенню до канонічного кадру. Знайти$\tan \theta E, \tan \theta B, \tan(\theta_{E}-\theta_{B})$ в терміні,$\beta, \zeta$ а також$\mu, \psi$, де$\theta_{E}$ і$\theta_{B}$ є кути, на які обертаються електричне і магнітне поля при перетворенні Лоренца, як показано на малюнку В.2.

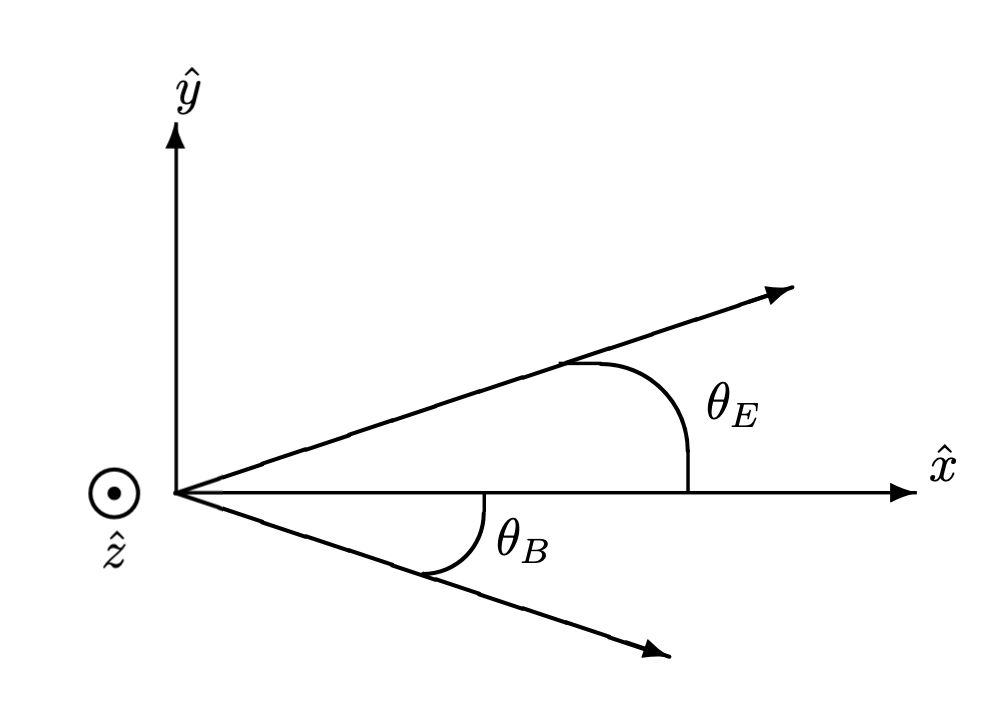
Малюнок В.2: Задача 8 координатний кадр і кути.

(d) Розглянемо зараз випадки$\zeta = 0; \zeta = \infty$. Візьміть$\hat{x}$ в сторону незникаючого канонічного поля. Обговоріть ефект перетворення Лоренца, подібний до того, що розглядається в (c). Дайте співвідношення величин електричного і магнітного полів після перетворення Лоренца.

9. (a) Знайти полярне розкладання матриці

$$\begin{array}{c} {\begin{pmatrix} {1}&{\zeta}\\ {0}&{1} \end{pmatrix}} \nonumber \end{array}$$

Перевірити співвідношення (11б) на стор II-53. Розглянемо випадки$\delta = 1$ і$\delta << 1$.

(б) Знайти

$$\begin{array}{c} {\mathcal{P}_{\hat{a}} (\vec{p} \cdot \vec{\sigma}) \mathcal{P}_{\hat{a}}} \nonumber \end{array}$$

де

$$\begin{array}{c} {\mathcal{P}_{\hat{a}} = \frac{1}{2} (1+\hat{a} \cdot \vec{\sigma})} \nonumber \end{array}$$

10. Перевірте Eq (23) - (26) на II-42, 43.

11. Показати, що матриця полів$F = (\vec{E}+i \vec{B}) \cdot \vec{\sigma}$ може бути виведена з матричного еквівалента чотирипотенціалу. Які умови, якщо такі є, повинні бути накладені останнім?

12. (а) Висловити відображення чотиривектора$K = k_{0}1+\vec{k} \cdot \vec{\sigma}$ в рухомій площині. Нормаль площини є$\hat{a}$. Його швидкість -$v = v \hat{a}$ с$v/c = \tanh \mu$. (Підказка: перетворити на решту кадру дзеркала.)

(б) Показати, що поєднання двох$\vec{v}_{1} = v_{1} \hat{a}_{1}$ дзеркал$\vec{v}_{2} = v_{2} \hat{a}_{2}$ дає і Лоренца перетворення.

13. Перевірте еквівалентність рівнянь (4) та (5) у розділі 4.2 шляхом перетворення кожного фактора від простору до корпусу.

14. Показати, що відношення

$$\begin{array}{c} {|\xi \rangle \langle \xi |= \frac{1}{2} (1+\hat{k} \cdot \vec{\sigma})} \end{array}$$

можна отримати за допомогою стереографічної проекції.

Підказка: Спроектуйте сферу$k_{1}^{2}+k_{2}^{2}+k_{3}^{2} = 1$ від південного полюса до екваторіальної площини, інтерпретовану як складну z-площину. Експрес з$k_{1}, k_{2}, k_{3}$ точки зору$z, z∗$ і набір$z = \xi_{1}/\xi_{0}$ с$|\xi_{0}|^{2}+|\xi_{1}|^{2} = 1$.

15. Знайдіть унітарну матрицю U, яка з'єднує два заданих множини спінорів між собою:

$$\begin{array}{c} {(| \eta \rangle, | \bar{\eta} \rangle) = (| \xi \rangle, | \bar{\xi} \rangle)U} \end{array}$$

Висловлюйте спочатку його елементи, потім його складові в плані$\xi_{0}, \xi_{1}, \eta_{0}, \eta_{1}$.

16. Алгебру Паулі можна розглядати як узагальнення елементарної векторної алгебри, і знання останньої корисно в матричних маніпуляціях.

Однак можна підійти до проблеми і з зворотної точки зору і вивести векторні відносини за допомогою матричних операцій. Визначте

$$\begin{array}{ccc} {A= \vec{a} \cdot \vec{\sigma},}&{B = \vec{b} \cdot \vec{\sigma},}&{C = \vec{c} \cdot \vec{\sigma}} \nonumber \end{array}$$

і асоційовані

$$\begin{array}{ccc} {\vec{a} \cdot \vec{b}}&{with}&{\frac{1}{2} \{A, B\} = \frac{1}{2} (AB+BA)} \end{array}$$

$$\begin{array}{ccc} {\vec{a} \times \vec{b}}&{with}&{\frac{1}{2i} \{A, B\} = \frac{1}{2i} (AB-BA)} \end{array}$$

Розглянемо ідентичність Якобі

$$\begin{array}{c} {[[A, B], C] + [[B, C], A] + [[C, A], B] = 0} \end{array}$$

і умова асоціативності:

$$\begin{array}{c} {A (BC)-(AB) C = 0} \end{array}$$

(Рівняння B.1.5 легко перевіряється для комутаторів. Про його значення див. [Hal74].)

Перевести рівняння B.1.5 та B.1.6 за допомогою рівнянь B.1.3 та B.1.4 та отримати знайомі співвідношення для потрійних векторних добутків.

17. Дайте явні спіноріальні вирази для наступних форм поляризації:$| x \rangle$ (лінійна поляризація по осі х);$| \theta/2 \rangle$ (поляризована під кутом$\theta /2$ з віссю х);$| R \rangle$ (права кругова поляризація).

(а) Скористайтеся$\hat{\kappa} (\phi, \theta, \psi)$ схемою та$\phi = \psi = \theta = 0$ призначте$| x \rangle = (1, 0)$. Експрес з$| \theta/2 \rangle, | \theta/2 \rangle, | R \rangle, | \bar{R} \rangle$ точки зору$| x \rangle$ і$| \bar{x} \rangle$.

(б) Скористайтеся$\hat{s}(\alpha, \beta, \gamma)$ схемою. Призначити$\beta = 0, \alpha = \gamma = \pi / 2$ до$| R \rangle$. Висловіть вищезгадані спінори з точки зору$| R \rangle$ і$| \bar{R} \rangle$. Зверніть увагу, що результати (a) і (b) узгоджуються один з одним.

18. Дайте матриці зображення чверті хвилі, пластини, полуволновой пластини, ротатора і плоского поляризатора в обох$\hat{k}$ і$\hat{s}$ схемах.

19. (a) Ми знаємо про оптичний інструмент лише те, що він$| R \rangle$ перетворюється на$| \bar{R} \rangle$ і навпаки. Знайдіть найбільш загальний матричний оператор, що відповідає цьому факту.

(б) Заточити цю відповідь, використовуючи додаткову інформацію про те, що прилад пропускає промінь$| x \rangle$ без змін. Як називається цей пристрій?

20. Розглянемо довільну ермітієву$2 \times 2$ матрицю:$S = s_{0}+\vec{s} \cdot \vec{\sigma}$ з$s_{0}^{2}-\vec{s}^{2} \ne 0$ в загальному.

(а) Показати, що можна розкласти S на суму двох матриць з детермінантним нулем. Тобто:

$$\begin{array}{c} {S = K'+K''} \nonumber \end{array}$$

де

$$\begin{array}{cc} {K' = k'_{0}+\vec{k}' \cdot \vec{\sigma}}&{k_{0}^{'2}-\vec{k}'^{2}} \nonumber \end{array}$$

$$\begin{array}{cc} {K'' = k''_{0}+\vec{k}'' \cdot \vec{\sigma}}&{k_{0}^{''2}-\vec{k}''^{2}} \nonumber \end{array}$$

(b) Показати, що якщо хтось нав'язує:

$$\begin{array}{c} {\vec{k}' = k' \hat{k}}\\ {\vec{k}'' = k'' \hat{k}}\\ {\vec{k}' and \vec{k}'' parallel} \nonumber \end{array}$$

розкладання стає унікальним. Знайти$k_{0}', k_{0}'', k', k'', hat{k}$.

21. Розглянемо приблизно монохроматичний промінь неполяризованого світла, було запропоновано розглядати такий промінь як випадкову послідовність еліптично поляризованого світла, завдяки чому параметри еліптичності$\alpha, \beta$ змінюються повільно порівняно з,$1/\omega$ але швидко в порівнянні з часом спостереження (див. 45]). Автор показує, що середня еліптичність задається медіанним значенням.

$$\begin{array}{c} {(\frac{a_{2}}{a_{1}})_{m} = \tan(15^{\circ})} \nonumber \end{array}$$

Такий результат можна отримати дуже просто. Припустимо, що всі представницькі точки сфери Пуанкаре е однаково вірогідні. Враховуйте кількість:

$$\begin{array}{c} {S = \frac{2a_{1}a_{2}}{a_{1}^{2}+a_{2}^{2}}} \nonumber \end{array}$$

для довільної точки на сфері.

Візьміть середнє значення$|S|$ над сферою Пуанкаре, використовуючи статистичне припущення вище.

Вивести значення

$$\begin{array}{c} {(\frac{a_{2}}{a_{1}})_{0}} \nonumber \end{array}$$

що відповідає$\langle |S| \rangle$.