1.1: Симетрія

Last updated
Save as PDF

Page ID: 63441

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Групи виникають у природі, коли ми можемо знайти симетрію. Наприклад, людське тіло має бічну симетрію: якщо ви уявляєте собі поворот вліво і вправо, більшість людей виглядали б більш-менш однаково. (Насправді ми бачимо приклад цього кожного разу, коли дивимося в дзеркало.)

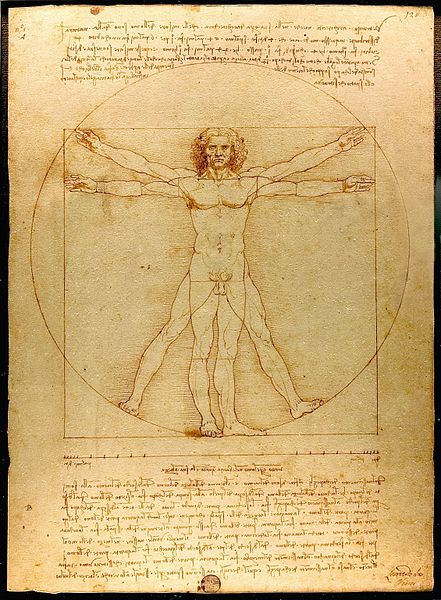
$Da_Vinci_Vitruve_Luc_Viatour.jpg$

Малюнок 1: Знаменитий ескіз Да Вінчі демонструє бічну симетрію в тілі людини. (Джерело)

Інший приклад - в утворенні кристалів. У кристалі атомна структура влаштовується в дуже симетричний візерунок, який можна побачити навіть неозброєним оком. Симетрія атомної структури означає, що атоми упаковані дуже регулярно, що призводить до приємних форм, які ми бачимо. Наприкінці 1800-х років математики використовували теорію груп, щоб класифікувати всі форми кристалів, які коли-небудь могли існувати у світі.

$pyrite.jpg$

Малюнок 2: Твін кристал піриту. (Джерело)

Візерунки плитки — двовимірні малюнки, які повторюються регулярними способами — також є прикладом симетрії. Багато культур досліджували симетрію за допомогою моделей укладання плитки, хоча вивчення плитки було особливо вишукано в ісламських культурах в середні віки. Заборони на зображення людських форм привели ісламських художників до дуже глибоких досліджень абстрактних дизайнів, з сильним акцентом на плитці. Теорія груп також може класифікувати всі можливі регулярні візерунки плитки, також відомі як тесселяції, що дозволяє нам перевірити, що всі можливі візерунки плитки були насправді виявлені ісламськими художниками! Є багато, багато цікавих візерунків плитки там: ось місце, щоб почати читати про них, якщо вам цікаво.

$Semi-regular-floor-3464.JPG$

Малюнок 3: Візерунки плитки демонструють цікаві симетрії! (Джерело)

Дуже глибокий приклад симетрії зустрічається в наших найбільш фундаментальних припущеннях у фізиці. Основний принцип стверджує, що важливим у фізичній системі є взаємозв'язок між усіма об'єктами, а не їх абсолютне положення. Цей принцип дозволяє сказати, що фізика, яку ми з'ясуємо на Землі, повинна працювати однаково і на Марсі. (До цих пір в історії світу це було дуже корисним припущенням.) Отже, якщо ви рухаєте всю систему в будь-якому напрямку (або обертаєте її або відбиваєте), система не «помітить». Ця інваріантність теж є своєрідною симетрією. Оскільки ви можете переміщати фізичну систему на будь-яку суму, не змінюючи її, фізична система має нескінченну кількість симетрій!

Так що ж таке група? Як ми можемо створити математику, щоб охопити вивчення симетрії? Це те, що ми розглянемо в цьому розділі.