Skip to main content
LibreTexts - Ukrayinska

5.3.11: Теорема ДемоІвра

  1. Last updated
  2. Save as PDF
  • Page ID
    54891

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Спростити обчислення ступенів комплексних чисел.

    Повноваження та коріння комплексних чисел

    Вручну обчислення (спрощення) такого твердження, як:\((14−17i)^5\) або\(\sqrt[4]{(3−2i)}\) в теперішній (прямокутній) формі, було б дуже інтенсивним процесом у кращому випадку.

    На щастя, ви дізнаєтеся на цьому уроці, що є альтернатива: теорема Де Муавра. Теорема Де Муавра дійсно є єдиним практичним методом знаходження степенів або коренів комплексного числа, але є підступ...

    Що потрібно зробити з комплексним числом, перш ніж теорема Де Муавра може бути використана?

    Повноваження та коріння комплексних чисел

    Повноваження комплексних чисел

    Як ми піднімаємо комплексне число до степеня? Почнемо з прикладу:

    \((−4−4i)^3=(−4−4i)\cdot (−4−4i)\cdot (−4−4i)\)

    У прямокутній формі це може вийти дуже складним. А як щодо\(r \; cis \; \theta\) форми?

    \((−4−4i)=4\sqrt{2} \; cis \; \left(\dfrac{5 \pi}{4}\right)\)

    Таким чином, проблема стає

    \(4\sqrt{2} \; cis \;\left(\dfrac{5 \pi}{4}\right)\cdot 4\sqrt{2} \; cis \;\left(\dfrac{5\pi}{4}\right)\cdot 4\sqrt{2} \; cis \;\left(\dfrac{5 \pi}{4}\right)\)

    і використовуючи наше правило множення з попереднього розділу,

    \((−4−4i)^3=(4\sqrt{2} )^3 \; cis \;(\dfrac{15\pi}{4})\)

    Зауважте,\((a + bi)^3= r^3 \; cis \; 3 \theta\)

    У словах: Підніміть r -значення до того ж ступеня, що і комплексне число піднімається, а потім\(\; cis \;\) помножте його на кут, помножений на число градуса.

    Розмірковуючи над прикладом вище, ми можемо виділити теорему Де Муавра:

    \(z = r(\cos \theta + i \sin \theta )\)Дозволяти складне число за\(r\; cis \;\theta\) формою. Якщо n є натуральним числом,\(z^n\) дорівнює\(z^n = r (\cos (n\theta ) + i \sin (n\theta ))\)

    Повинно бути зрозуміло, що полярна форма забезпечує набагато швидший результат для підняття комплексного числа до степені, ніж виконання завдання в прямокутній формі.

    Коріння комплексних чисел

    Ви, напевно, давно помітили, що коли нова операція представлена в математиці, часто слід зворотна операція. Це, як правило, тому, що зворотна операція часто процедурно схожа, і має сенс вивчати обидва одночасно.

    Це не виняток:

    Зворотна операція знаходження потужності для числа полягає в пошуку кореня того ж числа.

    1. Нагадаємо з алгебри, що будь-який корінь можна записати як\(x^{1/n}\)
    2. З огляду на, що формула теореми Де Муавра працює і для дробових ступенів, ту ж формулу можна використовувати для знаходження коренів:

    \(z ^{1/n}=(a+bi)^{1/n}=r^{1/n} \; cis \;\left(\dfrac{\theta }{n}\right)\)

    Приклад\(\PageIndex{1}\)

    Раніше вас запитали, що потрібно зробити з комплексним числом, перш ніж ви зможете використовувати теорему Де Муавра про нього.

    Рішення

    Операція з комплексним числом, записана в прямокутній формі, наприклад:\((13−4i)^3\) повинна бути перетворена в полярну форму перед використанням теореми Де Муавра.

    Приклад\(\PageIndex{2}\)

    Знайдіть значення\((1+\sqrt{3} i)^4\).

    Рішення

    \(r=\sqrt{(1)^2+(\sqrt{3} )^2}=2\)

    \(\tan \theta_{ref} =\dfrac{\sqrt{3} }{1}\),

    і\(\theta \) знаходиться в 1-му квадранті, так

    \(\theta =\dfrac{\pi}{3}\)

    Використовуючи наше рівняння зверху:

    \(\begin{aligned} z^4 &=r^4 \; cis \; 4\theta \\ z^4 &=(2)^4 \; cis \; \dfrac{4 \pi}{3} \end{aligned}\)

    Розширюється\(\; cis \;\) форма:

    \(\begin{aligned} z^4 &=16\left(\cos \left(\dfrac{4 \pi}{3}\right)+i \sin \left(\dfrac{4 \pi}{3}\right)\right) \\ &= 16((−0.5)−0.866i)\end{aligned}\)

    Нарешті у нас є

    \(z^4 = -8 - 13.856i\)

    Приклад\(\PageIndex{3}\)

    Знайти\(\sqrt{1+i}\).

    Рішення

    По-перше, рерайт в експоненціальному вигляді:\((1 + i)^{1/2}\)

    А тепер в полярному вигляді:

    \(\sqrt{1+i}=\left(\sqrt{2} \; cis \; \left(\dfrac{\pi}{4}\right)\right)^{1/2}\)

    Розширюється\(\; cis \;\) форма,

    \(=\left(\sqrt{2} \left(\cos \left(\dfrac{\pi}{4}\right)+i \sin \left(\dfrac{\pi}{4}\right)\right)\right)^{1/2}\)

    Використовуючи формулу:

    \(\begin{aligned}&=(2^{1/2})^{1/2}\left(\cos \left(\dfrac{1}{2} \cdot \dfrac{\pi }{4}\right)+i \sin \left(\dfrac{1}{2}\cdot \dfrac{\pi }{4}\right)\right) \\ &=2^{1/4}\left(\cos \left(\dfrac{\pi}{8} \right)+i \sin \left(\dfrac{\pi}{8} \right)\right)\end{aligned}\)

    У десятковій формі отримуємо

    \(\begin{aligned} &=1.189( 0.924 + 0.383i) \\ &=1.099 + 0.455i\end{aligned}\)

    Для перевірки помножимо результат на себе в прямокутному вигляді:

    \(\begin{aligned} (1.099+0.455i) \cdot (1.099+0.455i) &=1.0992+1.099(0.455i)+1.099(0.455i) + (0.455i)^2 \\ &=1.208+0.500i+0.500i+0.208i^2 \\ &=1.208+i−0.208 \text{ or } \\ &=1+i \end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Знайдіть значення\(x\):\(x_3=(1−\sqrt{3} i)\).

    Рішення

    Спочатку ставимо\(1−\sqrt{3} i\) в полярному вигляді.

    Використовувати\(x=1\),\(y=−\sqrt{3} \) щоб отримати\(r=2\),\(\theta =5\dfrac{\pi}{3}\)

    \(\begin{aligned} \text{let } z&=(1−\sqrt{3} i) && \text{in rectangular form} \\ z&=2 \; cis \; \left(5\dfrac{\pi}{3}\right) && \text{in polar form }\\ x&=(1−\sqrt{3} i)^{1/3} \\ x&=\left[2\; cis \; \left(\dfrac{5\pi}{3}\right)\right]^{1/3}\end{aligned}\)

    Скористайтеся теоремою Де Муйвра, щоб знайти перший розв'язок:

    \(x_1=2^{1/3}\; cis \; \left(\dfrac{5\pi /3}{3}\right)\)або\(2^{1/3}\; cis \;\left(\dfrac{5 \pi}{9}\right)\)

    Залиште відповідь у\(\; cis \;\) формі, щоб знайти решту рішень:

    \(n = 3\)що означає, що рішення 3\(\dfrac{2 \pi}{3}\) радіани один від одного або

    \(x_2=2^{1/3}\; cis \; \left(\dfrac{5 \pi}{9}+\dfrac{2 \pi}{3}\right)\)і\(x_3=2^{1/3}\; cis \; \left(\dfrac{5 \pi}{9}+\dfrac{2 \pi}{3}+\dfrac{2 \pi}{3}\right)\)

    ПРИМІТКА: Не потрібно додавати\(\dfrac{2 \pi}{3}\) знову. Додавання\(\dfrac{2 \pi}{3}\) тричі дорівнює\(2\pi \). Це призведе до обертання навколо повного кола і початку, де все почалося - це перше рішення.

    Три рішення:

    \(\begin{aligned} x_1&=2^{1/3}\; cis \;\left(\dfrac{5 \pi}{9}\right) \\ x_2&=2^{1/3}\; cis \; \left(\dfrac{11 \pi}{9}\right) \\ x_3&=2^{1/3}\; cis \; \left(\dfrac{17\pi}{ 9}\right) \end{aligned}\)

    Кожне з цих рішень при графіку буде\(\dfrac{2 \pi}{3}\) розділено.

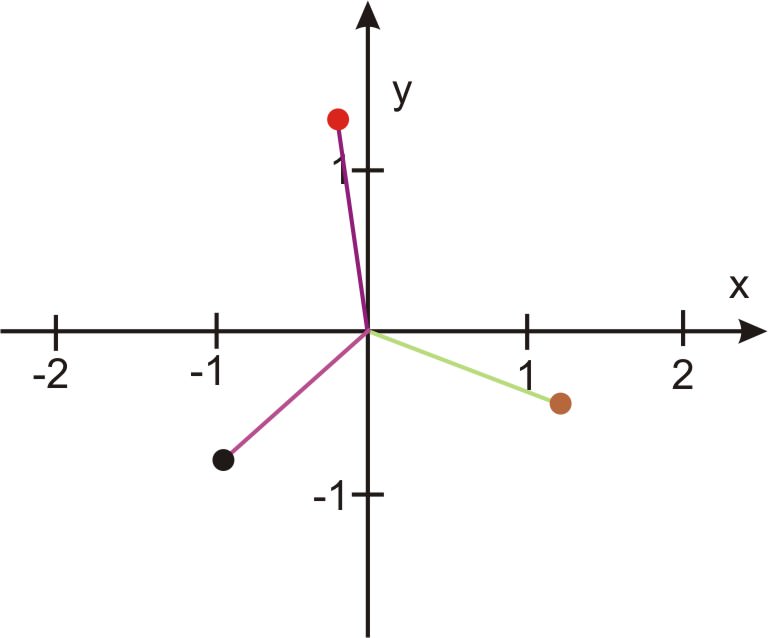
    F-D_2cda8a19e936092 ЕС97КБС5279 АЦД 0А1730д9С385302А0А1А7АФ +зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{1}\)

    Перевірте будь-яке з цих рішень, щоб перевірити, чи підтверджені результати.

    Перевірка другого рішення:

    \(\begin{aligned} x_2&=2^{1/3}\; cis \;(\dfrac{11 \pi}{9}) \\ &=1.260\left[\cos \left(\dfrac{11 \pi}{9}\right)+i \sin \left(\dfrac{11 \pi}{9}\right) \right] \\&=1.260[−0.766−0.643i] \\ &=−0.965−0.810i \end{aligned}\)

    Чи є\((-0.965 – 0.810i)^3\) чи\((-0.965 – 0.810i) (-0.965 – 0.810i) (-0.965 – 0.810i)\)

    \(=(1−\sqrt{3} i)\)?

    Приклад\(\PageIndex{5}\)

    Які два квадратних кореня\(i\)?

    Рішення

    Нехай\(z=\sqrt{0+i}\).

    \(\begin{aligned} z_1 &=\left[1\times \; cis \;\dfrac{\pi}{4}\right] &\quad \text{ or } \quad& z_2=\left[1\times \; cis \;5\dfrac{\pi}{4}\right] \\ z_1 &=1\left(\cos \dfrac{\pi}{4}+i \sin \dfrac{\pi}{4}\right) &\quad \text{ or } \quad& z_2=1\left(\cos 5\dfrac{\pi}{4}+i \sin 5\dfrac{\pi}{4}\right) \\ z_1 &=0.707+0.707i &\quad \text{or } \quad& z_2=−0.707−0.707i \end{aligned}\)

    Перевірте\(z_1 \) рішення:\((0.707 + 0.707i)^2 = i\)?

    \(0.500 + 0.500i + 0.500i + 0.500i^2= 0.500 + i + 0.500(-1)\)або\(i\)

    Приклад\(\PageIndex{6}\)

    Розрахувати\(\sqrt[4]{(1+0i)}\). Які чотири четверті корені 1?

    Рішення

    Нехай\(z = 1\) або\(z = 1 + 0i\). Тоді проблема стає знахідкою\(z^{1/4}= (1 + 0i)^{1/4}\).

    Так як\(r=1 \theta =0\),\(z^{1/4}=[1\times \; cis \; 0]^{1/4}\) з\(z_1 =1^{1/4} \left(\cos \dfrac{0}{4}+i \sin \dfrac{0}{4}\right)\) або\(1(1+0)\) або\(1\)

    Цей корінь не є несподіванкою. Тепер використовуйте De Moivre, щоб знайти інші корені:

    \(z_2=1^{1/4} \left[\cos \left(0+\dfrac{\pi}{2} \right)+i \sin \left(0+\dfrac{\pi}{2} \right) \right] \)

    Так як існує 4 кореня,\(2\pi\) діливши на 4 врожайності\(0.5\pi\)

    \(0 + i\)або просто\(i\)\(z_3=1^{1/4}\left[\cos \left(0+\dfrac{2 \pi}{2} \right)+i \sin \left(0+\dfrac{2 \pi}{2} \right) \right]\) яка врожайність\(z_3 = -1\)

    Нарешті,\(z_4=1^{1/4} \left[\cos \left(0+\dfrac{3 \pi}{2} \right)+i \sin \left(0+\dfrac{3 \pi}{2} \right)\right]\) або z_4 =−i

    Чотири четвертих кореня 1 - це 1, i, -1 і -i.

    Приклад\(\PageIndex{7}\)

    Розрахувати\((\sqrt{3} +i)^7\).

    Рішення

    Для обчислення\((\sqrt{3} +i)^7\) почніть з перетворення в\(r\; cis \; \) форму.

    Спочатку знайдіть\(r\). Нагадаємо\(r=\sqrt{\sqrt{3}^2 +1^2}\).

    \(\begin{aligned} r&=\sqrt{3+1} \\ r&=2 \end{aligned}\)

    Якщо\(\cos \theta =\dfrac{\sqrt{3}}{2} \) і\(\sin \theta =\dfrac{1}{2}\) тоді\(\theta =30^{\circ}\) і знаходиться в квадранті I. Тепер, коли ми маємо тригонометричну форму, все інше легко:

    \(\begin{aligned} (\sqrt{3} +i)^7&=[2(\cos 30^{\circ}+i\sin 30^{\circ})]^7 && \text{Write the original problem in } r \; cis \; \text{form} \\ &=2^7[(\cos (7\cdot 30^{\circ})+i\sin (7\cdot 30^{\circ})] && \text{De Moivre's theorem}\\ &=128 \left[−\dfrac{\sqrt{3} }{2}+\dfrac{−1}{2} i \right] && \text{Simplify} \\ (\sqrt{3} +i)^7&=−64\sqrt{3} −64i &&\text{Simplify again} \\ \therefore (\sqrt{3} +i)^7&=−64\sqrt{3} −64i \end{aligned}\)

    Рецензія

    Виконайте зазначену операцію над цими комплексними числами:

    1. Розділити:\(\dfrac{2+3i}{1−i}\)
    2. Помножити:\((−6−i)(−6+i)\)
    3. Помножити:\(\left(\dfrac{\sqrt{3}}{2}−\dfrac{1}{2} i\right)^2\)
    4. Знайдіть виріб, використовуючи полярну форму:\((2+2i)(\sqrt{3} −i)\)
    5. Помножити:\(2(\cos 40^{\circ} +i \sin 40^{\circ} )\cdot 4(\cos 20^{\circ} +i \sin 20^{\circ} )\)
    6. Помножити:\(2(\cos \dfrac{\pi}{8} +i \sin \dfrac{\pi}{8} )\cdot 2\left(\cos \dfrac{\pi}{10} +i \sin \dfrac{\pi}{10} \right)\)
    7. Розділити:\(2(\cos 80^{\circ} +i \sin 80^{\circ} )\div 6(\cos 200^{\circ} +i \sin 200^{\circ} )\)
    8. Розділити:\(3 \; cis \;(130^{\circ} )\div 4 \; cis \;(270^{\circ} )\)

    Використовуйте теорему Де Муйвра.

    1. \([3(\cos 80^{\circ} +i \sin 80^{\circ} )]^3\)
    2. \(\left[\sqrt{2} \left(\cos \dfrac{5\pi }{16}+i \sin \dfrac{5 \pi}{16} \right)\right]^4\)
    3. \((\sqrt{3} −i)^6\)
    4. Визначте 3 складних кубових коренів\(1+i\)
    5. Визначте 4 складних четвертих кореня\(−16i\)
    6. Визначте п'ять складних п'ятих коренів\(i\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.10.

    Лексика

    Термін Визначення
    комплексне число Комплексне число - це сума дійсного числа і уявного числа, записаного у вигляді\(a+bi\).
    Теорема Де Муівра Теорема Де Муавра є єдиним практичним ручним методом ідентифікації степенів або коренів комплексних чисел. Теорема стверджує,\(z=r(\cos \theta +i\sin \theta )\) що якщо комплексне число за\(r\; cis \;\theta \) формою, а n - натуральне, то\(z^n=r^n(\cos (n\theta )+i\sin (n\theta ))\).