2.2.4: Вирішіть правильні трикутники
- Page ID
- 54807
Використання обернених тригонометричних функцій для розв'язання відсутніх відомостей про правильні трикутники.
Обернені тригонометричні коефіцієнти
У математиці слово зворотне означає «скасувати». Наприклад, додавання та віднімання є оберненнями один одного, оскільки одне скасовує інше. Коли ми використовуємо зворотні тригонометричні коефіцієнти, ми можемо знайти гострі кутові міри до тих пір, поки нам дано дві сторони.
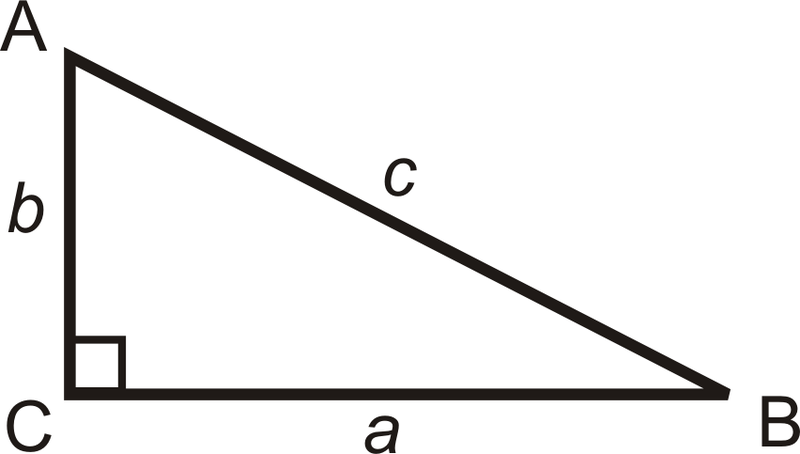
Зворотний тангенс: Позначений\(\tan ^{-1}\), «-1» означає зворотний.
\(\tan ^{-1} \left(\dfrac{b}{a}\right)=m\angle B\)і\(\tan ^{-1} \left(\dfrac{a}{b}\right)=m\angle A.\)
Зворотний синус: Позначений\(\sin ^{-1}\).
\(\sin ^{-1} \left(\dfrac{b}{c}\right)=m\angle B\)і\(\sin ^{-1} \left(\dfrac{a}{c}\right)=m\angle A.\)
Зворотний косинус: Позначений\(\cos ^{-1}\).
\(\cos ^{-1} \left(\dfrac{a}{c}\right)=m\angle B\)і\(\cos ^{-1} \left(\dfrac{b}{c}\right)=m\angle A.\)
У більшості проблем, щоб знайти міру кутів вам потрібно буде скористатися вашим калькулятором. На більшості наукових і графічних калькуляторів кнопки виглядають як\([\sin ^{-1}]\)\([\cos ^{-1}]\), і\([\(\tan ^{-1}]\). Можливо, вам також доведеться натиснути кнопку зсуву або другу кнопку, щоб отримати доступ до цих функцій.
Тепер, коли ви знаєте як коефіцієнти трига, так і зворотні коефіцієнти трига, ви можете вирішити прямокутний трикутник. Щоб вирішити прямокутний трикутник, потрібно знайти в ньому всі сторони і кути. Зазвичай ви використовуєте синус, косинус або тангенс; зворотний синус, обернений косинус або обернений тангенс; або теорему Піфагора.
Що робити, якщо вам сказали\(\angle Z\) тангенс 0.6494? Як ви могли знайти міру\(\angle Z\)?
Розв'яжіть прямокутний трикутник.
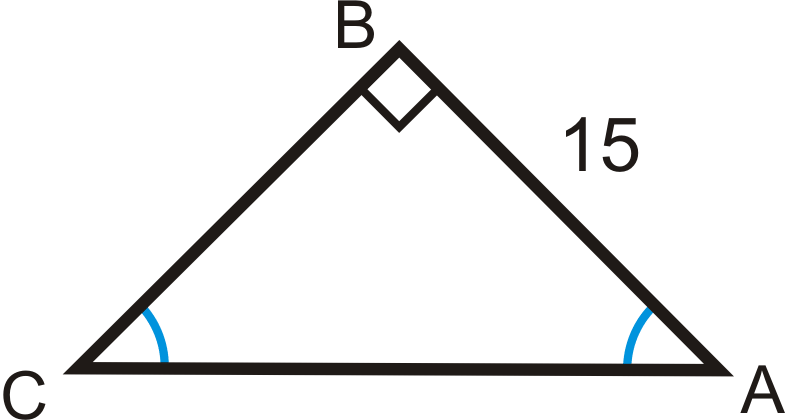
Рішення
Два гострі кути є конгруентними, що робить їх обидва\(45^{\circ}\). Це трикутник 45-45-90. Ви можете використовувати тригонометричні співвідношення або спеціальні співвідношення прямокутного трикутника.
Тригонометричні коефіцієнти
\ (\ почати {масив} {rlrl}
\ tan 45^ {\ circ} & =\ dfrac {15} {B C} &\ sin 45^ {\ circ} & =\ dfrac {15} {\
dfrac}} =15 & A C & =\ dfrac {15} {\ tan 45^ {\ circ}} =15 & A C & =\ dfrac {15} {\ sin 45^ {\ circ}}\ приблизно 21.21
\ кінець {масив}\)
Коефіцієнти трикутника 45-45-90
\(BC=AB=15 \text{, } AC=15\sqrt{2} \approx 21.21\)
Використовуйте сторони трикутника і ваш калькулятор, щоб знайти значення\(\angle A\). Округлите відповідь до найближчої десятої частки градуса.
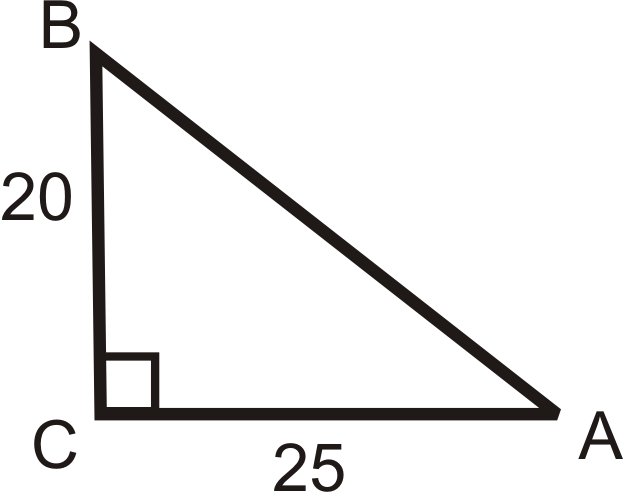
Рішення
Відносно до\(\angle A\), нам дають протилежну ногу і прилеглу ногу. Це означає, що ми повинні використовувати дотичне співвідношення.
\(\tan A=\dfrac{20}{25}=\dfrac{4}{5}\). Отже,\(\tan ^{-1} \dfrac{4}{5}=m\angle A\). Тепер скористайтеся калькулятором.
Якщо ви використовуєте TI-83 або 84, натискання клавіш буде: [2nd] [TAN] (\(\dfrac{4}{5}\)) [ENTER] і екран виглядає так:

\(m\angle A \approx 38.7^{\circ}\)
\(\angle A\)- гострий кут в прямокутному трикутнику. Знайдіть\(m\angle A\) до найближчої десятої градуса для\(\sin A=0.68\)\(\cos A=0.85\), і\(\tan A=0.34\).
Рішення
\(\begin{aligned} m\angle A&=\sin ^{-1} 0.68\approx 42.8^{\circ} \\ m\angle A&=\cos ^{-1} 0.85\approx 31.8^{\circ} \\ m\angle A&=\tan ^{-1} 0.34\approx 18.8^{\circ} \end{aligned}\)
Розв'яжіть прямокутний трикутник.
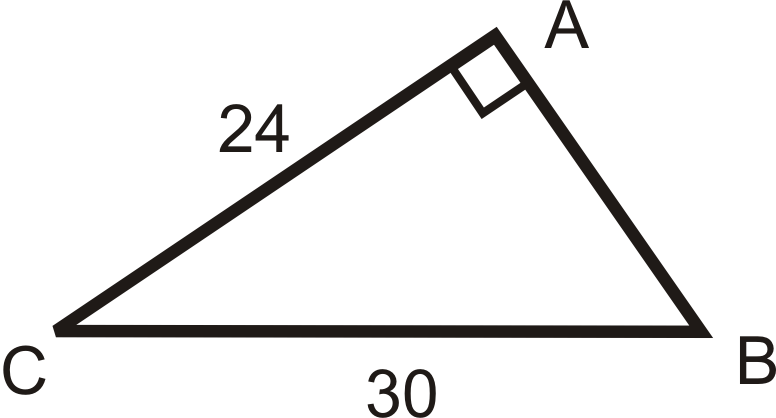
Рішення
Щоб вирішити цей прямокутний трикутник, нам потрібно знайти\(AB\),\(m\angle C\) і\(m\angle B\). Використовуйте тільки ті значення, які вам задані.
\(\underline{AB}: \text{ Use the Pythagorean Theorem.}\)
\(\begin{aligned} 24^2+AB^2&=30^2 \\ 576+AB^2&=900 \\ AB^2&=324 \\ AB&=\sqrt{324}=18 \end{aligned}\)
\(\underline{m\angle B} : \text{ Use the inverse sine ratio.}\)
\(\begin{aligned} \sin B &=\dfrac{24}{30}=\dfrac{4}{5} \\ \sin ^{-1} (45) &\approx 53.1^{\circ} =m\angle B\end{aligned}\)
\(\underline{m\angle C} : \text{ Use the inverse cosine ratio.}\)
\(\cos C=\dfrac{24}{30}=\dfrac{4}{5} \rightarrow \cos ^{-1} (\dfrac{4}{5})\approx 36.9^{\circ} =m\angle C\)
Коли б ви використовували гріх і коли б ви використовували\(\sin ^{-1}\)?
Рішення
Ви б використали гріх, коли вам дають кут, і ви вирішуєте для відсутньої сторони. Ви б використовувати,\(\sin ^{-1} \) коли вам даються сторони, і ви вирішуєте для відсутнього кута.
Рецензія
Скористайтеся калькулятором\(m\angle A\), щоб знайти до найближчої десятої градуса.
-
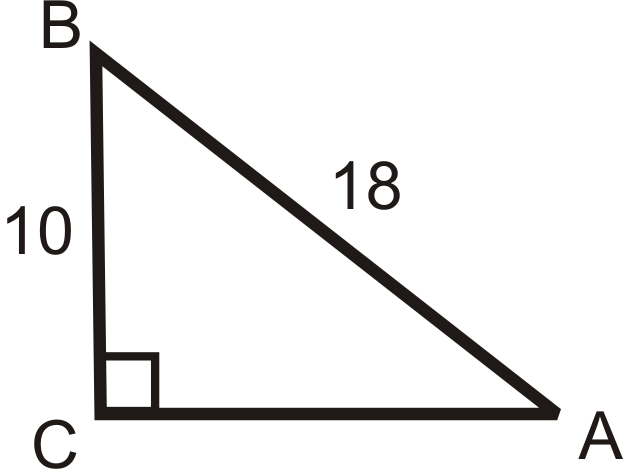
Малюнок\(\PageIndex{6}\) -
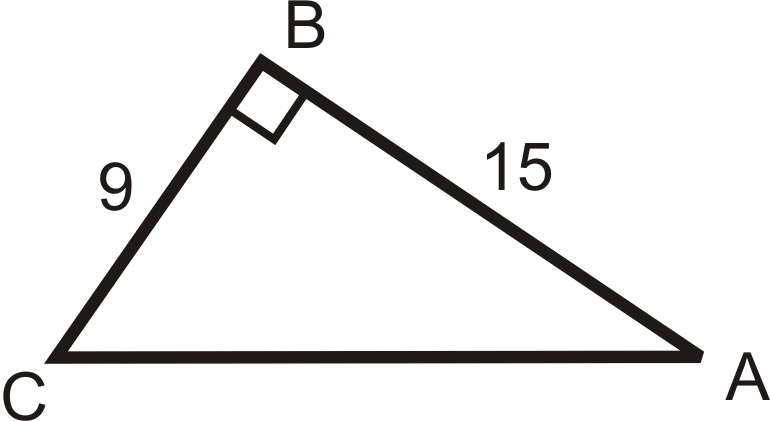
Малюнок\(\PageIndex{7}\) -
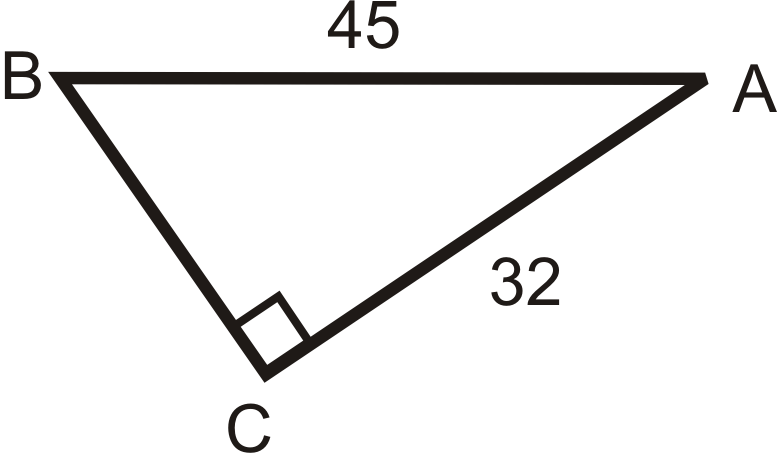
Малюнок\(\PageIndex{8}\) -
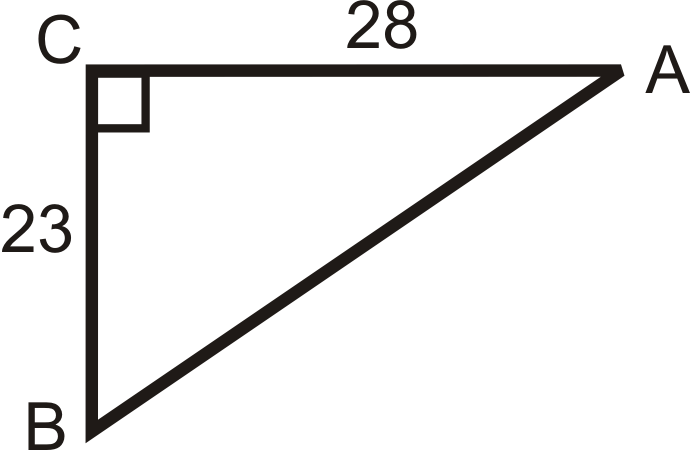
Малюнок\(\PageIndex{9}\) -
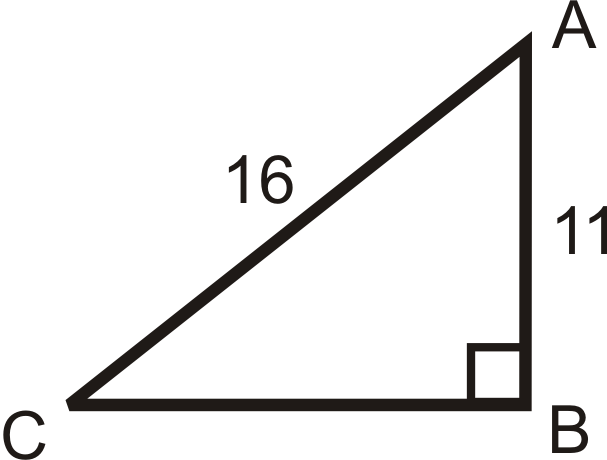
Малюнок\(\PageIndex{10}\) -
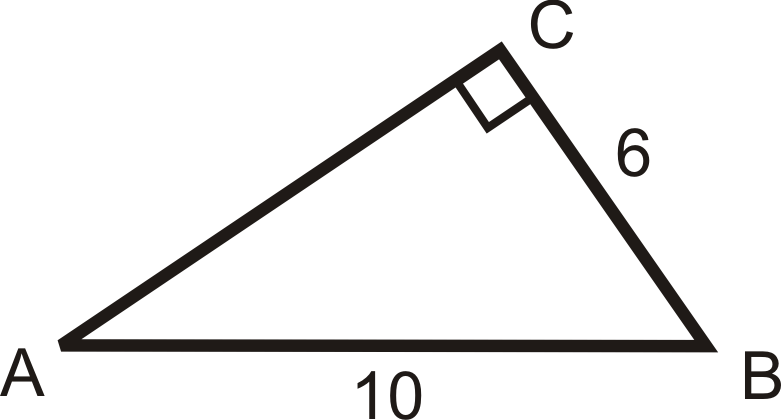
Малюнок\(\PageIndex{11}\)
\(\angle A\)Дозволяти бути гострим кутом в прямокутний трикутник. Знайдіть\(m\angle A\) до найближчої десятої градуса.
- \(\sin A=0.5684\)
- \(\cos A=0.1234\)
- \(\tan A=2.78\)
- \(\cos ^{-1} 0.9845\)
- \(\tan ^{-1} 15.93\)
- \(\sin ^{-1} 0.7851\)
Розв'язування наступних правильних трикутників. Знайти всі відсутні сторони і кути. Округляйте будь-які десяткові відповіді до найближчої десятої.
-
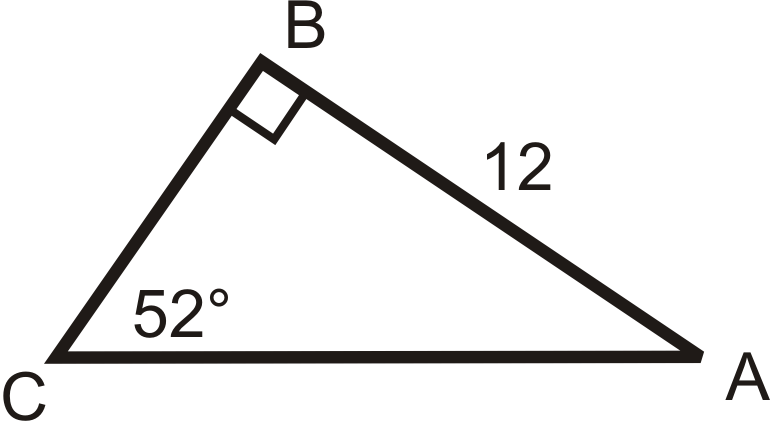
Малюнок\(\PageIndex{12}\) -
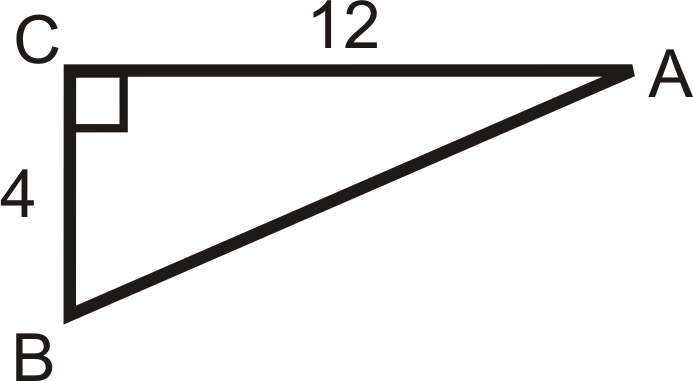
Малюнок\(\PageIndex{13}\) -
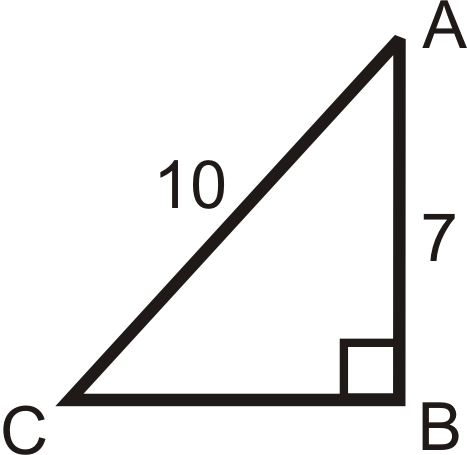
Малюнок\(\PageIndex{14}\) -
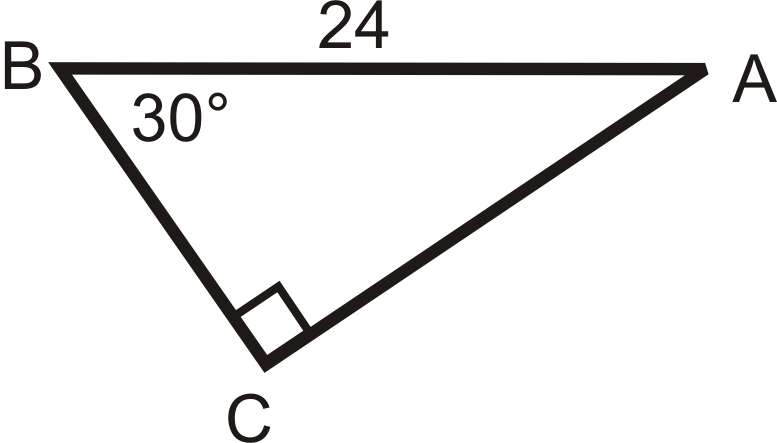
Малюнок\(\PageIndex{15}\) -
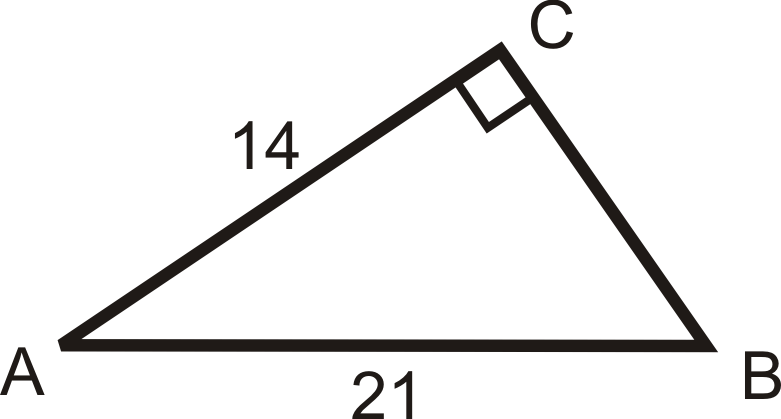
Малюнок\(\PageIndex{16}\) -
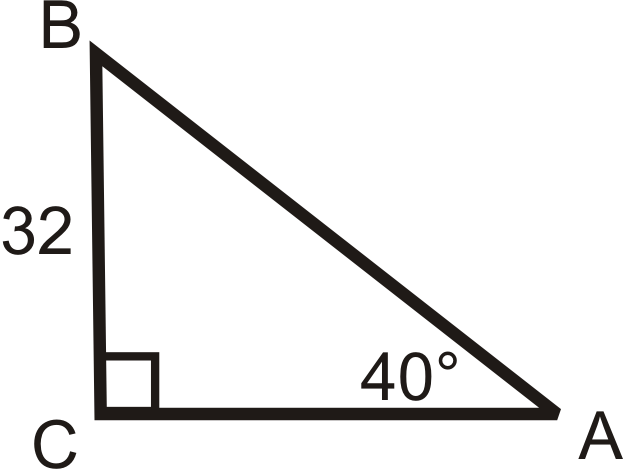
Малюнок\(\PageIndex{17}\) -
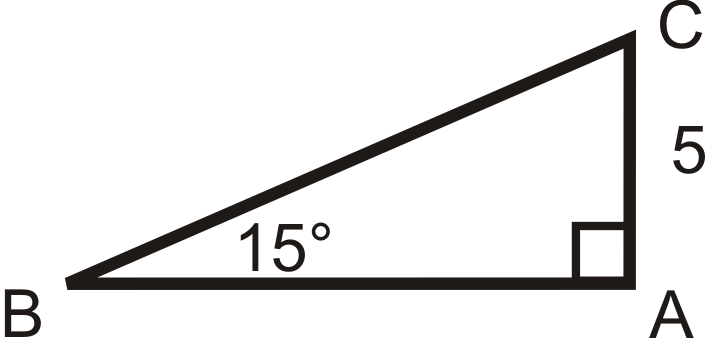
Малюнок\(\PageIndex{18}\) -
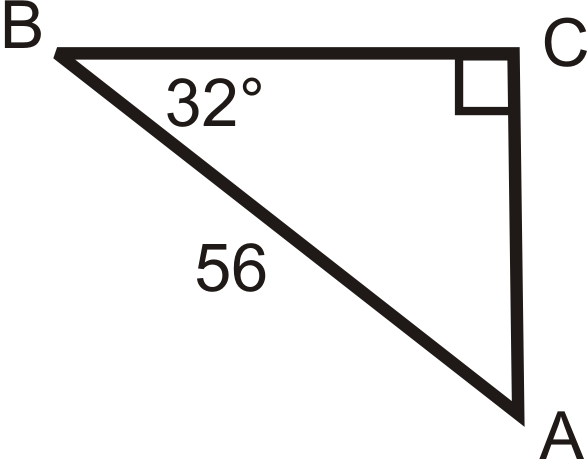
Малюнок\(\PageIndex{19}\) -
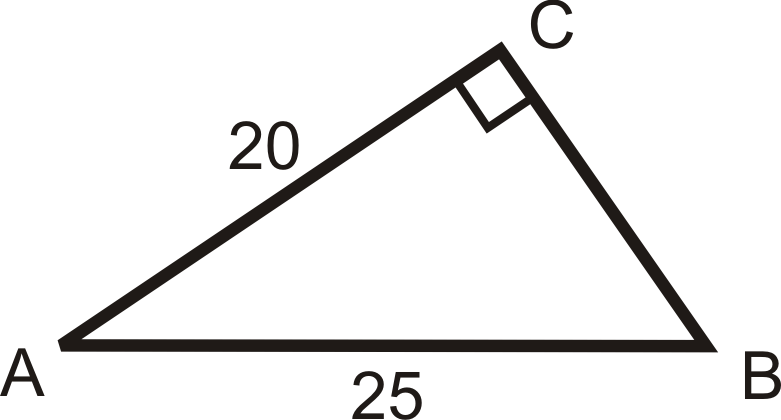
Малюнок\(\PageIndex{20}\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.10.
Додаткові ресурси
Відео: Вступ до зворотних тригонометричних функцій
Діяльність: Зворотні тригонометричні коефіцієнти Питання обговорення
Навчальні посібники: Посібник з вивчення тригонометричних коефіцієнтів
Практика: Розв'язуйте правильні трикутники