2.2.2: Додатки функцій Trig
- Page ID
- 54816
Використовуйте калькулятор, щоб знайти синус, косинус і тангенс у базових додатках
Моделювання періодичної поведінки
Цей урок вивчить, як реальні приклади періодичної поведінки можуть бути змодельовані за допомогою тригонометричних функцій. Іншими словами, предмети, які перебувають у русі - такі як поворот колеса або переміщення хвиль - можна змоделювати та розуміти за допомогою тригонометрії.
Розминка
Тригонометричні функції, такі як синус і косинус, відображають періодичну поведінку при графіку. Використовуйте інтерактивні нижче, щоб побачити періодичну поведінку синусоїдальної функції. Пізніше в цьому розділі ви побачите, як реальні проблеми можуть бути змодельовані та вирішені за допомогою функцій, подібних до цих.
Додайте тут інтерактивний текст елемента. Це поле НЕ буде друкувати в PDF-файлах
Опрацюйте це 1
Двоє студентів, Менні та Джуліса, вели дискусію про те, як моделювати довжину хвилі частоти радіостанції своєї школи. Щоб спростити їх дебати, вони використовували іншу модель хвилі, як показано нижче.
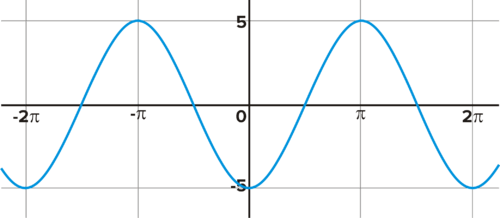
Менні каже, що рівняння для наведеного вище графіка є,\(f(x)=5 \sin\left(x−\dfrac{\pi}{2}\right)\) і Юліса каже, що це так\(f(x)=5 \cos x\).
- Без графіка рівнянь, ви можете сказати, який студент є правильним, і якщо так, то хто?
- Звідки ти знаєш?
- Як виглядатиме графік неправильного рівняння у порівнянні з графіком вище?
Обговорення
Нагадаємо, що рівняння для косинусної функції - це\(y=A\cos(w(x−h))+k\) де\(A\) змінюється амплітуда (відстань між середньою точкою та піком або долиною графіка), h змінює початок фази (рух графіка вліво і вправо по осях),\(k\) змінює середню лінію, а w змінює період від базової функції, яка виникає між 0 і\(2\pi\). Ми можемо сказати, що цей графік має амплітуду + 5, а період 1.
Але це косинусна функція, як вважає Юліса, або синусова функція зі зміщенням фази, як вважає Менні? Якщо ви графуєте ці дві функції, а також\(y=5 \sin x\) ви побачите тонкі, але важливі відмінності між трьома графіками.
Працюйте це 2
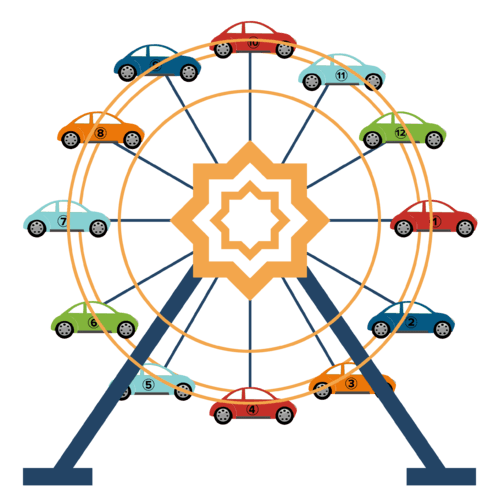
Велике колесо огляду має діаметр 100 футів і має 12 легкових автомобілів. Колесо огляду обертається проти годинникової стрілки і займає 1 хвилину, щоб завершити повне обертання. Вершники піднімаються по сходах, щоб сісти з платформи, яка знаходиться на висоті 60 футів над землею, і горизонтальна до центру колеса огляду. У цьому випадку висота автомобіля - це відстань між автомобілем і платформою (не висота автомобіля від землі). Ко-висота - це горизонтальна відстань між автомобілем і вертикальною лінією, яка проходить вгору і вниз через центр колеса огляду. Іншими словами, якщо автомобіль знаходився за\((x,y)\) координатою, спів-висота є,\(x\) а висота є\(y\).
- \(\theta =0\)Дозволяти представляти позицію автомобіля 1 у сценарії вище. Намалюйте графіки висоти і со-висоти автомобіля 1 як функції\(\theta\), кількості радіанів, через які автомобіль обертався.
- Яка амплітуда функцій висоти та співвисоти для колеса огляду?
- Якщо\(X(\theta)\) представляє со-висоту і\(Y(\theta)\) представляє висоту автомобіля, які тригонометричні функції представлятимуть спів-висоту та висоту з точки зору\(\theta\)?
Обговорення
Щоб визначити висоту автомобіля 1, коли колесо огляду обертається, врахуйте, що через 15 секунд (що відбувається\(\dfrac{1}{4}\) навколо або\(\dfrac{\pi}{2}\) радіани), автомобіль знаходиться у верхній частині колеса, яке, як ми знаємо, знаходиться на 50 футів над платформою. Наскільки високо буде автомобіль через 15 секунд після цього? Після всього 45 секунд? Після 1 хвилини обертання?
На графіку нижче представлена со-висота автомобіля. За 0 секунд автомобіль знаходиться на відстані 50 футів від центру колеса. Коли автомобіль знаходиться в\(\pi\) радіанах, як далеко він буде від вертикальної лінії, яка проходить через центр колеса огляду? Чому деякі значення ко-висоти нижче від'ємних чисел?
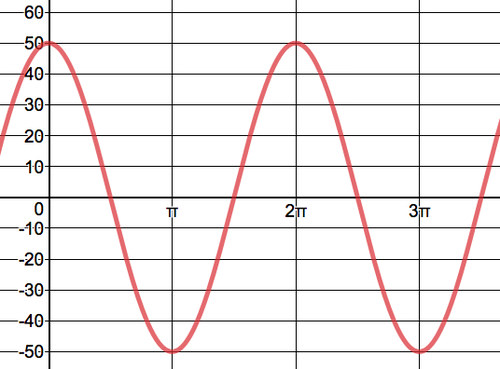
Амплітуда функції ко-висоти становить 50, оскільки автомобіль буде коливатися від +50 до -50 футів від вертикальної лінії (як\(y\) -вісь), що проходить через центр колеса огляду. Тому co-height може бути представлений функцією\(f(\theta )=50 \cos(\theta)\).
Не забувайте: вам все одно потрібно створити графік і знайти функцію для висоти автомобіля 1.
Використовуючи сценарій колеса огляду зверху, як би ви представляли висоту автомобіля як відстань від землі? Як би вплинути на спільну висоту, вимірюючи висоту від землі, а не з платформи? Як виглядатимуть графіки висоти та висоти?
Рішення
Ко-висота не зміниться, оскільки горизонтальна відстань між автомобілем та вертикальною лінією через центр колеса огляду не буде впливати на висоту платформи або положення автомобіля 1, коли гонщики сідають.
У цьому прикладі, оскільки ви вимірюєте висоту автомобіля 1 від землі, найвища точка, яку автомобіль досягає, становитиме 50 футів (радіус колеса) плюс 60 футів (висота платформи), або 110 футів. Найнижча точка, до якої досягає автомобіль, буде -50 футів (нижче центру колеса) плюс 60 футів (висота платформи), або 10 футів від землі. Графік висоти в залежності від кількості обертань знаходиться нижче.
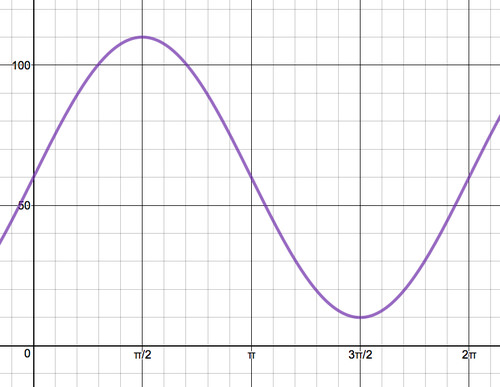
Вище наведено графік функції\(Y(\theta )=50 \sin \theta +60\).
Колесо огляду має висоту 40 футів. Існує 25-футова платформа, щоб потрапити в перший автомобіль, який завантажує знизу колеса (не збоку, як у попередніх прикладах). Додатково колесо огляду обертається проти годинникової стрілки, здійснюючи одне повне обертання кожні 2 хвилини. Напишіть та графікуйте функції для висоти (від землі) та спів-висоти колеса огляду за часом (у хвилинах).
Рішення
Нехай t = час. Почніть з визначення значень для A, w, h і k як для висоти, так і для со-висоти.
Зі висотою:
- Колесо має діаметр 40 футів, тому воно матиме максимальну та мінімальну висоту 20 футів та -20 футів відповідно до середньої лінії. Тому амплітуда (A) =20.
- Колесо обертається раз в 2 хвилини. Оскільки пасажири бортують знизу, що є обертанням за годинниковою стрілкою -14 від осі x, колесо огляду повинно обертатися +14 проти годинникової стрілки, щоб висота була на максимумі +20 футів. Ця чверть обертання займає 12 хвилин, а тому значення h (зсув фаз) дорівнює 12.
- Через 1 хвилину колесо огляду зробило обертання\ pi. Тому період (w) =\ pi.
- На со-висоту не впливає розташування центру колеса. Тому k=0.
- Рівняння для со-висоти таке:\(X(t)=20 \cos(\pi (x−\dfrac{1}{2}))\).
Висота:
- Щоб визначити висоту Автомобіля 1 від землі, потрібно буде підлаштуватися під висоту платформи. Платформа додає 25 футів до дна колеса огляду, що робить центр 20 футів+25 футів (або 45 футів) над землею. Це означає, що висота автомобіля 1, по відношенню до землі, становить 25 футів у найнижчій точці і 65 у найвищій точці, з k = 45.
- Рівняння для висоти таке:\(Y(t)=20 \sin(\pi (x−\dfrac{1}{2}))+45\).
Графік висоти в залежності від часу, при цьому Автомобіль 1 починається в нижній частині колеса і обертається за годинниковою стрілкою, виглядає так:
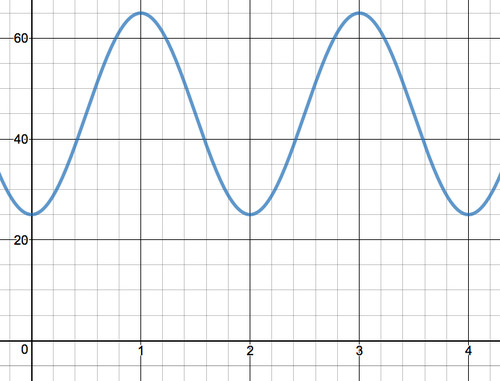
Додайте тут інтерактивний текст елемента. Це поле НЕ буде друкувати в PDF-файлах
Це відео демонструє, як вирішити подібну проблему колеса огляду.
Працюйте це 3
Ви з двома друзями їдете на колесі огляду в прикладі 2. Ви знаходитесь в автомобілі 1, інший друг знаходиться в автомобілі 3, а третій друг знаходиться в автомобілі 5. Коли ви дійдете до верхньої частини колеса, ви дивитеся вниз, щоб побачити своїх друзів десь під вами. Наскільки вище ваш автомобіль, ніж Автомобіль 3 і Автомобіль 5?
Обговорення
Коли ви знаходитесь у верхній частині колеса, наскільки високо ви будете? І скільки обороту, в радіанах, ви зробите? Розглянемо, де інші автомобілі знаходяться в колі; іншими словами, скільки повороту (знову ж таки в радіанах) зробили Автомобілі 3 і 5?
З огляду на амплітуду (20 футів) і висоту платформи (25 футів), ваш зріст буде 45 футів у верхній частині колеса, що є\(\pi\) радіанами від стартового місця. У цей момент, припустимо, ваш друг в автомобілі 3 повернувся\(120^{\circ}\) з місця старту, що становить 13 повного повороту. Як ви використовуєте цю інформацію та рівняння висоти колеса огляду для визначення висоти автомобіля 3?
Оскільки вам потрібно лише виміряти висоту автомобілів, швидкість колеса огляду не включається в рівняння, яке змінює значення w Додатково змініть вимір повороту в радіани. Яким буде рівняння без w?
У вас повинні вийти:\(Y(t)=20 \sin\left(x−\dfrac{\pi}{2}\right)+45\). Далі підключаємо частину повороту автомобіля 3 зробила (в радіанах) і вирішуємо:
\(\begin{aligned} X(t)&=20 \sin \left(\dfrac{2\pi}{3}−\dfrac{\pi}{2}\right)+45 \\ X(t)&=20 \sin\left(\dfrac{\pi}{6}\right)+45 \\ X(t)&=55\end{aligned}\)
Це означає, що ви 65 футів - 55 футів = 10 футів вище, ніж ваш друг в автомобілі 3.
Наскільки ви вище, ніж ваш друг в автомобілі 5, якщо автомобілі розташовані рівномірно один від одного?
Що б змінилося в процесі вирішення цієї проблеми, якби замість 12 автомобілів було всього 8 автомобілів? А як щодо того, якби автомобілів було вдвічі більше?
Інші моделі періодичної поведінки
Цей урок моделював періодичну поведінку за допомогою обертання автомобіля навколо колеса огляду для вивчення зв'язків між перетвореними тригонометричними функціями та їх графіками на основі реальних життєвих сценаріїв. Однак обертові колеса огляду - далеко не єдині «справжні» речі, які можна моделювати за допомогою тригонометричних функцій або мають періодичну поведінку.
Наприклад, припливи і відливи можна моделювати і передбачити за допомогою періодичних функцій, оскільки вчені можуть визначити висоту води в різний час доби (коли рівень води низький, приплив низький). Звукові хвилі, артеріальний тиск та зміни температури також можуть бути змодельовані як періодичні функції.
CK-12 Інтерактивний
Рецензія
- Для наведених нижче графіків визначте значення амплітуди, періоду, частоти, зсуву фаз та середньої лінії. Потім запишіть рівняння для графіка.
-
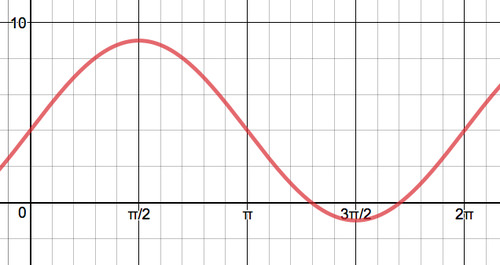
Малюнок\(\PageIndex{5}\) -
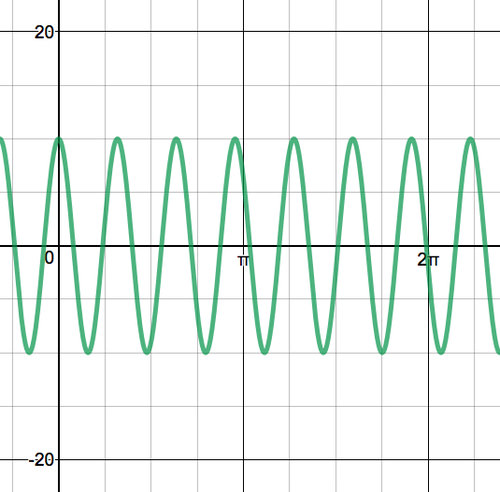
Малюнок\(\PageIndex{6}\) -
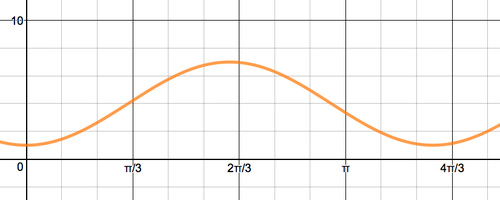
Малюнок\(\PageIndex{7}\)
-
- Поїздка Anansi the Spider - це невелике колесо огляду в дитячому парку розваг. Є 8 автомобілів на їзді, розставлені кожен\(45^{\circ}\). Колесо огляду знаходиться на 16 футах зверху вниз, і діти завантажуються в Автомобіль 1 знизу на платформі, яка знаходиться в 4 футах від землі. Поїздка займає 1 хвилину для повного обертання.
- Намалюйте функцію для висоти автомобіля 1 щодо часу, коли колесо огляду обертається протягом трьох хвилин.
- Знайдіть формулу для функції, яку ви намалювали вище.
- Визначте іншу функцію, яка матиме той самий графік, який ви намалювали в частині a.
- Ви стоїте на пірсі і вимірюєте висоту води під вами в різний час кожен день. О 3 годині вечора рівень води знаходиться на позначці 7 футів. До 9 вечора вода опустилася на 1 фут. А до 3 ранку рівень води знову піднімається на 7 футів.
- Намалюйте графік, враховуючи інформацію, яку ви маєте.
- Визначте амплітуду, фазовий зсув, період та середню лінію. [Підказка: Приплив займає 12 годин, щоб пройти повне обертання\(2\pi\), так що буде період, якщо ви вимірюєте в годинами?]
- Виведіть формулу, яка б моделювала висоту води, починаючи з 12 вечора першого дня, і яка показує висоту води протягом 24-годинного періоду.
- Графік формули за допомогою графічного калькулятора або програми, щоб підтвердити, що ваші відповіді на частини a-c є правильними.
- Якою буде висота води о 6 ранку?
- Зовнішня температура (у Фаренгейті) збиралася щогодини в холодний зимовий день протягом 24 годин. О 12 годині вечора температура була\(30^{\circ}\). До 6 вечора вона досягла\(50^{\circ}\), найтепліша зафіксована температура в період вимірювання. До 6 ранку температура опустилася до найнижчої точки\(10^{\circ}\).
- Намалюйте графік, враховуючи інформацію, яку ви маєте.
- Визначте амплітуду, фазовий зсув, період та середню лінію вашого графіка.
- Виведіть формулу, яка моделює температуру протягом 24-годинного періоду.