Skip to main content
LibreTexts - Ukrayinska

8.4.1: Площа під кривою

  1. Last updated
  2. Save as PDF
  • Page ID
    55043

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Площа під кривою

    Розрахунок площі під пряму можна проводити за допомогою геометрії. Розрахунок площі під кривою лінією вимагає обчислення. Часто площа під кривою може бути інтерпретована як накопичена кількість будь-якої функції моделювання. Припустимо, швидкість автомобіля в метрах в секунду може бути змодельована квадратичним за перші 8 секунд розгону:

    \(\ s(t)=t^{2}\)

    Як далеко автомобіль проїхав за 8 секунд?

    Пошук площі під кривою

    Площа під кривою може бути апроксимована прямокутниками, однаково розташованими під кривою, як показано нижче. Для узгодженості ви можете вибрати, чи повинні поля потрапляти на криву в лівому куті, правому куті, максимальному значенні або мінімальному значенні. Чим більше ящиків ви використовуєте, тим вужчими будуть коробки і, таким чином, тим точніше буде ваше наближення площі.

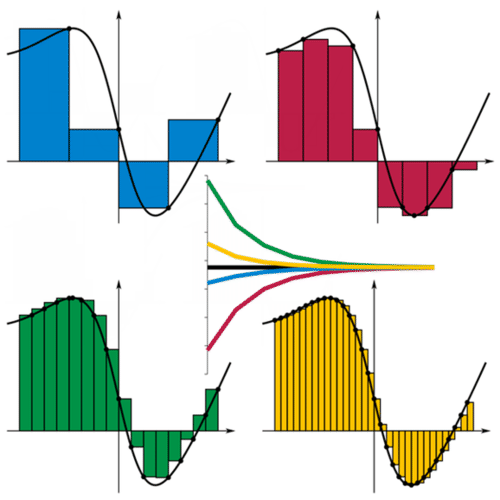
    F-D_0173D06A9BF3DF490EB82F6C3888352704DD6DC2E4DBA6A7653B7B6+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png

    Субінтервали створюються, коли інтервал розбивається на менші, однаково величини інтервали. Синє наближення використовує праві коробки для висоти кожного підінтервалу. Червоне наближення призначає висоті поля мінімальним значенням функції в кожному підінтервалі. Зелене наближення призначає висоті поля максимальним значенням функції в кожному підінтервалі. У жовтому наближенні використовуються ліві коробки. Прямокутники над віссю x матимуть позитивну площу, а прямокутники нижче осі x матимуть негативну площу у цьому контексті.

    Використання квадратів для оцінки площі під кривою називається Сумою Рімана. Візьміть функцію\(\ f(x)=\frac{1}{2} x-2\). Щоб обчислити суму Рімана (площа під кривою) між 1 та 9 функцією, спочатку намалюйте графік та поля.

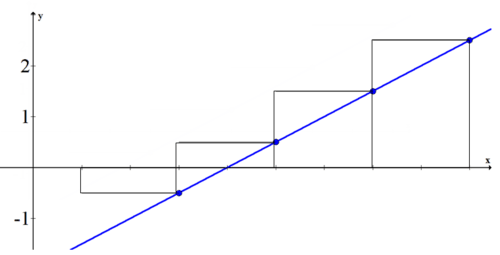
    F-D_погано BBB 683A64C3E1E32259372937AC9D14B17BA68fc007c5c437670+зображення_thumb_листівка_крихіткий+зображення_великий палець_листівка_крихітка_png

    Площа першого ящика в 2 рази перевищує висоту функції, оціненої в 3:

    \(\ 2 \cdot\left(\frac{1}{2} \cdot 3-2\right)=3-4=-1\)

    Оскільки ця коробка знаходиться під віссю x, його площа негативна.

    Площа для кожного з решти ящиків в 2 рази перевищує висоту функції, оціненої на 5, 7 і 9.

    \ (\\ почати {масив} {l}
    2\ cdot\ ліворуч (\ frac {1} {2}\ cdot 5-2\ праворуч) &=5-4 = 1\\
    2\ cdot\ ліворуч (\ frac {1} {2}\ cdot 7-2\ праворуч) &=7-4=3\
    2\ cdot\ ліворуч (\ frac {1} {2}\ cdot 9-2\ праворуч) &=9-4=5
    \ end {масив}\)

    Приблизна сума загальної площі під кривою становить: −1+1+3+5=8 квадратних одиниць.

    Усі чотири наближення площі, показані раніше, покращуються, оскільки кількість ящиків збільшується. Насправді межа кожного наближення, коли кількість підінтервалів (коробок) збільшується до нескінченності, є точною площею під кривою.

    Тут приходить ідея числення інтеграла. Інтеграл - це межа суми, оскільки кількість доданих збільшується до нескінченності. Сумманд - це одна з багатьох частин, які підсумовуються разом.

    \(\ \int f(x)=\lim _{n \rightarrow \infty} \sum_{i=1}^{n}(\text { Area of box } i)\)

    Символ зліва є символом числення інтеграла.

    Приклади

    Приклад 1

    Раніше вас попросили визначити, як далеко проїжджає машина за 8 секунд.

    Рішення

    Ви можете використовувати площу під кривою, щоб знайти загальну відстань, пройдену за перші 8 секунд. Оскільки квадратична крива, ви повинні вибрати кількість підінтервалів, які ви хочете використовувати, і чи потрібні праві або ліві поля для оцінки. Припустимо, ви вибрали 8 лівих коробок шириною один.

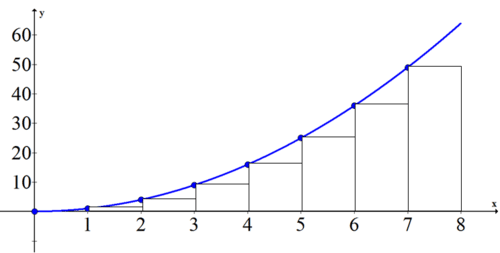
    F-D_52845ECE4E580261 FA377EF3665FA1C6797783B87DB64647C61AF266+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png

    х 0 1 2 3 4 5 6 7
    Площа коробки праворуч 1⋅0 1⋅1 1⋅4 1⋅9 1⋅16 1⋅25 1⋅36 1⋅49

    Приблизна сума - 1+4+9+16+25+36+49=140. Це означає, що автомобіль проїхав приблизно 140 метрів за перші 8 секунд.

    Приклад 2

    Оцініть точну площу під використовуваною раніше кривою\(\ f(x)=\frac{1}{2} x-2\), використовуючи формулу площі для трикутника.

    Рішення

    Пам'ятайте, що область під\(\ x\) віссю негативна, тоді як площа над\(\ x\) віссю позитивна.

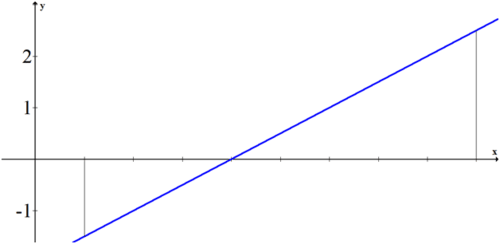
    F-D_93627 Дабі 7C095A611DAEB8EADE 36A8A1B48DB9E22561BE3A7+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png

    Негативна область:\(\ \frac{1}{2} \cdot 3 \cdot 1.5=\frac{9}{4}\)

    Позитивна область:\(\ \frac{1}{2} \cdot 5 \cdot 2.5=\frac{25}{4}\)

    Площа під кривою між 1 і 8:\(\ \frac{25}{4}-\frac{9}{4}=\frac{16}{4}=4\)

    Якщо порівняти цю відповідь з наближенням раніше, виявляється, що наближення шириною 2 одиниці виробляють площу зі значною похибкою.

    Приклад 3

    Логан подорожує на велосипеді зі швидкістю 20 миль/год протягом 3 годин. Потім вона сідає в машину і їздить 60 миль/год протягом 2 годин. Намалюйте як відстань проти часового графіка, так і швидкість проти часового графіка. Використовуйте область під аргументом кривої, щоб з'єднати два графіки.

    Рішення

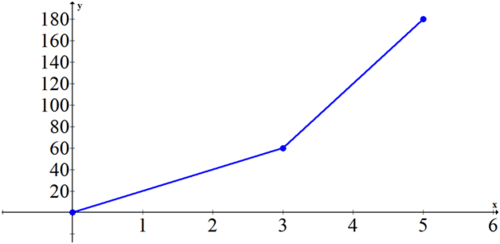
    Відстань проти часу:

    F-D_59A324DE986DAE A26677c62ec6D77CF52f7b2645FBA9269CAA097764+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png

    Ставка проти часу:

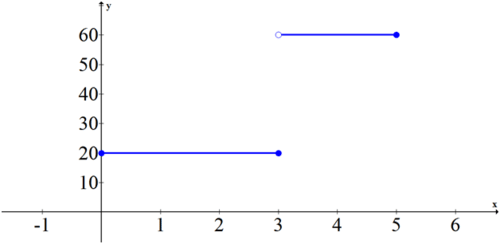
    F-D_088688C669D6FFAED 78B4E111F706E1D32BA2EFA89825A03FBC6B4FE+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png

    Нахил першого графа дорівнює 20 від 0 до 3, а потім 60 від 3 до 5. Другий графік - це графік нахилів з першого графа. Якщо обчислити площу другого графіка в ключових точках 0, 1, 2, 3, 4 і 5, ви побачите, що вони ідеально вирівнюються з точками на першому графіку.

    х Площа під кривою від 0 до x
    0 0
    1 20
    2 40
    3 60
    4 120
    5 180
    Приклад 4

    Орієнтуйте площу під кривою, використовуючи вісім підінтервалів і праві кінцеві точки.

    \(\ f(x)=3 x^{2}-1,-1 \leq x \leq 7\)

    Рішення

    Хоча графік корисний для візуалізації проблеми, і малювання кожного поля може допомогти надати значення кожному резюме, це не завжди потрібно. Оскільки на загальному інтервалі −1≤x≤7 буде 8 підінтервалів, кожен інтервал матиме ширину 1. Висота кожного інтервалу буде знаходитися в правій кінцевій точці кожного підінтервалу (0, 1, 2, 3, 4, 5, 6, 7).

    \(\ \sum \text { height } \cdot \text { width }=\sum_{i=0}^{7}\left(3 i^{2}-1\right) \cdot 1=412\)

    Приклад 5

    Орієнтуйте площу під кривою, використовуючи двадцять субінтервалів і ліві кінцеві точки.

    \(\ f(x)=x^{x}, 1 \leq x \leq 3\)

    Рішення

    Коли кількість субінтервалів стане великим, а підінтервали стануть надзвичайно вузькими, намалювати точну картинку буде неможливо. Ось чому використання позначень підсумовування та продумування того, якими будуть індекси та аргумент, неймовірно важливо. З 20 субінтервалами між [1,3] кожен інтервал буде шириною 0,1. Ліва кінцева точка означає, що перше поле має висоту,\(\ f(1)\) а друге поле має висоту\(\ f(1.1)\).

    \ (\\ почати {вирівняний}
    \ сума\ текст {висота}\ cdot\ текст {ширина} &= f (1)\ cdot 0.1+f (1.1)\ cdot 0,1+f (1,2)\ cdot 0.1+\ cdots+f (2.9)\ cdot 0,1\\
    &= 0,1 (f (1) +f (1.1) +\ cdots f (2.9)\
    &=0.1\ cdot\ sum_ {i=10} ^ {29} f\ ліворуч (\ frac {i} {10}\ праворуч)\\
    & =0.1\ cdot\ sum_ {i = 10} ^ {29}\ ліворуч (\ frac {i} {10}\ праворуч) ^ {\ ліворуч (\ frac {i} {10}\ праворуч)}\\\
    &\ приблизно 12.47144
    \ кінець {вирівняний}\)

    Ваш калькулятор може обчислити підсумовування, коли ви йдете в меню математики.

    F-D_C8E2E8F7B7FB91A1FF281713A14B0AAB707e51a23111c693ed8c7+зображення_thumb_поштова листівка_крихіткий+зображення_великий палець_поштова листівка_крихітка_png

    Рецензія

    1. Орієнтуйте площу під кривою, використовуючи вісім підінтервалів і праві кінцеві точки.

      \(\ f(x)=x^{2}-x+1,0 \leq x \leq 8\)

    2. Орієнтуйте площу під кривою, використовуючи вісім підінтервалів і ліві кінцеві точки.

      \(\ f(x)=x^{2}-2 x+1,-4 \leq x \leq 4\)

    3. Орієнтуйте площу під кривою, використовуючи двадцять субінтервалів і ліві кінцеві точки.

      \(\ f(x)=\sqrt{x+3}, 0 \leq x \leq 4\)

    4. Орієнтуйте площу під кривою, використовуючи 100 субінтервалів і лівих кінцевих точок. Порівняйте з вашою відповіддю з #3.

      \(\ f(x)=\sqrt{x+3}, 0 \leq x \leq 4\)

    5. Орієнтуйте площу під кривою, використовуючи вісім підінтервалів і ліві кінцеві точки.

      \(\ f(x)=\cos (x), 0 \leq x \leq 4\)

    6. Орієнтуйте площу під кривою, використовуючи двадцять субінтервалів і ліві кінцеві точки.

      \(\ f(x)=\cos (x), 0 \leq x \leq 4\)

    7. Орієнтуйте площу під кривою, використовуючи 100 субінтервалів і лівих кінцевих точок.

      \(\ f(x)=\cos (x), 0 \leq x \leq 4\)

    Наступний графік показує швидкість (у милі на годину) проти часу (у годині) для автомобіля.

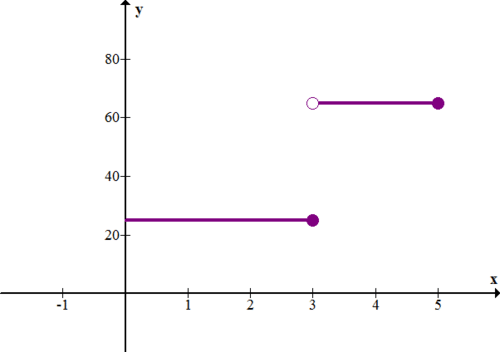
    F-D_FF3D FAA04F88E98EF1C7CAF6F172E5BE18FF6EF67F48D0F369D2D1B5+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png

    8. Опишіть, що відбувається з автомобілем.

    9. Як далеко проїхала машина за 5 годин?

    Наступний графік показує швидкість (у футах в секунду) проти часу (у секундах) для автомобіля.

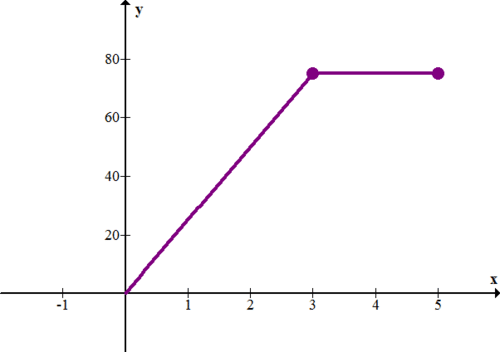
    F-D_011 дБ86ФДБФ FE51CE53ДК81Д2БД67Б97Ф9ДДБ1DAE9630FB4204+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихіткий.PNG

    10. Опишіть, що відбувається з автомобілем. Зокрема, що відбувається в перші 3 секунди?

    11. Як далеко проїхала машина за 5 секунд?

    Наступний графік показує функцію\(\ f(x)=-(x-4)^{2}+16\), яка представляє швидкість (у футах в секунду) проти часу (у секундах) для бігуна.

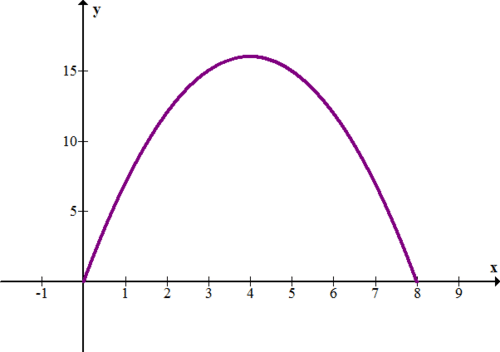
    F-D_ACE 5732E077A1040E6A6a679D3BEF736E162BE5901DB86CB5D6FDE8FA9+зображення_thumb_поштова листівка_крихітка_зображення_великий палецька_листівка_крихіткий.PNG

    12. Опишіть, що відбувається з Раннер. Зокрема, що відбувається через 4 секунди?

    13. Використовуйте прямокутники, щоб наблизити загальну відстань (у футах), яку бігун пройшов за 8 секунд. Постарайтеся отримати якомога краще наближення.

    14. Поясніть, як інтеграл схожий на протилежність похідної.

    15. Як інтеграли співвідносяться з сумами?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 14.9.

    Лексика

    Термін Визначення
    Δ Символ «Δ», читається «дельта», використовується для позначення «зміни в», як в «зміна швидкості з плином часу»\(\ =\frac{\Delta v}{t}\).
    певний інтеграл Певний інтеграл дає площу між віссю x і кривою через певний інтервал.
    межа Межа - це значення, до якого наближається вихід функції, коли вхід функції наближається до заданого значення.
    субаінтервали Субінтервали створюються, коли інтервал розбивається на менші однаково величини інтервали.
    виклик Сума - це вираз, що підсумовується. Вона безпосередньо слідує за символом сигми.

    Атрибуції зображень

    1. [Рисунок 1]
      Кредит: Фонд CK-12;
      Джерело KsmRQ: https://commons.wikimedia.org/wiki/File:Riemann_sum_convergence.png
       Ліцензія: CC BY-SA