1.4: Кількісні навички

Last updated
Save as PDF

Page ID: 6556

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Змінні

Експериментальна наука розглядає причинно-наслідкові типи зв'язків. Контрольовані експерименти варіюють один з факторів або рис, щоб спостерігати вплив на інший фактор або рису. Ці фактори називаються змінними. Залежна змінна - це те, що спостерігається і, як очікується, зміниться в результаті модифікації іншого фактора в експерименті. Тобто результат залежить від іншого фактора. Інша назва залежної змінної - відповідна змінна. Незалежна змінна - це фактор або умова, яка змінюється або змінюється експериментатором. Іноді очікування - це умова, яка змінюється, роблячи незалежну змінну: час. Оскільки ми змінюємо незалежну змінну, її ще називають маніпульованою змінною.

Графік лінії

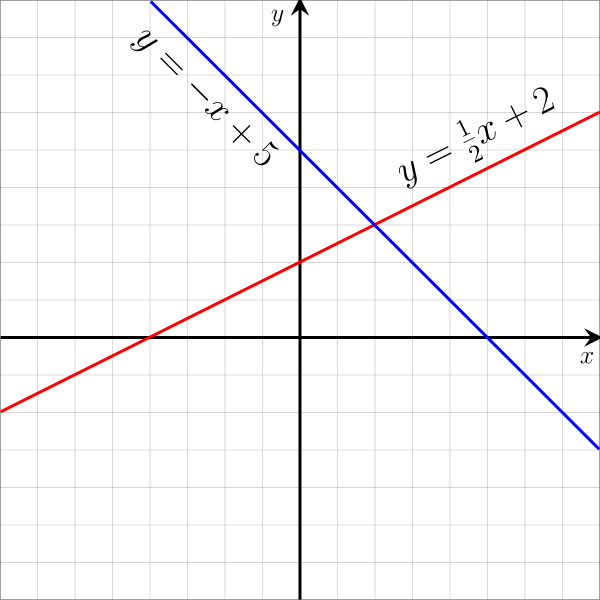
Графік, що відображає 2 рядки та їх рівняння

Рядок можна описати математично рівнянням:

Це називається формою нахилу-перехоплення. 2 змінні y та x відносяться до координат уздовж кожної осі. Термін m позначає зміну значень y над зміною значень x. Це називається нахилом лінії. Термін b, перехоплення y, - це значення y, де лінія перетинає вісь y.

$m =\ розрив {y_2-y_1} {x_2-x_1}$ АБО $m =\ гідророзриву {\ Дельта y} {\ Дельта х}$

Так визначається ухил лінії (м).

Нахил прямої вказує на зв'язок між двома змінними, x і y. рівняння прямої вказує нам, що «y» виникає як функція змін до «x». Іноді це представлено рівнянням. Оскільки «y» залежить від «x», «y» - залежна змінна, а «x» - незалежна змінна. Як змінюється «х», як змінюється «y» у відповідь? Це те, що нам відкриває схил.

Для отримання додаткової інформації перейдіть за наступним посиланням.

Діяльність схилу

Графічні лінії

Натисніть тут, щоб запустити моделювання.

Діяльність побудови даних

Використовуйте наступні дані USDA для побудови графіка розсіювання та створення лінії тренду.
Використовуйте інформацію з таблиці нижче або завантажити (текстовий файл, який можна відкрити в блокноті/textedit)
Дотримуйтесь підручника про те, як графікувати розсіювач з лінією найкращого підгонки (лінія тренду)
Або скористайтеся цим підручником у plot.ly
- Показувати рівняння лінії тренду на графіку
- Переконайтеся, що «фунти моцарели» є віссю y
- Переконайтеся, що «Рік» є віссю x
- Пам'ятайте, що не використовуйте лінійний графік

Рік	фунтів моцарели
2000	9.33
2001	9.70
2002	9.66
2003	9.65
2004	9.94
2005	10.19
2006	10.52
2007	11.02
2008	10.57
2009	10.63

Що ми дізнаємося?

Що говорить нам цей розсіювач про взаємозв'язок між споживанням моцарели по відношенню до років?
Як би цей графік вплинув на те, як ви інвестуєте в компанію з виробництва сиру моцарелла? Чи можете ви передбачити що-небудь про майбутнє споживання сиру?
На що вам вказує нахил цієї лінії?
1. Використовуйте математику, щоб проілюструвати цей момент.
2. Схил має одиницю, пов'язану з «фунтами» і «рік», що це за одиниця?

Створення лінії найкращої посадки

Не всі зібрані точки будуть падати на пряму лінію. Лінія найкращого підгонки або лінія тренду наближає середнє значення цих точок за допомогою математичного процесу, який називається методом найменших квадратів. Хоча можна «очне яблуко» цієї лінії, метод найменших квадратів використовує дані, щоб мінімізувати відстань від усіх цих точок до лінії, щоб мати ефект усереднення.

Створіть стовпець даних для значень «x», «y» значень, x ² та xy
Внизу цих стовпців підсумуйте дані. σ х, σ, σ х ², σxy
Обчисліть ухил з цих значень
- $m =\ frac {N (\ Сигма xy) -\ Сигма х\ Сигма у} {N (\ Сигма х ^2) - (\ Сигма х) ^2}$ (де N = кількість записів у стовпці)
Обчисліть y-перехоплення з цих значень
- $b =\ frac {N (\ Сигма у) - m (\ Сигма х)} {N}$
Що забезпечує використання функції

Регресія найменших квадратів

Натисніть тут, щоб запустити моделювання.