2.8: Підсумкові питання

Last updated
Save as PDF

Page ID: 3618

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

1. Визначте загальну висоту дерев, проілюстрованих нижче. Зверніть увагу на горизонтальні відстані та масштаб нахилу, що використовуються для кожного.

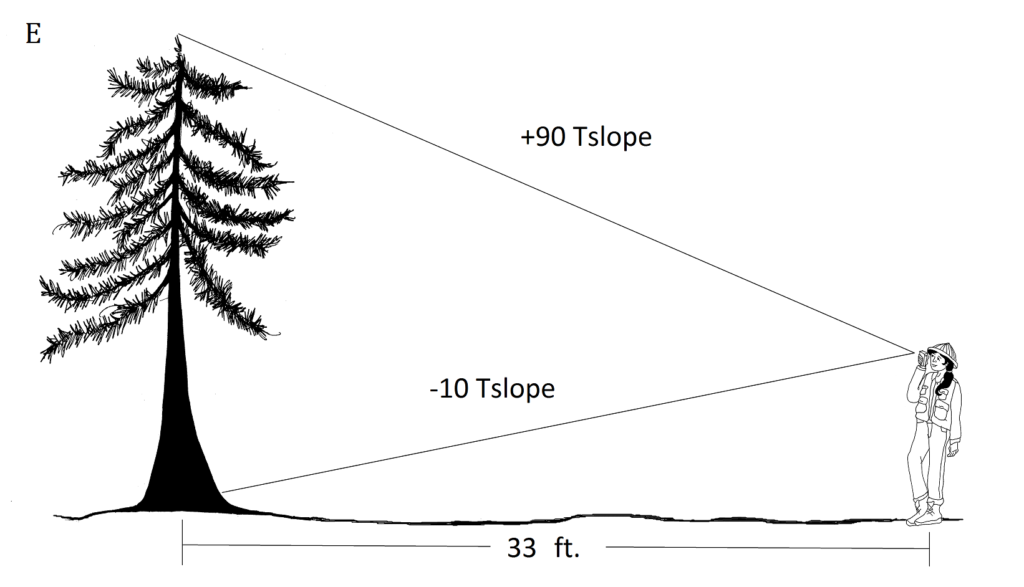
2. Як повинна бути визначена загальна висота дерева з плоскою вершиною нижче?

3. Розрахуйте висоту більш стрункого дерева нижче.

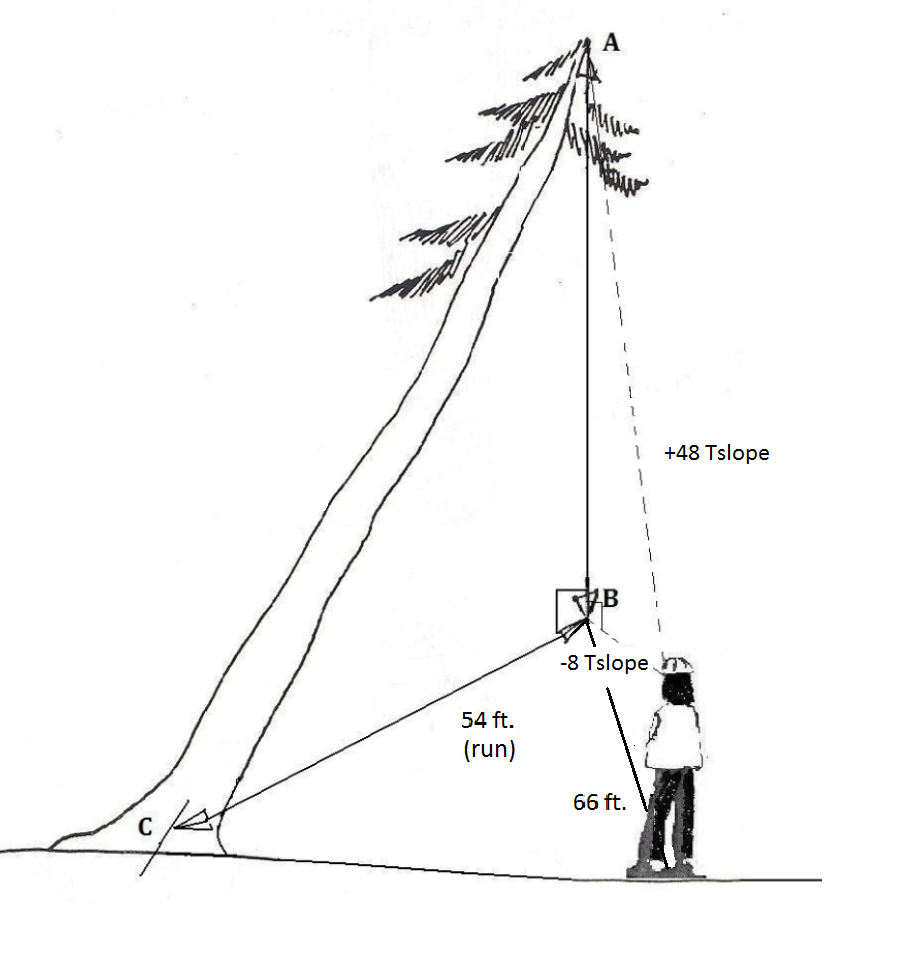
Відповіді на підсумкові запитання

1. A.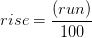 (% нахилу)

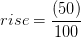(137+11)

підйом (висота) = 74 футів

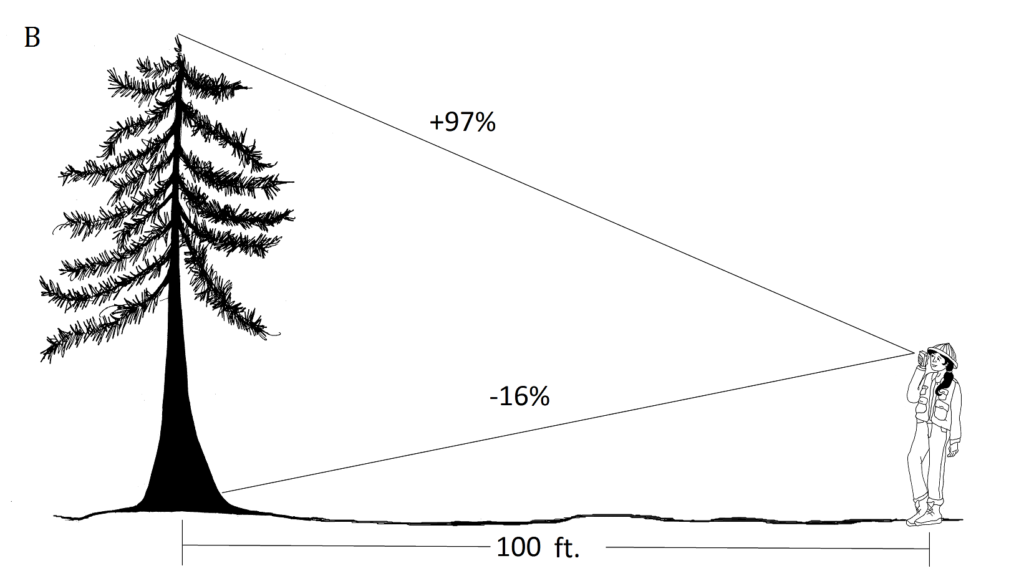
І.Б.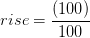 (97+16)

= 113 футів

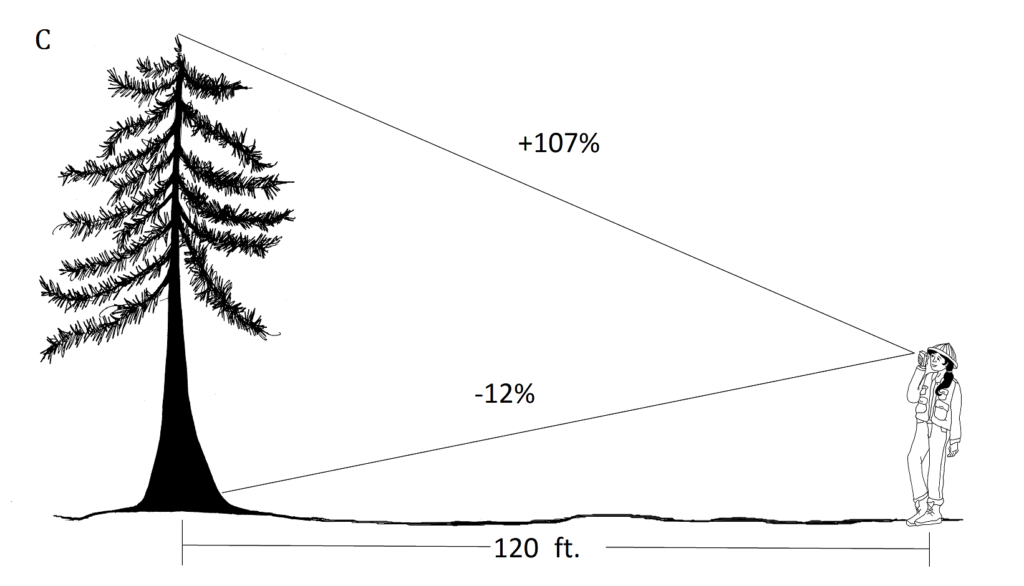
І.К.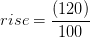 (107+12)

= 143 футів

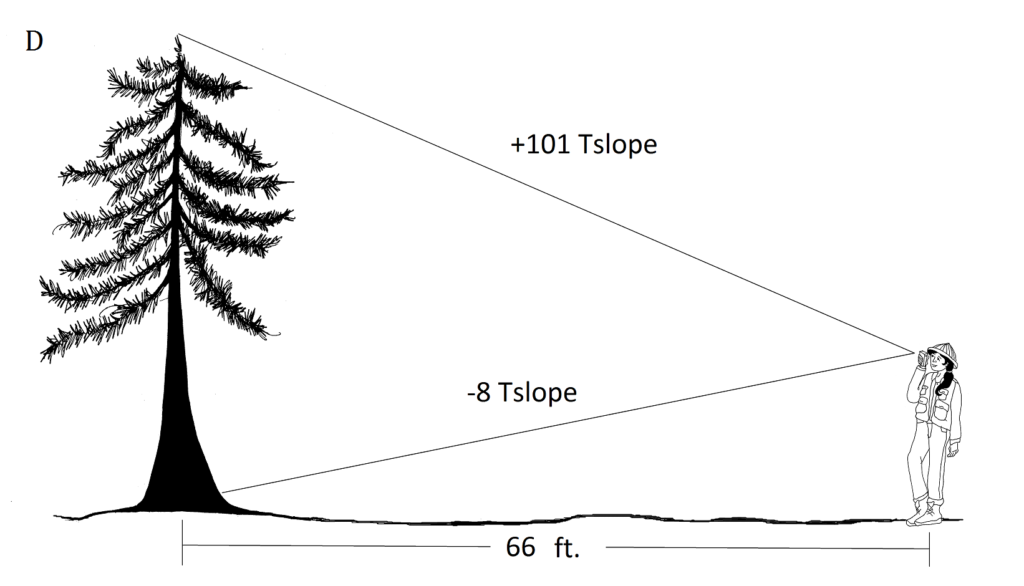
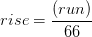Ідентифікатор (Тскопе)

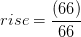(101+8)

підйом (висота) = 109 футів

ТОБТО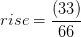 (90+10)

= 50 футів

2. Верхівку дерева доведеться реконструювати через зламаної верхівки. Це можна зробити за допомогою сусіднього дерева, схожого за розміром і конусності в якості еталону.

3. а. підйом лінії падіння від верхівки дерева на землю =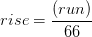 (Цлопе)

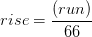(48+8)

= 56 футів

b Горизонтальна відстань від основи дерева до лінії падіння становить 54 фути. Таким чином у нас є дві сторони прямокутного трикутника.

Використовуючи теорему Піфагора для визначення довжини дерева (гіпотенузи):

a ² + b ² = c ² де:

56 ² + 54 ² = с ²

6052 = с ²

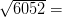78 футів