7.4: Лінійне програмування

Last updated
Save as PDF

Page ID: 31582

Franz S. Hover & Michael S. Triantafyllou
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

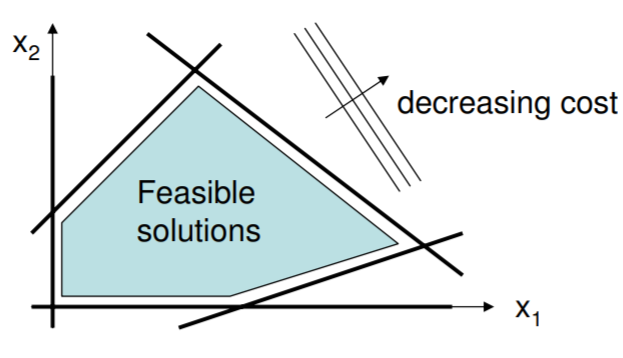
Розглянемо тепер випадок, що вартість - це лінійна функція\(n\) параметрів. Очевидно, що рішення не існує, якщо простір параметрів не обмежений, і дійсно рішення гарантовано знаходиться на кордоні. Ситуація добре проілюстрована в двох вимірах\((n = 2)\), приклад яких наведено нижче. Тут показано п'ять лінійних кордонів нерівності; не\(x\) допускаються поза можливою областю. У загальному випадку можуть бути присутніми як обмеження рівності, так і нерівності.

Графік, що показує двовимірну область, обмежену 5 лінійними нерівностями, в межах яких має лежати розв'язок. — Малюнок\(\PageIndex{1}\): графік двовимірної області, обмеженої 5 лінійними нерівностями, де вартість - лінійна функція двох параметрів, зазначених на осях. Хоча вартість може бути більш оптимальною за межами обмеженого регіону, всі можливі рішення повинні лежати в цьому регіоні.

Характер проблеми - все лінійне, і включає нерівність і, можливо, обмеження рівності - допускає спеціальні і потужні алгоритми, які ефективні навіть у дуже великих вимірах, наприклад, в тисячах. У нижчих вимірах ми можемо звернутися до інтуїції, отриманої з фігури, щоб побудувати простіший метод для малих систем, скажімо, до десяти невідомих.

Перш за все, з малюнка видно, що рішення повинно лежати на одній з кордонів. Рішення фактично лежить у вершині\(n\) гіперповерхонь розмірності\(n-1\). Така гіперповерхня являє собою лінію в двовимірному просторі, площину в тривимірному просторі і так далі. Ми скажемо, що лінія в трипросторі - це перетин двох площин, а значить, еквівалентна двом гіперповерхням розмірності два. Можна перевірити, що гіперповерхня розмірності\(n-1\) визначається одним рівнянням.

Якщо обмежень рівності немає, то ці\(n\) гіперповерхні, що утворюють вершину розв'язку, є підмножиною обмежень\(I\) нерівності. У нас взагалі буде\(I>n\). Якщо існують також обмеження\(E<n\) рівності, то рішення лежить на перетині цих гіперповерхонь\(E\) рівності та\(n-E\) інших гіперповерхонь, взятих з обмежень\(I\) нерівності. Звичайно, якщо\(E=n\), то у нас є тільки лінійна система для вирішення. Таким чином, ми маємо комбінаторичну задачу; розглянемо лише випадок нерівностей, а потім змішаний випадок.

\(I\)нерівності, відсутні рівності. \(n\)нерівностей визначить вершину розв'язку. Кількість комбінацій рівнянь\(n\) обмежень серед\(I\) варіантів є\(I!/(I −n)!n!\). Алгоритм: Для кожної комбінації (індексованої\(k\), скажімо) по черзі вирішуйте лінійну систему рівнянь, щоб знайти рішення\(x_k\). Переконайтеся, що рішення не порушує жодного з інших обмежень\(I-n\) нерівності. З усіх рішень, які є здійсненними (тобто вони не порушують ніяких обмежень), підберіть оптимальний - він оптимальний.
\(I\)нерівності,\(E\) рівності. Рішення включає всі рівності та обмеження\(n-E\) нерівності. Кількість комбінацій рівнянь\(n-E\) обмежень серед\(I\) варіантів є\(I! / (I-n+E)! (n-E)!\). Алгоритм: Для кожної комбінації (індексованої з\(k\)) по черзі вирішуйте лінійний набір рівнянь, щоб дати кандидатське рішення\(x_k\). Переконайтеся, що рішення не порушує жодного з інших обмежень\(I-n+E\) нерівності. З усіх посильних рішень підберіть оптимальний - він оптимальний.

Наведений вище приблизний рецепт передбачає, що жодна з гіперповерхонь не паралельна; паралельні обмеження не перетинаються і не існує розв'язку лінійного набору рівнянь. На щастя, такі випадки можуть бути легко виявлені (наприклад, шляхом перевірки на сингулярність матриці) і класифікуються як нездійсненні. На наведеному вище малюнку,\(I = 5\) і\(n = 2\). Звідси є\(5!/(5-2)!2! = 10\) комбінації, щоб спробувати: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE. Лише п'ять очевидні, оскільки деякі перехрестя знаходяться за межами зазначеної області (Чи можете ви знайти їх усі?).

Підхід лінійного програмування є надзвичайно цінним у багатьох сферах політики та фінансів, де витрати масштабуються лінійно з кількістю, а нерівності є звичайним явищем. Існує також безліч інженерних додатків, через поширеність лінійного аналізу.