10.6: Кінцева міцність пластин

У попередньому розділі ми показали, що після вигину пластина продовжує приймати додаткове навантаження, але з половиною своєї жорсткості перед вигином. Для того щоб зрозуміти, що буде далі, розглянемо розподіл напружень стиснення в площині\(\sigma_{xx}\) при\(x = a\). З рівнянь (10.2.10-10.2.11) і (?? ) складовими\(\sigma_{xx}\) є

\[\sigma_{xx}(y) = \frac{N_{xx}}{h} = \frac{E}{1 − \nu^2} \left[ −(1 − \nu^2) \frac{u_o}{a} + \frac{\pi^2}{2} \left(\frac{w_o}{a} \right)^2 \sin^2 \frac{\pi y}{a} \right] \]

Перший член являє собою негативне, стискаюче напруження, рівномірне по ширині пластини. Другий термін описує зняття розтягуючих напружень, що утворюються кінцевим обертанням. Співвідношення між\(w_o\) і\(u_o\) задається рівнянням (?? ) і зображено на малюнку (10.5.2). Графік функції\(\sigma_{xx}(y)\) для декількох значень часового параметра\(u_o\) показаний на малюнку (\(\PageIndex{1}\)). Зверніть увагу, що криві, позначені A, B, C і D, відповідають відповідним точкам на рис. (10.5.2) і (10.5.3).

Рисунок\(\PageIndex{1}\): Перерозподіл напружень стиснення по навантаженому краю і просте наближення фон Карманом.

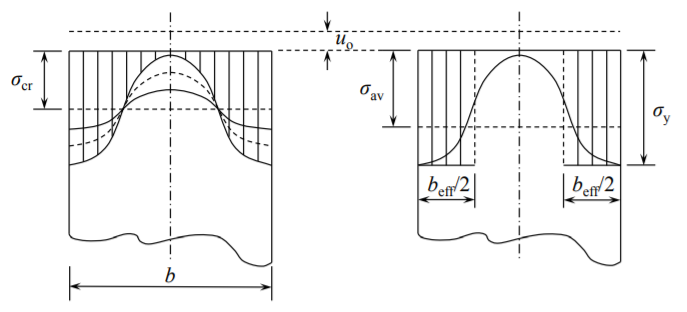
При збільшенні стиснення пластини відбувається перерозподіл напружень по навантаженої кромці\(x = 0\) і\(x = a\). Напруга на розвантаженому краю\(y = 0\) і\(y = a\) продовжує зростати, тоді як напруга на площині симетрії пластини\(y = \frac{a}{2}\) зменшується до нуля.

Саме німецький вчений і інженер Теодор фон Карман в 1932 році скористався спостереженням, представленим на малюнку (\(\PageIndex{1}\)). Він припускав, що центральна, ненавантажена частина плити несе нульове напруження, в той час як крайова зона, кожна з ширини\(b_{\text{eff}}/2\) досягає межі текучості в точці граничного навантаження. В якості відправної точки фон Карман використав вираз для критичного навантаження на вигин\(N_c\) і розглянув співвідношення між напругою на навантаженому краю\(\sigma_e\) і шириною пластини.\(b\)

\[\sigma_e = \frac{N_e}{h} = \frac{N_c}{h} = \frac{4\pi^2D}{hb^2} = \frac{4\pi^2Eh^2}{12(1 − \nu^2)b^2} = 1.9^2E\left(\frac{h}{b}\right)^2\]

Зазвичай\(b\) це вхідний параметр, а напруга\(\sigma_e\) - невідома величина. Винахідливість фон Кармана полягала в тому, що він перевернув те, що відомо і невідомо в Рівнянні (?? ). Він запитав, якою має бути ширина пластини,\(b_{\text{eff}}\) щоб напруга краю досягала межі текучості. Таким чином

\[\sigma_y = 1.9^2E\left(\frac{h}{b_{\text{eff}}}\right)^2\]

Розв'язування наведеного вище рівняння для\(b_{\text{eff}}\)

\[b_{\text{eff}} = 1.9h \sqrt{\frac{E}{\sigma_y}}\]

Беручи для прикладу\(E = 200000\)\(b_{\text{eff}}\sigma_y = 320\) МПа, МПа, ефективна ширина стає

\[b_{\text{eff}} = 1.9h \sqrt{625} = 47.5h \]

Ефективна ширина залежить від модуля Юнга, а напруга плинності пропорційна товщині пластини. Приблизно 40-50 товщин плити біля країв несе навантаження, що залишилася центральна частина не ефективна. Сумарне навантаження на плиту може виражатися двома способами

\[P_{\text{ult}} = b_{\text{eff}} \cdot \sigma_y = b \cdot \sigma_{\text{av}}\]

де\(\sigma_{\text{av}} = \sigma_{\text{ult}}\) - середнє навантаження на навантажену кромку в точці граничної міцності,

\[\frac{\sigma_{\text{av}}}{\sigma_{\text{ult}}} = \frac{b_{\text{eff}}}{b} = 1.9 \frac{h}{b} \sqrt{\frac{E}{\sigma_y}}\]

Група параметрів

\[\beta = \frac{b}{h} \sqrt{\frac{\sigma_y}{E}}\]

називається коефіцієнтом стрункості пластини. Зверніть увагу, що це інше поняття, ніж коефіцієнт стрункості колонки\(l/\rho\). Використовуючи параметр\(\beta\), гранична міцність пластини, нормована за межі текучості, становить

\[\frac{\sigma_{\text{ult}}}{\sigma_{y}} = \frac{1.9}{\beta}\]

Нагадаємо, що нормоване напруження вигину пружної пластини становить

\[\frac{\sigma_{\text{cr}}}{\sigma_{y}} = \left(\frac{1.9}{\beta}\right)^2\]

Графіки обох функцій показані на малюнку (\(\PageIndex{2}\)).

З цієї цифри можна виділити коефіцієнт критичної стрункості.

\[\beta_{\text{cr}} = 1.9 \]

коли як граничне навантаження, так і критичне навантаження на вигин досягають виходу. З рівняння (?? ) видно, що при\(\beta = \beta_{\text{cr}}\), ефективна ширина дорівнює ширині пластини,\(b_{\text{eff}} = b\).

Малюнок\(\PageIndex{2}\): Залежність напруги вигин і граничного напруження від коефіцієнта стрункості.

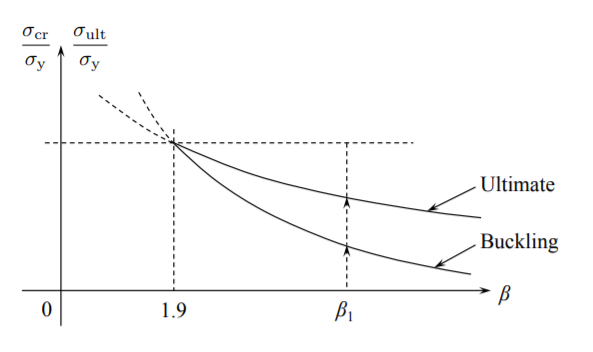
Усунення параметра\(\beta\) між рівняннями (?? ) і (?? ), кінцева напруга розглядається як геометричне середнє між напругою текучості та критичним напруженням вигин

\[\sigma_{\text{ult}} = \sqrt{\sigma_{\text{cr}} \cdot \sigma_{y}}\]

Наприклад, безперервне навантаження пластини з\(\beta_1\) коефіцієнтом стрункості спочатку зіткнеться з кривою вигин, а потім кривою граничної міцності, як показано на малюнку (\(\PageIndex{2}\)). Вищеописаний аналіз був справедливим для пластин, які просто підтримуються вздовж усіх чотирьох країв, для яких коефіцієнт вигину є\(k_c = 4\). Для іншого типу підтримки Рівняння (?? ) як і раніше діє з коефіцієнтом 1.9 заміненим на 1.9\(\frac{k_c}{4}\).

Багато зусиль було присвячено в минулому, щоб експериментально підтвердити передбачення теорії ефективної ширини фон Кармана. Було встановлено, що невелика поправка до рівняння (?? ) забезпечує хорошу підгонку більшості тестових даних

\[\frac{\sigma_{\text{ult}}}{\sigma_{y}} = \frac{b_{\text{eff}}}{b} = \frac{1.9}{\beta} − \frac{0.9}{\beta^2}\]

Наприклад, для відносно короткої (кремезної пластини) вихідна формула над прогнозує на 15%\(\beta = 2\beta_{\text{cr}} = 3.8\), ніж більш точне емпіричне рівняння (?? ). Для струнких пластин різниця невелика. Останнє стало основою для проектування тонкостінних стискаючих елементів у більшості вітчизняних та міжнародних стандартів, таких як AISI, Aluminium Association та AISC.