Skip to main content
LibreTexts - Ukrayinska

10.4: Вигин секцій

  1. Last updated
  2. Save as PDF
  • Page ID
    33261

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Холодні або зварні профілі зустрічаються практично в кожному аспекті інженерної практики. Типові геометрії поперечного перерізу призматичних елементів наведені на малюнку (\(\PageIndex{6}\)).

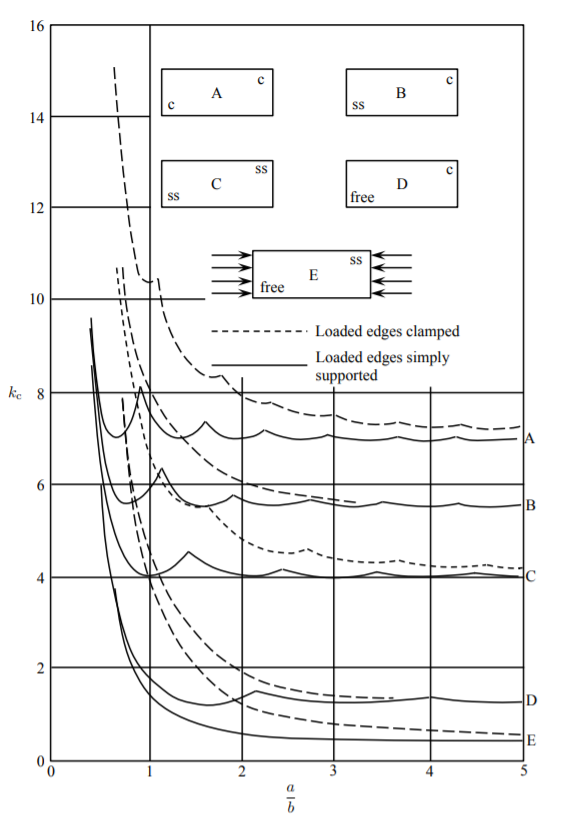
    10.4.1.png
    Рисунок\(\PageIndex{1}\): Вплив граничних умов на коефіцієнт вигину прямокутних пластин, що піддаються внутрішньоплощинним граничним умовам.
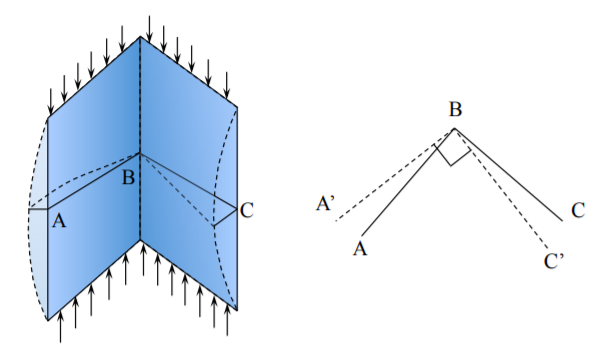
    10.4.2.png
    Малюнок\(\PageIndex{2}\): Режим вигину кутового елемента.
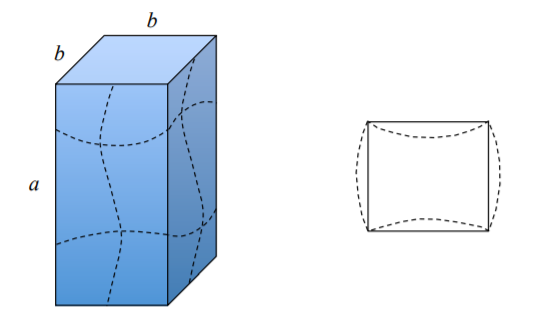
    10.4.3.png
    Малюнок\(\PageIndex{3}\): Режим вигину призматичного квадратного стовпа.
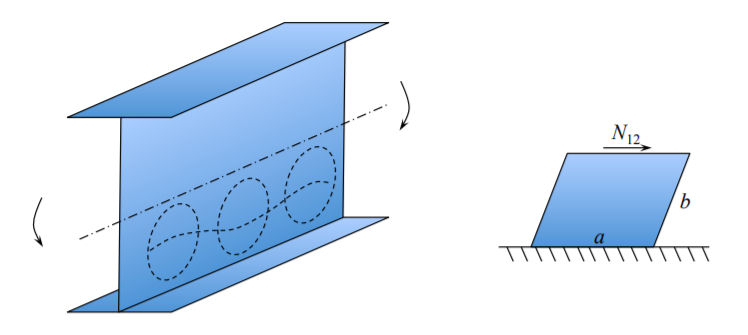
    10.4.4.пнг
    Малюнок\(\PageIndex{4}\): Вигин через зсув або згинання.
    10.4.5.пнг
    Малюнок\(\PageIndex{5}\): Фотографія зсуву вигин пластини, що представляє малюнок пошкодження на корпусі судна, нанесеного при заземленні.
    10.4.6.png
    Малюнок\(\PageIndex{6}\): Деякі типові відкриті і замкнуті форми поперечного перерізу призматичних елементів.

    Крім симетричного кута, «Т», хрестоподібного і квадратного профілю короба, де міцність на вигин всієї секції є сумою навантажень на вигин пластини, що сприяють, аналіз іншої форми вимагає врахування стримуючих згинальних моментів і умов безперервності уздовж загальних країв. Найпростіший спосіб проілюструвати проблему - розглянути прямокутний перетин призматичної колони, рис. (\(\PageIndex{7}\)). Відповідно до рівняння (?? ) навантаження на вигин обернено пропорційна ширині плити. Дві протилежні ширші пластини хотіли б спочатку застебнути, але більш короткі сторони не готові застібатися\(k = 4\). Вони забезпечують затиснуту граничну умову для більш широких фланців, для яких\(k \cong 7\). Повинна бути передача інформації між сусідніми табличками, щоб вони були «в симпатії» один до одного з різними\(k_c\).

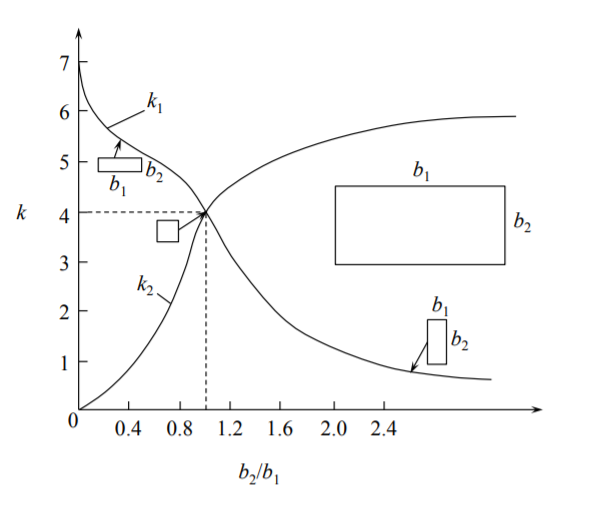
    10.4.7.пнг
    Малюнок\(\PageIndex{7}\): Коефіцієнти вигину прямокутної пластини як функція\(b_2/b_1\).

    Чисельно отримана функція\(k_1(b_2/b_1)\) показана на малюнку (\(\PageIndex{7}\)) суцільною лінією. Коефіцієнт вигину однозначно пов'язаний з\(k_1\) аналізом попереднього вигину. Перед вигином деформації і стискаючі напруги в сусідніх пластин однакові.

    \[\sigma_1 = \frac{N_1}{h_1} = \sigma_2 \frac{N_2}{h_2}\]

    де

    \[N_1 = k_1 \frac{\pi^2 D_1}{b^2_1}, \quad N_2 = k_2 \frac{\pi^2 D_2}{b^2_2}\]

    З вищенаведеного рівняння випливає, що

    \[k_2 = k_1 \left( \frac{b_2}{b_1} \right)^2\]

    \(k_1\)показано на малюнку (\(\PageIndex{7}\)) (суцільна лінія). Коефіцієнт вигину,\(k_2\) розрахований з Рівняння (?? ) показана на цьому ж малюнку пунктирною лінією. За допомогою наведеного вище результату можна довести, що при заданій вазі (площі поперечного перерізу) квадратна колона матиме найбільший опір вигинаючи для всіх прямокутних форм.

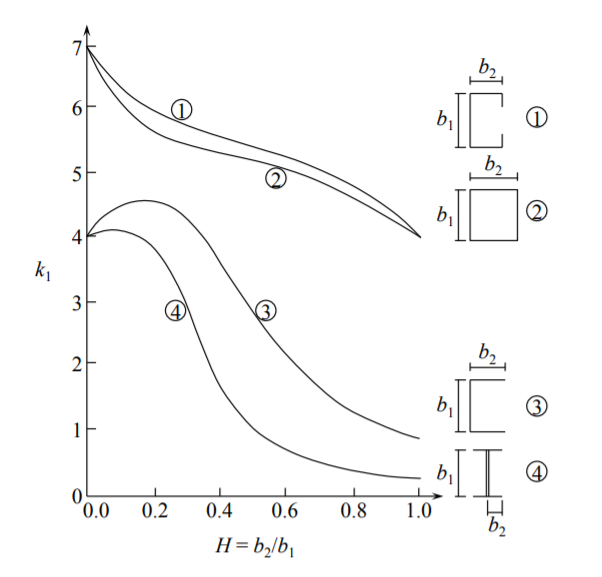
    Для більш складної форми поперечного перерізу коефіцієнт вигину може бути представлений в графічному вигляді, як показано на малюнку (\(\PageIndex{8}\)). Знаючи коефіцієнт\(k_1\) вигину для фланця шириною\(b_1\) і товщиною\(h_1\), коефіцієнти вигину всіх інших фланців потім обчислюються з:

    \[k_i = k_1 \left(\frac{h_ib_1}{h_1b_i}\right)\]

    У більшості випадків нічого драматичного не відбувається в точці вигин. Чисто стискаючий стан переходить в комбіноване згинання/стиснення, але пластина продовжує нести додаткове навантаження зі зниженою жорсткістю. Відповідь після вигину та граничне навантаження розглядається в наступному розділі цього розділу.

    10.4.8.пнг
    Малюнок\(\PageIndex{8}\): Коефіцієнти вигину для чотирьох типів перетинів.