7.6: Теорема Кастільяно

Ця теорема застосовується до статично визначеним структурам і системі, що піддаються зосередженим силам або моментам. Розподіл згинальних моментів можна однозначно визначити з глобальної рівноваги як функції сил,$U = U(P)$. Загальна потенційна енергія

$$\prod = U(P) − P w_o$$

Для заданої амплітуди$w_o$ відхилення величину навантаження регулюють себе таким чином, щоб загальна потенційна енергія була нерухомою. Математично

$$\delta [\prod (P)] = \delta [U(P) − P w_o] = \frac{dU}{dP} \delta P − w_o \delta P = \left[ \frac{dU(P)}{dP} − w_o \right] \delta P = 0$$

Доведено, що зміщення під силою в напрямку сили дорівнює похідній пружної енергії, що зберігається по відношенню до сили.

Для того щоб інтерпретувати стаціонарне властивість$\prod$, розглянемо консольну балку з силою$P$ на її кінчику. Розподіл згинального моменту є$M(x) = P(l − x)$. Давайте виберемо формулювання сили загальної потенційної енергії, Рівняння (?? ). Загальна потенційна енергія

$$[\prod = \frac{P^2}{2EI} \int_{0}^{l} (l − x)^2 dx − P w_o \label{8.49}$$

Після інтеграції

$$\prod(P) = P \left( \frac{Pl^3}{6EI} − w_o \right)$$

Графік цієї функції показаний на рис. ($\PageIndex{1}$).

Малюнок$\PageIndex{1}$: Параболічна варіація загальної потенційної енергії з силою$P$ для заданого центрального відхилення.

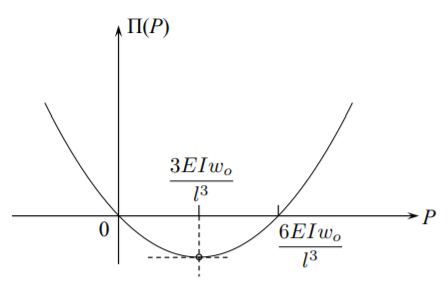
Парабола має два$P_1 = 0$ корені в і в$P_2 = \frac{6EIw_o}{l^3}$. Стаціонарна точка знаходиться в

$$P = \frac{3EIw_o}{l^3} \label{8.51}$$

що є точним рішенням проблеми.

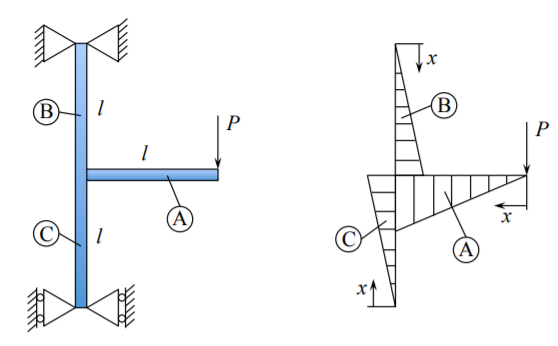
В якості ілюстрації розглянемо дві прості структурні системи. Перша система з двох балок показана на малюнку ($\PageIndex{2}$).

Ця проблема вирішувалася раніше за допомогою переміщень і безперервності нахилу. Випливає набагато просте рішення. Розподіли згинального моменту

$$\text{ Beam (A) } \; M(x) = −P x \; 0 < x < l \\ \text{ Beam (B) } \; M(x) = \frac{1}{2} P x \; 0 < x < l \\ \text{ Beam (C) } \; M(x) = − \frac{1}{2} P x \; 0 < x < l$$

Рисунок$\PageIndex{2}$: Статично визначена система і розподіл згинального моменту.

Енергія деформації вигину становить

$$U(P) = \int_{0}^{l} \frac{1}{2EI} \left[ P^2 + \left(\frac{P}{2}\right)^2 + \left(\frac{P}{2}\right)^2 \right] x^2 dx = \frac{3}{2} P^2 \frac{l^3}{3} = \frac{1}{2} P^2 l^3$$

З відносного внеску трьох балок у Рівнянні (7.5.13) видно, що горизонтальна консоль вдвічі сприяє відхиленню наконечника порівняно з вертикальною балкою.

Малюнок$\PageIndex{3}$: дві зварні балки, що утворюють коліно.

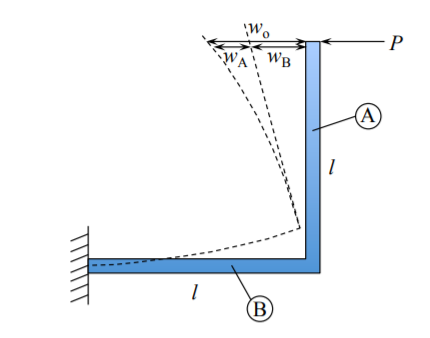
Друга система складається з ліктя. З малюнка ($\PageIndex{3}$) розподіл згинального моменту дорівнює

$$\text{ Beam (A) } \; M(x) = P x \\ \text{ Beam (B) } \; M(x) = Pl$$

Енергія пружного вигину системи становить

$$U(P) = \frac{1}{2EI} \int_{0}^{l} (P x)^2 dx + \frac{1}{2EI} \int_{0}^{l} (P l)^2 dx = \frac{P^2}{2EI} \frac{4l^3}{3}$$

Загальний прогин у напрямку сили дорівнює

$$w_o = \frac{dU}{dP} = \frac{4}{3} \frac{Pl^3}{EI}$$

Доказ теореми Кастільяно для системи точкових навантажень,$P_i$

Відповідні зсуви позначаються$w_i$, див. Малюнок ($\PageIndex{4}$).

Малюнок$\PageIndex{4}$: Пружне тіло (структура), навантажене системою зосереджених сил.

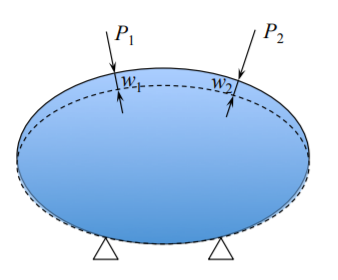
Робота зовнішніх сил - це

$$W = \sum_{i} P_iw_i = P_iw_i$$

Передбачається, що накопичена енергія може бути виражена в перерахунку на всі точкові сили,$U = U(P_i)$. Давайте збережемо всі точкові сили на фіксованих значеннях і варіюємо лише один, скажімо$P_k$. Для рівноваги сумарна потенційна енергія системи повинна бути нерухомою щодо цієї зміни. Таким чином,

$$\delta \prod = \delta (U - W) = \frac{dU}{dP_k} \delta P_k − w_k \delta P_k \\ = \left( \frac{dU}{dP_k} − w_k \right) \delta P_k = 0$$

Розширена теорема Кастільяно

$$w_k = \frac{\partial U(P_i)}{\partial P_k}$$

Наприклад, якщо застосовуються дві точкові навантаження,

$$w_2 = \frac{\partial U(P_1, P_2)}{\partial P_2}$$

Зазвичай теорема Кастільяно дає лише прогин у заданій точці, але не відхилену форму. Розширена теорема може бути використана для прогнозування відхиленої форми.

Малюнок$\PageIndex{5}$: Консольна балка навантажена двома точковими силами.

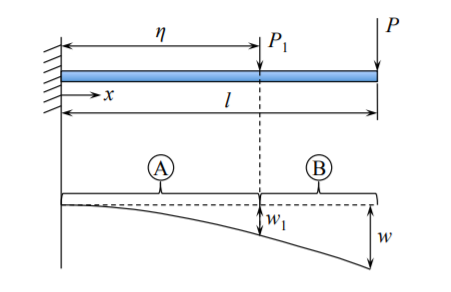
Ілюстрація

Розглянемо консольну балку, навантажену двома точковими силами. Одна сила$P$ прикладається на кінчику, а інша сила$P_1$ діє на відстані$\eta$ від опори.

Розподіл згинального моменту

$$\begin{array}{lcl} M_A(x) = P(l − x) + P_1(\eta − x) & \text{ for } & 0 < x < \eta \\ M_B(x) = P(l − x) & \text{ for } & \eta< x < l \end{array}$$

Енергія деформації вигину становить

$$U(P, P_1) = \frac{1}{2EI} \int_{0}^{\eta} M^2_{A} dx + \frac{1}{2EI} \int_{\eta}^{l} M^2_B dx$$

Згідно з рівнянням\ ref {8.49}, прогин під точковим навантаженням$P_1$ дорівнює

$$w_1 = \frac{\partial U(P, P_1)}{\partial P_1} = \frac{1}{EI} \int_{0}^{\eta} M_A \frac{\partial M_A}{\partial P_1} dx + \frac{1}{EI} \int_{\eta}^{l} M_B \frac{\partial M_B}{\partial P_1} dx$$

Похідними згинальних моментів є

$$\frac{\partial M_A}{\partial P_1} = \eta − x$$

$$\frac{\partial M_B}{\partial P_1} = 0$$

Підставляючи рівняння\ ref {8.51} і (?? ) в (?? ), один отримує

$$w_1 = \frac{1}{EI} \int_{0}^{\eta} [P(l − x) + P_1(\eta − x)](\eta − x) dx$$

Це рівняння справедливо для будь-якої комбінації$P$ і$P_1$. Тому ми можемо припустити, що$P_1$ це «фіктивна» сила і може бути встановлена рівною нулю. Тоді рівняння (?? ) зводить до

$$w_1 = \frac{1}{EI} \int_{0}^{\eta} [P(l − x)(\eta − x) dx$$

який дає, після інтеграції,

$$w_1(\eta) = \frac{Pl^3}{3EI} \left[ \frac{3}{2} \left(\frac{\eta}{l}\right)^2 − \frac{1}{2} \left(\frac{\eta}{l}\right)^3 \right]$$

У наведеному вище розчині$\eta$ знаходиться довільне положення уздовж балки і$w_1(\eta)$ є відповідним прогином. Змінюючи змінні

$$\eta \rightarrow x \\ w_1(\eta) = w(x)$$

ми можемо відновити точну відхилену форму консольної балки

$$w_1(\eta) = \frac{Pl^3}{3EI} \left[ \frac{3}{2} \left(\frac{x}{l}\right)^2 − \frac{1}{2} \left(\frac{x}{l}\right)^3 \right]$$

Наведений вище приклад проілюстрував велику гнучкість методу Кастільяно у вирішенні статично визначених задач.