7.1: Поняття потенційної енергії

З фізики середньої школи ви повинні згадати два рівняння

$$E = \frac{1}{2} Mv^2 \quad \text{ kinematic energy}$$

$$W = mgH \quad \text{ potential energy}$$

де$H$ - висота маси$m$ від певного еталонного рівня$H_o$, і$g$ позначає прискорення землі. Контрольним рівнем може бути центр землі, рівень моря або будь-яка поверхня, від якої$H$ вимірюється.

Малюнок$\PageIndex{1}$: Гравітаційна потенційна енергія.

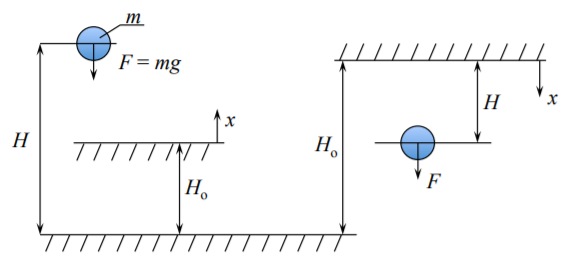
Ми рідко вимірюємо$H$ від центру землі. Тому те, що ми можемо легко виміряти, - це зміна потенційної енергії.

$$\Delta W = (mg)(H − H_o) \label{7.1.3}$$

Енергія завжди позитивна. Він може бути нульовим, але не може бути негативним. Сила тяжіння$F = mg$ спрямована до центру землі. Тому виникає необхідність у від'ємному знаку в Equation\ ref {7.1.3}). У системі координат Figure ($\PageIndex{1}$) сила тяжіння негативна (протилежна сенсу координати$x$). Сила$F$ діє в сенсі,$x$ але$H − H_o$ різниця негативна.

Розширюючи поняття потенційної енергії до променя, сила є$F = q dx$ і$w = H − H_o$ є прогин променя.

$$W \equiv + \int_{0}^{l} qw dx$$

Аналогічним виразом для пластин є

$$W \equiv + \int_{S} pw ds$$

Малюнок$\PageIndex{2}$: Потенційна енергія елемента променя і всього променя.

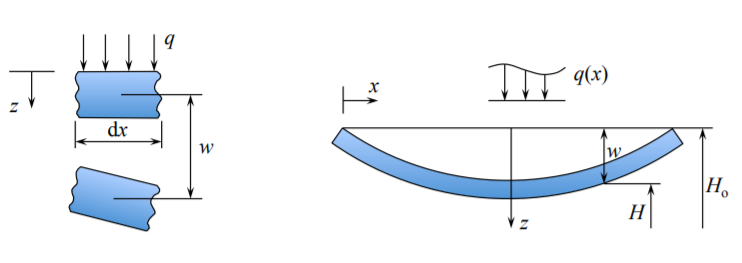
У вищенаведеному визначенні$W$ негативний.

Поняття енергії, що зберігається пружно,$U$ було введено раніше. Для 3-D тіла

$$U = \int_{V} \frac{1}{2} \sigma_{ij}\epsilon_{ij} dv$$

і для пучка

$$U = \int_{0}^{l} \frac{1}{2} MK dx + \int_{0}^{l} \frac{1}{2} N \epsilon^{\circ} dx$$

Для пластин енергії вигину і мембрани задаються рівняннями (3.6.25), (3.6.26) і (3.6.41), (3.6.42).

Загальна потенційна енергія$\prod$ - це нове поняття, і воно визначається як сума енергії стоку і потенційної енергії

$$\prod = U + (−W) = U − W$$

Враховуйте на час, що матеріал жорсткий, для чого$U \equiv 0$. Уявіть собі жорстку кульку, зміщену на нескінченно малу величину на плоскій$(\theta = 0)$ і похилій$(\theta \neq 0)$ поверхні, Рисунок ($\PageIndex{3}$).

Малюнок$\PageIndex{3}$: Перевірте, чи нескінченно мале зміщення$\delta u$ призводить до зміни потенційної енергії.

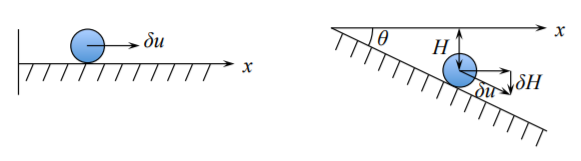
У нас є$H = u \sin \theta$ і$\delta H = \delta u \sin \theta$. Загальна потенційна енергія і її зміна

$$\prod = −W = −F u \sin \theta$$

$$\delta \prod = −\delta W = −(F \sin \theta) \delta u$$

На рівній поверхні$\theta = 0$ і$\delta \prod = 0$, і куля знаходиться в статичному (нейтральному) рівновазі. Якщо$\theta > 0$,$\delta \prod \neq 0$ і куля не знаходиться в статичній рівновазі. Зверніть увагу, що якщо додається сила інерції д'Аламбера в напрямку руху, м'яч все одно буде знаходитися в динамічній рівновазі. У цій лекції розглядається тільки статична рівновага. Тепер ми можемо розширити вищевказаний тест на рівновагу і ввести наступний принцип:

Система, як кажуть, знаходиться в рівновазі, якщо нескінченно мала зміна$a$ аргументу загальної потенційної енергії$\prod = \prod(a)$ не змінює загальну потенційну енергію

$$\delta \prod (a) = \frac{\partial \prod}{\partial a} \delta a = 0$$

Оскільки$\delta a \neq 0$ ($\delta a = 0$це банальний випадок, в якому не проводиться жодна перевірка на рівновагу) необхідною і достатньою умовою стійкості є

$$\frac{\partial \prod}{\partial a} = 0$$

У разі, коли функціонал$\prod$ є функцією багатьох (скажімо$N$) змінних$\prod = \prod(a_i)$, збільшення

$$\delta \prod = \frac{\partial \prod}{\partial a_i} \delta a_i, \quad i = 1, \dots, N$$

Система знаходиться в рівновазі, якщо похідна по відношенню до кожної змінної в той час зникає$\prod$

$$\frac{\partial \prod (a_i)}{\partial a_i} = 0, \quad i = 1, \dots, N$$

Значення аргументу (ів)$a_i$ або незалежних змінних буде пояснено далі.