Skip to main content
LibreTexts - Ukrayinska

10.5: Електрофлюїдика

  1. Last updated
  2. Save as PDF
  • Page ID
    29365

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    10.5.1.PNG
    Малюнок\(\PageIndex{1}\): Звужена труба, яка використовується для ілюстрації рівняння Бернуллі.

    Електрогідродинамічні пристрої (ЕХД) перетворюють між електричною енергією і потоком рідини. Ці пристрої також відомі як електрокінетичні пристрої. Мікрофлюїдні пристрої - це пристрої EHD, які нанесені малюнком на одній кремнієвій пластині або іншій підкладці, а шкали довжини часто менше міліметра [159]. Інженери побудували EHD насоси, клапани, змішувачі, сепаратори та інші пристрої EHD [159] [160]. Електрогідродинамічні або мікрорідинні пристрої використовувалися в продуктах, включаючи струменеві принтери, хімічні детектори, машини для секвенування ДНК або аналізу білка, а також інсулінові насоси [61] [160] [161].

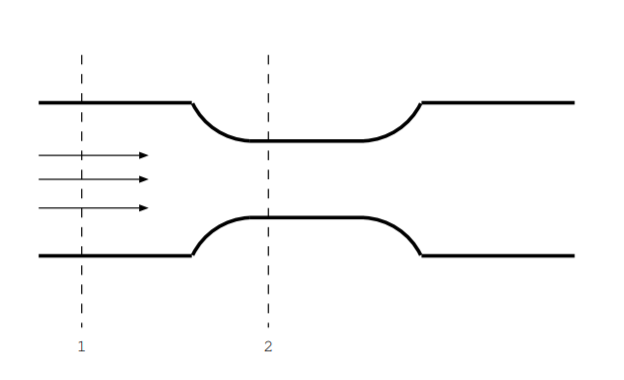
    Деякі пристрої EHD працюють на основі ідеї рівняння Бернуллі, і цей зв'язок є прямим наслідком енергозбереження. Щоб проілюструвати фундаментальну фізику цієї ідеї, почніть з розгляду більш простого пристрою, звуженої труби. Ця труба перетворює енергію з перепаду тиску в кінетичну енергію [103, гл. 3] [162, с. 346]. Розглянемо рідину з нульовою в'язкістю і нульовою теплопровідністю, що протікає по горизонтальній трубі (так гравітацію можна ігнорувати). Малюнок\(\PageIndex{1}\) ілюструє цю геометрію. Швидкість\(\overrightarrow{v}\) і тиск\(\mathbb{P}\) різні в місцях з різним діаметром труби, наприклад місця 1 і 2 на малюнку. Розглянемо невелику кількість води з масою\(m = \rho_{dens} \Delta \mathbb{V}\)\(\rho_{dens}\), де\(\Delta \mathbb{V}\) щільність і невеликий обсяг. Припустимо, що існує дві, і тільки дві, складові енергії: кінетична енергія і енергія за рахунок стисненої рідини. При переході від місця 1 до місця 2 тиск цієї невеликої маси рідини змінюється. Зміна енергії за рахунок стиснення цієї краплі води дорівнює\((\mathbb{P}_1 - \mathbb{P}_2) \Delta \mathbb{V}\). Кінетична енергія також змінюється, а зміна кінетичної енергії задається

    \[\frac{1}{2} m|\overrightarrow{v_{1}}|^{2}-\frac{1}{2} m|\overrightarrow{v_{2}}|^{2}=\frac{1}{2}\left(\rho_{\text {dens}} \Delta \mathbb{V}\right)\left(|\overrightarrow{v_{1}}|^{2}-|\overrightarrow{v_{2}}|^{2}\right). \nonumber \]

    Однак енергія зберігається, тому

    \[\left(\mathbb{P}_{1}-\mathbb{P}_{2}\right) \Delta \mathbb{V}+\frac{1}{2}\left(\rho_{\text {dens}} \Delta \mathbb{V}\right)\left(|\overrightarrow{v_{1}}|^{2}-|\overrightarrow{v_{2}}|^{2}\right)=0. \nonumber \]

    Цей вираз можна спростити алгебраїчно.

    \[\mathbb{P}_{1}-\mathbb{P}_{2}+\frac{1}{2} \rho_{\text {dens}}\left|\vec{v}_{1}\right|^{2}-\frac{1}{2} \rho_{\text {dens}}\left|\vec{v}_{2}\right|^{2}=0 \nonumber \]

    І тиск,\(\mathbb{P}\) і швидкість\(\overrightarrow{v}\) є функціями розташування. Єдиний спосіб, яким цей вираз може бути вірним для всіх локацій, це якщо воно вірно для кожного місця і константа.

    \[\mathbb{P}_{1}+\frac{1}{2} \rho_{\text {dens}}|\overrightarrow{v_{1}}|^{2}=\mathbb{P}_{2}+\frac{1}{2} \rho_{\text {dens}}|\overrightarrow{v_{2}}|^{2}=\text { constant } \nonumber \]

    Рівняння Бернуллі з досить суворими припущеннями вище стає

    \[\mathbb{P}+\frac{1}{2} \rho_{\text {dens}}|\vec{v}|^{2}=\text { constant }. \label{10.5.5} \]

    Рівняння Бернуллі також використовується для опису підйому повітряної фольги або шляху кривого м'яча в бейсболі [162, с. 350]. У деяких ЕХД електрика індукує зміни тиску або обсягу мікрорідинного каналу. Рідина в цих пристроях може бути струмопровідною або ізолюючої. Як видно з Equation\ ref {10.5.5}, ця зміна тиску викликає зміну швидкості рідини.

    В інших ЕХД прикладені напруги чинять сили на струмопровідні рідини. Заряджений об'єкт у зовнішньому електричному полі\(\overrightarrow{E}\) відчуває силу в напрямку електричного поля. Струм у зовнішньому магнітному полі\(\overrightarrow{B}\) відчуває силу. Напрямок цієї сили перпендикулярно як напрямку струму, так і напрямку зовнішнього магнітного поля. Ці ефекти узагальнені рівнянням сили Лоренца

    \[\overrightarrow{F} = Q \left( \overrightarrow{E} +\overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \]

    про який йшлося в главі 5. У цьому розділі обговорювалися пристрої ефекту Холла та магнітогідродинамічні пристрої, обидва з яких можна зрозуміти за рівнянням сили Лоренца із зовнішнім магнітним полем, але без електричного поля. Цей тип ЕГД можна зрозуміти за рівнянням сили Лоренца із зовнішнім електричним полем, але без магнітного поля. Рідина в цих приладах повинна бути струмопровідною. Коли напруга подається на цей тип ЕHD, індукується електричне поле, яке змушує рідину текти, і цей ефект, як кажуть, обумовлений потоковим потенціалом [159]. Пов'язаний ефект під назвою електрофорез виникає в рідинях, які містять заряджені частинки [161]. Якщо застосувати електричне поле, ці частинки будуть рухатися. Цей ефект був продемонстрований із зарядженими молекулами ДНК та зарядженими молекулами білка в розчині [161].

    Інші пристрої EHD працюють шляхом зміни поляризації матеріалу ізолюючої рідини, і цей ефект називається діелектрофорезом. Поняття поляризації матеріалу обговорювалося в розділі 2.2.1. Якщо ми застосуємо електричне поле на провідник, незалежно від того, чи є цей провідник твердим або рідиною, заряди будуть текти. Якщо застосувати електричне поле через діелектрик, матеріал може поляризуватися. Іншими словами, буде деякий зміщення чистого заряду, навіть якщо всі електрони залишаться пов'язаними з атомами. Зовнішнє електричне поле змушує як атоми рідини поляризуватися, так і ці поляризовані атоми течуть.

    Існує ряд інших взаємопов'язаних ефектів ЕГД. Електроосмоз може виникати в рідинях з поверхневим зарядом. У деяких рідинях іони накопичуються на поверхні через непарних хімічних зв'язків, через іонів, адсорбованих на поверхні, або з інших причин. Якщо через цей шар зарядів накласти електричне поле, то рідина буде текти, і цей ефект називається електроосмосом [161] [159]. Крім того, зовнішнє електричне поле, нанесене на рідину, може нагріти частину рідини і викликати градієнт температури. Рідина може текти через температурного градієнта, і цей ефект називається електротермічним потоком [161]. Інший ефект, відомий як електрозмочування, виникає в провідних рідинях. На межі розділу твердого провідника і струмопровідної рідини накопичуються заряди [61]. Знову ж таки, якщо застосувати електричне поле, рідина буде текти.