6.3: Переглянуто кристалографію
- Page ID
- 29500
Реальний простір і взаємний простір
Фізики та хіміки часто цікавляться, де електрони або нуклони атомів, ймовірно, можна знайти щодо положення в реальному просторі. Ідеї решітки, основи та кристалічної структури обговорювалися в п. 2.3.2. Для огляду решітка описує розташування точок. Основа описує, як атоми розташовані в кожній точці решітки. Решітка і основа разом утворюють кристалічну структуру. 3D решітка описується трьома гратчастими векторами\(\overrightarrow{a_1}\)\(\overrightarrow{a_2}\), і\(\overrightarrow{a_3}\). Якщо їх вибрати максимально короткі, то їх називають примітивними гратчастими векторами. Величина вектора примітивної решітки може бути близько 0,1 нм. Примітивні вектори решітки визначають комірку, яка називається примітивною коміркою. Оскільки решітка періодична, якщо ми знаємо, як описати одну примітивну клітинку, ми можемо описати всю решітку.
Для кожної решітки існує відповідна зворотна решітка, визначена набором векторів. Обидва містять одну і ту ж інформацію в різних формах. Для 3D решітки з примітивними векторами\(\overrightarrow{a_1}\)\(\overrightarrow{a_2}\)\(\overrightarrow{a_3}\), і, вектори зворотної решітки позначені векторами\(\overrightarrow{b_1}\)\(\overrightarrow{b_2}\), і\(\overrightarrow{b_3}\).
\[\overrightarrow{b_1} = \frac{2 \pi \overrightarrow{a_2} \times \overrightarrow{a_3}}{\overrightarrow{a_1} \cdot \overrightarrow{a_2} \times \overrightarrow{a_3}} \nonumber \]
\[\overrightarrow{b_2} = \frac{2 \pi \overrightarrow{a_3} \times \overrightarrow{a_1}}{\overrightarrow{a_1} \cdot \overrightarrow{a_2} \times \overrightarrow{a_3}} \nonumber \]
\[\overrightarrow{b_3} = \frac{2 \pi \overrightarrow{a_1} \times \overrightarrow{a_2}}{\overrightarrow{a_1} \cdot \overrightarrow{a_2} \times \overrightarrow{a_3}} \nonumber \]
Зверніть увагу,\(\overrightarrow{b_1}\) що перпендикулярно\(\overrightarrow{a_2}\) і\(\overrightarrow{a_3}\). Крім того\(\overrightarrow{b_1}\), паралельно\(\overrightarrow{a_1}\). Більш конкретно,\( |\overrightarrow{b_1}| \cdot |\overrightarrow{a_1}| = 2 \pi\). (Фактори\(2 \pi \) показу через вибір одиниць,\(\frac{cycles}{m}\) проти\(\frac{rad}{m}\).) Таким чином,\(\overrightarrow{a_1}\) якщо вектор довгий,\(\overrightarrow{b_1}\) буде коротким. Так само, як ми можемо отримати від однієї точки решітки до іншої шляхом переміщення цілих кратних векторів\(\overrightarrow{a_\mathfrak{n}}\) решітки, ми можемо отримати від будь-якої точки до наступної зворотної решітки шляхом переміщення цілих кратних вектора\(\overrightarrow{b_\mathfrak{n}}\) решітки. Вектори решітки в реальному просторі мають одиниці довжини,\(m\). Вектори решітки у зворотному просторі мають одиниці виміру\(m^{-1}\).
Зворотна решітка дає інформацію про просторовій частоті атомів. Якщо площини атомів в кристалі тісно розташовані в одному напрямку,\(|\overrightarrow{a_1}|\) це відносно мало. Відповідний зворотний вектор\(|\overrightarrow{b_1}|\) відносно великий. Зворотна решітка представляє просторову частоту атома в одиницях\(m^{-1}\). Якщо площини атомів у кристалі знаходяться далеко один від одного,\(|\overrightarrow{a_1}|\) є великим і\(|\overrightarrow{b_1}|\) малим.
Якщо промінь світла світить на кристал, де довжина хвилі світла близька до відстані кристалів, світло буде дифраговано, а дифракційна картина пов'язана з зворотною решіткою. Зона Бріллуена - примітивна клітина для зворотної решітки. Обсяг одиничної комірки у зворотному просторі над одиничною коміркою в реальному просторі задається
\[\frac{\text{vol. Brillouin zone}}{\text{vol. primitive cell in real space}} = \frac{\overrightarrow{b_1} \cdot \overrightarrow{b_2} \times \overrightarrow{b_3}}{\overrightarrow{a_1} \cdot \overrightarrow{a_2} \times \overrightarrow{a_3}} =(2\pi)^3. \nonumber \]
Що стосується реальної космічної решітки, то для розуміння зворотної космічної решітки нам потрібно розуміти лише одну клітинку, оскільки зворотна космічна решітка є періодичною.
проти k діаграм
Діаграми енергетичного рівня, розглянуті в розділі 6.2, будують дозволені енергії електронів там, де вертикальна вісь представлена енергія. На горизонтальній осі не показано жодних змін. Найбільш корисні діаграми енергетичного рівня для напівпровідників збільшені таким чином, що відображаються лише валентна та провідна смуга. У багатьох випадках корисно будувати діаграми рівня енергії проти положення в реальному просторі. Для такої діаграми вертикальна вісь представляє енергію, а горизонтальна вісь - положення. Також корисно будувати діаграми рівня енергії в порівнянні з положенням у взаємному просторі.
Кінетична енергія задається
\[E_{kinetic} = \frac{1}{2}m|\overrightarrow{v}|^2 = \frac{1}{2m}|\overrightarrow{M}|^2 \nonumber \]
де\(\overrightarrow{v}\) представляє швидкість в\(\frac{m}{s}\) і\(m\) представляє масу в кг. Імпульс задається\(\overrightarrow{M} = m\overrightarrow{v}\) в одиницях\(\frac{kg \cdot m}{s} = \frac{J \cdot s}{m}\). Електрони в кристалах при\(T > 0\) К вібрують, а певні коливання резонансні в кристалі. Кристал імпульс\(\overrightarrow{M}_{crystal}\) являє собою внутрішній імпульс за рахунок вібрацій. Вона може виражатися як
\[\overrightarrow{M}_{crystal} = \hbar\overrightarrow{k} \nonumber \]
і має одиниці імпульсу\(\frac{kg \cdot m}{s}\). Величина\(\overrightarrow{k}\) називається хвильовим вектором, і вона має одиниці\(m^{-1}\). Він являє собою зміну просторової частоти, відстані у зворотному просторі. Постійна
\[\hbar = \frac{h}{2\pi} \nonumber \]
називається h-bar і є постійною Планка розділена на\(2\pi\). Кінетичну енергію можна записати через хвильовий вектор.
\[E_{kinetic} = \frac{\hbar^2 |\overrightarrow{k}|^2}{2m} \label{6.3.8} \]
Рівняння\ ref {6.3.8} описує, як енергія електрона змінюється залежно від хвильового вектора\(|\overrightarrow{k}|\), який містить інформацію про коливання решітки. Енергія квадратична в хвильовому векторі, тому ділянки енергії проти\(|\overrightarrow{k}|\) параболічні. Рівняння\ ref {6.3.8} є лише моделлю, і вона найкраще застосовується у верхній частині валентної зони та знизу зони провідності.
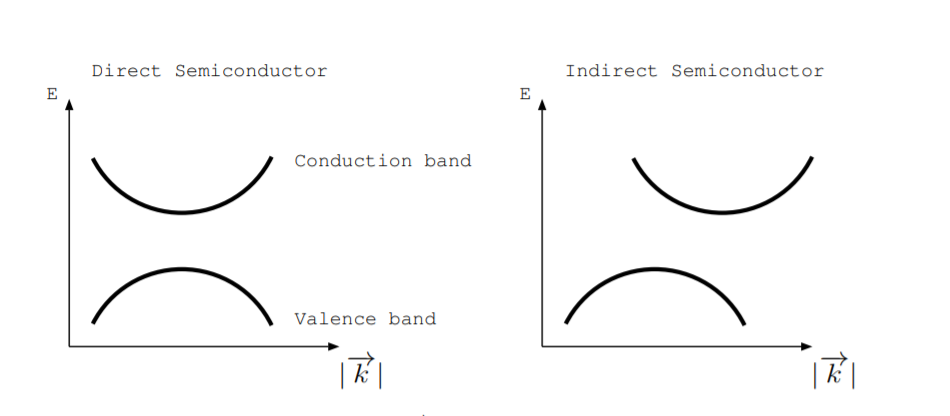
Енергія проти\(|\overrightarrow{k}|\) діаграм графіка дозволених рівнів енергії. Подумайте про\(|\overrightarrow{k}|\) вісь як про зміну положення у взаємному просторі. Якщо верхня частина валентної зони і нижня частина зони провідності відбуваються при однаковому\(|\overrightarrow{k}|\) значенні в напівпровіднику, ми говоримо, що вона пряма. Якщо верхня частина валентної зони і нижня частина зони провідності відбуваються при різних\(|\overrightarrow{k}|\) значеннях, ми говоримо, що напівпровідник непрямий. Ліва частина рис. \(\PageIndex{1}\)показує енергію проти\(|\overrightarrow{k}|\) діаграми для прямого напівпровідника, а права частина рис. \(\PageIndex{1}\)показує один для непрямого напівпровідника. GaAs, InP і ZnTe є прямими напівпровідниками. Si, Ge, AlAs і GaP - це непрямі напівпровідники. Уздовж різних кристалічних осей дещо змінюється смугова структура. Горизонтальна вісь енергія проти\(|\overrightarrow{k}|\) діаграми може бути вказана вздовж певної осі у зворотному просторі.
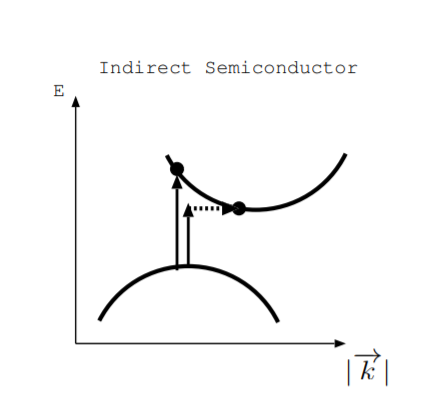
Що відбувається, коли ми світимо світло на прямий напівпровідник? Фотон достатньої енергії може збуджувати електрон з валентної зони в зону провідності для створення пари електрон-дірка. Що відбувається в непрямому напівпровіднику? Малюнок\(\PageIndex{2}\) ілюструє дві можливості. Як ілюструє довша стрілка, електрон може збуджуватися безпосередньо від валентної до зони провідності. Однак для цього потрібен фотон більшої енергії, ніж вертикальна відстань між вершиною валентної зони і дном зони провідності [25, с. 200]. Як варіант, як ілюструють інші дві стрілки, збудження від верхньої частини валентної зони до нижньої частини смуги провідності може включати фотон і фонон. І енергія, і імпульс повинні бути збережені, тому зміна імпульсу кристала необхідна для збудження електрона в цьому випадку. Сонячні елементи та фотоприймачі можуть бути виготовлені як з прямих, так і з непрямих напівпровідників.
