2.4: Проблеми

2.1. Паралельний пластинчастий конденсатор має ємність\(C =10 pF\). Пластини мають площу\(0.025 cm^2\). Діелектричний шар товщини\(d_{thick} = 0.01 mm\) відокремлює пластини. Для діелектричного шару обчислити діелектричну проникність\(\epsilon\), відносну діелектричну\(\epsilon_r\) проникність та електричну сприйнятливість\(\chi_e\).

2.2. Ми часто припускаємо, що ємність конденсатора і діелектрична проникність матеріалу є постійними. Однак іноді ці величини краще описувати як функції частоти. Розглянемо конденсатор, виготовлений з паралельних пластин площею,\(0.025 cm^2\) розділеної на\(0.01 mm\). Припустимо\(\omega \lesssim 10^6 \frac{rad}{s}\), що для, ємність добре моделюється\[C(\omega) = 8 \cdot 10^{-11} + 3 \cdot 10^{-15} \omega \nonumber \] в фарад. Для діелектричного матеріалу між обкладинками конденсатора обчислити діелектричну проникність\(\epsilon(\omega)\), відносну діелектричну\(\epsilon_r(\omega)\) проникність та електричну сприйнятливість\(\chi_e(\omega)\).

2.3. Циліндричне сендвіч-печиво має радіус 0,75 дюйма. Печиво виготовляється з двох вафель, кожна товщиною 0,15 дюйма, які є ідеальними діелектриками відносної діелектричної проникності\(\epsilon_r =2.8\). Між вафлями знаходиться шар кремової начинки товщиною 0,1, в якому знаходиться ідеальний діелектрик відносної діелектричної проникності\(\epsilon_r =2.2\). Знайдіть загальну ємність печива. Підказка: Ємності послідовно поєднуються як\(\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}}\).

2.4. Паралельний пластинчастий конденсатор має ємність\(3 \mu F\).

(а) Припустимо, що інший конденсатор виготовлений з використанням того ж діелектричного матеріалу і з однаковою площею поперечного перерізу. Однак товщина діелектрика між обкладинками конденсатора вдвічі більше, ніж у вихідного конденсатора. Яка його ємність?

(b) Припустимо, що третій конденсатор виготовлений з тією ж площею перерізу і товщиною, що і перший конденсатор, але з матеріалу з подвоєною діелектричною проникністю. Яка його ємність?

2.5. П'єзоелектричний матеріал має діелектричну проникність\(\epsilon = 3.54 \cdot 10^{-11} \frac{F}{m}\) і має п'єзоелектричну константу деформації\(d =2 \cdot 10^{-10} \frac{m}{V}\). Якщо матеріал поміщений в електричне поле міцності\(|\overrightarrow{E}| =70 \frac{V}{m}\) і піддається напруженню\(|\overrightarrow{\varsigma}| =3.5 \frac{N}{m^2}\). Обчисліть поляризацію матеріалу.

2.6. П'єзоелектричний матеріал має діелектричну проникність\(\epsilon_r = 2.5\). Якщо матеріал поміщений в електричне поле міцності\(|\overrightarrow{E}| =2\cdot10^3\frac{V}{m}\) і піддається напруженню\(|\overrightarrow{\varsigma}| =200 \frac{N}{m^2}\), матеріал поляризації матеріалу є\(3.2 \cdot 10^{-8} \frac{C}{m^2}\). Обчисліть\(d\), п'єзоелектричну константу деформації.

2.7. Розглянемо два п'єзоелектричних пристрою однакового розміру і форми. Діелектричний матеріал першого пристрою має діелектричну проникність\(\epsilon = 2.21 \cdot 10^{-11} \frac{F}{m}\) і п'єзоелектричну деформаційну константу\(d = 8 \cdot 10^{-11} \frac{m}{V}\). Діелектричний матеріал другого пристрою має електричну сприйнятливість\(chi_e =3.2\) і п'єзоелектричну деформаційну константу\(d = 2 \cdot 10^{-10} \frac{m}{V}\).

(а) Знайдіть\(\epsilon_r\) відносну діелектричну проникність для кожного пристрою.

(б) Знайти\(\frac{C_1}{C_2}\), відношення ємності першого пристрою до ємності другого пристрою.

(c) Пристрої розміщуються у зовнішньому електричному полі напруженості\(|\overrightarrow{E}| =32 \frac{V}{m}\). Ніяких навантажень на пристрої не ставиться. Розрахуйте поляризацію матеріалу,\(\overrightarrow{P}\) для кожного пристрою.

(d) Пристрої розміщуються у зовнішньому електричному полі сили\(|\overrightarrow{E}| =32 \frac{V}{m}\), і напруга\(|\overrightarrow{\varsigma}| =100 \frac{N}{m^2}\) прикладається до пристроїв. Розрахуйте поляризацію матеріалу,\(\overrightarrow{P}\) для кожного пристрою.

(e) Який пристрій ви очікуєте, здатний зберігати більше енергії? Поясніть свою відповідь.

2.8. Конкретний п'єзоелектричний пристрій має площу поперечного перерізу\(10^{-5} m^2\). Коли\(800 \frac{N}{m^2}\) накладається стрес, пристрій стискає повз\(10 \mu m\). У цих умовах пристрій може генерувати\(2.4 \cdot 10^{-9} J\). Розрахуйте ККД приладу.

2.9. Конкретний п'єзоелектричний пристрій має площу поперечного перерізу\(10^{-5} m^2\) і ККД 5%. Коли на пристрій\(1640 \frac{N}{m^2}\) прикладається напруга, він коливається із середньою швидкістю\(0.01 \frac{m}{s}\). Розрахуйте потужність, яку можна генерувати від приладу.

2.10. П'єзоелектричний пристрій поміщають в електричне поле напруженості\(|\overrightarrow{E}| =500 \frac{V}{m}\). Пристрій тестується двічі. У першому тесті напруга\(|\overrightarrow{\varsigma}| =1000 \frac{N}{m^2}\) була поставлена на пристрій, і поляризація матеріалу вимірювалася, щоб бути\(|\overrightarrow{P}| =2.75 \cdot 10^{-8} \frac{C}{m^2}\). У другому тесті також з\(|\overrightarrow{E}| =500 \frac{V}{m}\), напруга\(|\overrightarrow{\varsigma}| =100 \frac{N}{m^2}\) була поставлена на пристрій, і поляризація матеріалу вимірювалася бути\(|\overrightarrow{P}| =6.50 \cdot 10^{-9} \frac{C}{m^2}\). Знайдіть постійну п'єзоелектричної\(d\) деформації та знайдіть відносну діелектричну проникність матеріалу\(\epsilon_r\).

2.11. Згідно з технічним паспортом, п'єзоелектричний пристрій є ефективним на 3%. Співробітник каже, що енергія не зберігається в пристрої, оскільки 97% енергії втрачається при її використанні. Поясніть, що не так з поясненням вашого колеги.

2.12. Зіставте властивість матеріалу з його визначенням. (Не всі визначення будуть використані.)

1. Механічне напруження спричинить (матеріальну) поляризацію в цьому типі матеріалу.	А. аморфний
2. Цей тип матеріалу є склоподібним і некристалічним.	B. Діелектрик
3. Заряди не легко протікають через цей тип матеріалу	C. Сегнетоелектричні
4. При наявності слабкого зовнішнього напруги заряди в даному виді матеріалу не надходять. При наявності сильного зовнішнього напруги заряди протікають легко.	D. п'єзоелектричний
5. Поляризація матеріалу в одному атомі індукує поляризацію матеріалу в сусідніх атомах цього типу матеріалу.

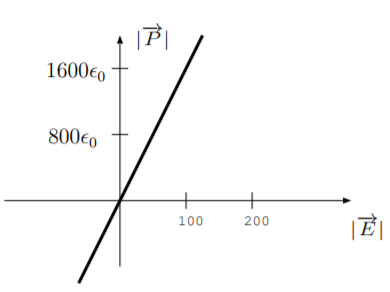
2.13. Розглянемо п'єзоелектричний матеріал у зовнішньому електричному полі\(\overrightarrow{E}\) в одиницях V м На малюнку показана величина поляризації матеріалу\(\frac{C}{m^2}\),\(|\overrightarrow{P}|\) в одиницях, як функція напруженості зовнішнього електричного поля при відсутності механічних навантажень. Матеріал має п'єзоелектричну постійну деформації\(d = 5 \cdot 10^{-10} \frac{m}{V}\).

(а) Знайдіть відносну діелектричну\(\epsilon_r\) проникність та знайдіть електричну сприйнятливість\(\chi_e\).

(b) Знайти та побудувати вираз для величини поляризації матеріалу як функції напруженості зовнішнього електричного поля при\(1000 \frac{N}{m^2}\) застосуванні напруги. Добре позначте осі вашої ділянки.

(c) Цей матеріал використовується для виготовлення п'єзоелектричного пристрою з площею поперечного перерізу\(1 cm^2\). Коли цей пристрій стискається на відстані\(1 mm\),\(2 \cdot 10^{-10} J\) накопичується енергія. Знайдіть ККД приладу.

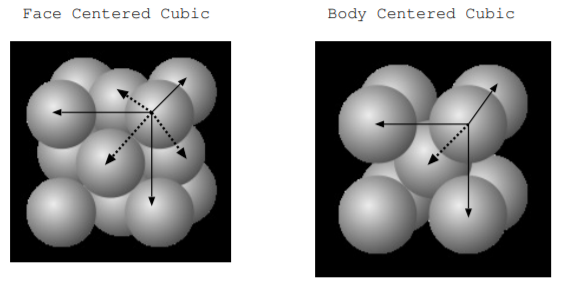
2.14. Розглянемо 2D кристалічну структуру, показану на малюнку, складену з решітки і кристалічної основи. Кристалічна основа складається з двох атомів типу А і одного атома типу В.

(а) Намалюйте кришталеву основу.

(б) Намалюйте 2D решітку.

(c) Намалюйте два примітивні вектори\(\overrightarrow{a}_1\) і\(\overrightarrow{a}_2\) на вашому ескізі.

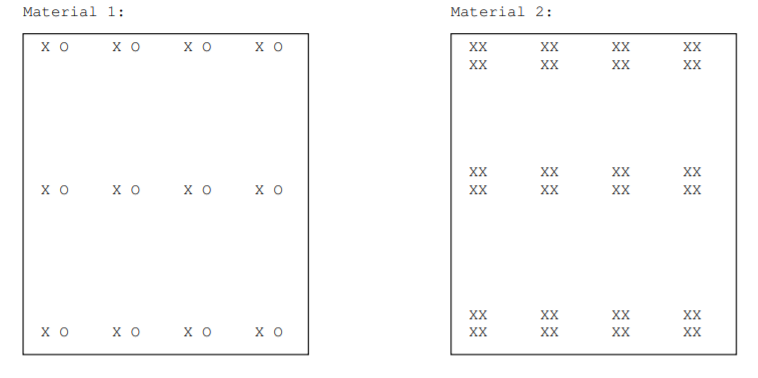
2.15. Розглянемо ілюстрації кристалічної структури двох 2D матеріалів, де X і O представляють розташування різних типів атомів. Чи мають матеріали однакову кристалічну структуру? основа? решітки? кришталева точка групи? Відповідайте так чи ні, і поясніть.

2.16. На малюнку нижче зображені дві можливі кристалічні решітки: кубічна решітка, центрована по грані, і кубічна решітка, центрована по тілу. Тверді стрілки представляють вектори решітки, але не примітивні вектори решітки, а показані осередки не є примітивними клітинами. Пунктирні вектори на малюнку показують примітивні вектори решітки. У випадку кубічної решітки, орієнтованої на грань, примітивні вектори решітки йдуть від кутової точки до точки посередині однієї з граней куба. У кубічній решітці з центром тіла примітивні вектори решітки йдуть від кутової точки до точки в центрі комірки, що межує з цим кутом. Припустимо, що тверді вектори мають довжину 0,4 нм. Знайти довжину вектора примітивної решітки в грані центрованої кубічної решітки, і знайти довжину примітивного вектора решітки в тілі центрованої кубічної решітки.