3.8: Інвертори та логіка

Last updated
Save as PDF

Page ID: 34467

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Як ви вже знаєте, або незабаром дізнаєтеся, починаючи з класу цифрової логіки, логічні схеми в першу чергу засновані на схемі, яка називається інвертором. Інвертор просто приймає сигнал і видає вам протилежний. Наприклад, якщо висока напруга («одиниця») розміщується на вході інвертора, вона повертає низьку напругу («нуль»). Малюнок\(\PageIndex{1}\) являє собою простий інвертор на базі MOSFET транзистора:

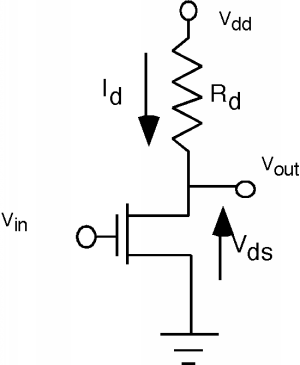MOSFET має напругу V_in подається на його затвор і його джерело заземлений. Злив підключений до резистора R_d, дальній кінець якого має напругу V_DD, а ближній кінець має напругу V_dS. Струм i_D протікає через резистор до MOSFET.

Якщо\(V_{\text{in}}\) дорівнює нулю, то MOSFET вимкнений (\(V_{\text{gs}} < V_{T}\)) і тому через резистор не протікає струм\(V_{\text{out}} = V_{\text{dd}}\), причому, високий. Якщо\(V_{\text{in}}\) високий (і ми припускаємо, що\(V_{T}\) для MOSFET значно менше\(V_{\text{in}}\)), то транзистор включений, а якщо\(R\) і\(\frac{W}{L}\) вибираються так, щоб через нього протікає достатня кількість струму,\(R\) щоб скинути більшу частину\(V_{\text{dd}}\) через нього, то\(V_{\text{out}}\) буде низьким.

Зазвичай це описується через функцію передачі, яка говорить нам, що вихідна напруга як функція вхідної напруги. Давайте відвернемося всього на хвилину і подивимося, як така функція може бути досягнута. Озираючись назад на\(\PageIndex{2}\) Малюнок, повинно бути легко побачити, що\[V_{\text{dd}} = I_{d} R_{d} + V_{\text{ds}}\]

Ми можемо переписати це як рівняння для\(I_{d}\). \[I_{d} = \frac{V_{\text{dd}}}{R_{d}} - \frac{V_{\text{ds}}}{R_{d}}\]

Це називається рівнянням лінії навантаження. Він говорить, що\(I_{d}\) змінюється лінійно з\(V_{\text{ds}}\) (з негативним нахилом) і має вертикальне зміщення\(\frac{V_{\text{dd}}}{R_{d}}\). Припустимо, у нас є транзистор MOSFET, для якого ми вже побудували характерні криві в попередньому графіку. Ми пустимо\(V_{\text{dd}} = 5 \mathrm{~Volts}\), і нехай\(R_{d} = 1 \mathrm{~k} \Omega\). З Рівняння\(\PageIndex{2}\) ми бачимо\(V_{\text{ds}} = 0\), що коли\(5 \mathrm{~mA}\),\(I_{d}\) буде і коли\(V_{\text{ds}} = V_{\text{dd}}\),\(I_{d}\) буде\(0\). Потім це дає нам пряму лінію на характерній кривій графіку, яка називається лінією навантаження. Це показано на малюнку\(\PageIndex{2}\).

Графік з осями I_DS в міліамперах і V_dS в вольтах, що показує характеристичні криві MOSFET для значень V_GS від 2 до 7 і лінію навантаження, що проходить між точками v_DD = 5 на осі x і v_DD/R_D = 5 на осі y. — Малюнок\(\PageIndex{2}\): Характеристичні криві з лінією навантаження

Озираючись назад на схему для інвертора на малюнку\(\PageIndex{1}\), ми бачимо, що один і той же струм\(I_{d}\) протікає через навантажувальний резистор\(R_{d}\) і через транзистор. Таким чином, правильне значення струму і напруги для ланцюга при будь-якому заданому напрузі затвора - це одночасне рішення рівняння лінії навантаження і поведінки транзистора, яке, звичайно, є якраз перетином лінії навантаження з відповідною характеристичною кривою. Таким чином, це проста справа малювання вертикальних ліній вниз від кожної\(V_{\text{in}}\) кривої або\(V_{\text{gs}}\) значення вниз до горизонтальної осі, щоб з'ясувати, яка відповідна\(V_{\text{dd}}\) або вихідна напруга буде для інвертора. Якщо припустити, що йде\(V_{\text{in}}\) тільки до 5 вольт, отримана крива, яку ми отримуємо, виглядає як рис\(\PageIndex{3}\). Це не велика характеристика передачі. \(V_{\text{in}}\)повинен отримати досить великий, перш ніж\(V_{\text{out}}\) почне падати, і навіть при повному 5-вольтовому вході, все\(V_{\text{out}}\) одно більше 1 вольт. Вибір транзистора з малим\(V_{T}\) і більшим резистором навантаження дасть нам кращу реакцію, але принаймні з цим прикладом ви можете побачити, що відбувається.

Малюнок\(\PageIndex{3}\): Передача характеристик для схеми інвертора.

Графік V_out проти V_in. Графік приймає форму горизонтальної лінії при V_out = 5 для значень v_in від 0 до 2, потім плавно переходить у зворотну S-форму, яка закінчується на V_out = 1.5 при значенні v_in 5. — Малюнок\(\PageIndex{3}\): Передача характеристик для схеми інвертора.

На основі цієї простої схеми інвертора ми можемо побудувати схеми, які виконують функції NOR і NAND. \[C_{\text{out}} = \neg \ (A+B)\]

і\[C_{\text{out}} = \neg \ (AB)\]

На даний момент вам повинно бути очевидним, як дві схеми на малюнку\(\PageIndex{4}\) можуть виконувати функцію NAND та NOR. Виявляється, що з можливістю робити NAND і NOR, ми можемо створити будь-яку логічну функцію, яку ми хочемо.

Малюнок\(\PageIndex{4}\): Ланцюги NAND і NOR

Ланцюг NAND складається з одного МОП-транзистора з затвором B, заземленого джерела та стоку, підключеного до джерела другого МОП-транзистора з затвором А. МОП-транзистор має стік, підключений до резистора, причому напруга на ближньому боці резистора позначається C_Out і напруга на дальній стороні позначено v_DD. Схема NOR моделюється як MOSFET із затвором A, заземленим джерелом, і стоком, який веде до переходу з однією гілкою, що містить резистор з напругою v_DD на дальній стороні, а інша гілка, що з'єднується зі стоком другого МОП-транзистора із затвором B і заземленим джерелом. Напруга, прийняте на стоці B MOSFET, маркується C_out. — Малюнок\(\PageIndex{4}\): Ланцюги NAND і NOR

Давайте розглянемо інвертор трохи докладніше. Зазвичай навантаження для інвертора буде наступним етапом логіки, який разом з пов'язаною з нею міжконнекторної проводкою ми можемо моделювати як простий конденсатор. Значення ємності буде варіюватися, але воно буде на порядок\(10^{-12} \mathrm{~F}\).

Малюнок\(\PageIndex{5}\): Схема ємнісного навантаження

MOSFET має постійну напругу, прикладену до його затвора протягом періоду часу t Його джерело заземлений, а його стік веде до переходу з однією гілкою, що веде до резистора R, який має напругу v_dd на дальньому кінці, а інша гілка, що веде до конденсатора C, дальній кінець якого заземлений. Вихідна напруга, зчитується після переходу і перед конденсатором, різко зростає відразу після періоду часу t і в кінцевому підсумку вирівнюється. — Малюнок\(\PageIndex{5}\): Схема ємнісного навантаження

Коли вхід в інвертор миттєво перемикається на низьке значення, струм перестане протікати через транзистор, а замість цього почне заряджати ємність навантаження. Вихідна напруга буде слідувати звичайній кривій\(\mathrm{RC}\) зарядки з постійною часу, що задається лише добутком\(R\) разів\(C\). Якщо\(C\) є\(10^{-13} \mathrm{~F}\), то, щоб отримати час підйому,\(1 \mathrm{~ns}\) ми повинні були б зробити\(R\) про\(10^{4} \ \Omega\).

Як ми побачимо далі, зробити\(10 \mathrm{~k} \Omega\) резистор за допомогою методів інтегральних схем практично неможливо. Запам'ятайте:\[R = \frac{\rho L}{A}\]

І таким чином, щоб отримати дійсно великий опір нам потрібен або дуже крихітний\(A\) (занадто важко досягти і контролювати), дійсно великий\(L\) (займає занадто багато місця на чіпі) або величезний\(\rho\) (знову ж таки, дуже важко контролювати, коли ви доберетеся до дуже низької щільності допінгу, яка буде потрібно).

Навіть якби ми могли знайти спосіб побудувати такі великі інтегральні схеми резисторів, все одно буде проблема. Струм, що протікає через резистор, коли MOSFET увімкнено, буде приблизно\[\begin{array}{l} I &= \frac{V}{R} \\ &= \frac{5 \mathrm{~V}}{10^{4} \ \Omega} \\ &= 5 \times 10^{-4} \mathrm{~A} \end{array}\]

Це не здається великим струмом, поки ви не вважаєте, що мікропроцесор Pentium © має близько 6 мільйонів воріт. Це означало б чистий струм,\(-300 \mathrm{~Amps}\) що протікає в чіп процесора! Ми повинні придумати краще рішення.