6.23: Проблеми
- Page ID
- 31743
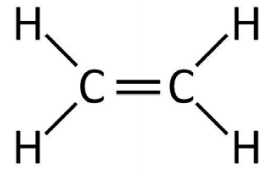
1. Розглянемо взаємодію двох атомів вуглецю кожен з одним електроном в прикордонній\(2p_{z}\) атомній орбіталі. Припускаючи, що положення атомів фіксовані, гамільтоніан системи складається з оператора кінетичної енергії та двох куломбічних потенційних членів: одного для центрального атома і одного для його сусіда:
\( H=T+V_{1}+V_{2} \)
Припустимо, що хвильова функція в цій системі двох атомів може бути записана як
\( \psi = c_{1}\phi_{1}+c_{2}\phi_{2} \)
де\(\phi_{1}\) і\(\phi_{2}\) є\(2p_{z}\) атомними орбіталями на першому і другому атомах вуглецю відповідно і і\(c_{1}\) і\(c_{2}\) є константами.
Власна енергія визначається як
\( \alpha_{r} = \left< \phi_{r}| T+V_{r} |\phi_{r} \right> \)
Перехідні взаємодії визначаються як
\( \beta_{sr} = \left< \phi_{s}| V_{s} |\phi_{r} \right> \)
Раніше ми припускали, що інтеграл перекриття між прикордонними орбіталями на атомних ділянках s і r може бути наближений як
\( S_{sr} = \left< \phi_{s}|\phi_{r} \right> = \delta_{sr} \)
Не варто робити тут такого припущення і показувати, що електронні енергії системи задовольняють.
\[ \det (H - ES) = 0 \nonumber \]
де H - гамільтонова матриця 2 × 2, а S - матриця перекриття 2 × 2, а E - константа.
(а) Запишіть кожну матрицю в Рівняння (6.24.1) з точки зору власних енергій, стрибкових інтегралів та інтегралів перекриття.
(б) За яких умов можна безпечно ігнорувати інтеграли перекриття?
2.
(а) Розглянемо потенціал\(V(x) = -V_{0}\delta(x)\), намальований нижче.
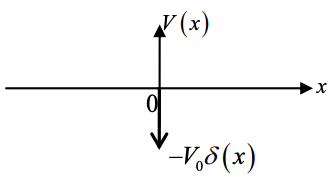
(i) Показати, що хвильова функція задається\(\phi_{1}(x) = \sqrt{k}e^{-k|x|}\) де\(k = \frac{mV_{0}}{\hbar^{2}}\)
(ii) Показати, що енергія зв'язаних станів (E<0) дорівнює\(E_{1} = -\frac{mV_{0}^{2}}{2\hbar^{2}}\).
(b) Тепер додайте другий потенціал дельта-функції при x = a.
тобто якщо попередній гамільтоніан був\(H_{1} = -\frac{\hbar^{2}}{2m} \frac{d^{2}}{dx^{2}}-V_{0}\delta(x)\), новий гамільтоніан - це\(H = H_{1}+V\) де\(V = -V_{0}\delta(x-a)\)
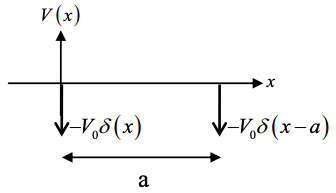
Нехай хвильова функція нової системи буде наближена\(\psi=c_{1}\phi_{1}+c_{2}\phi_{2}\) де\(\phi_{2} = \phi_{1}(x-a)\) і\(c_{1}\) і\(c_{2}\) є константами.
Самостійна енергія є\(\alpha = \left< \phi_{1}|H_{1}|\phi_{1} \right>\)
Взаємодія стрибків є\(\beta = \left< \phi_{2}|V|\phi_{1} \right>\)
Крім того, визначають інтеграл перекриття\(S = \left< \phi_{1}|\phi_{2} \right>\), і\(\gamma = \left< \phi_{1}|V|\phi_{1} \right>\)
Оцінюючи вирази
\( \left< \phi_{1} |H| \psi \right> = E \left< \phi_{1}|\psi \right> \)
і
\( \left< \phi_{2} |H| \psi \right> = E \left< \phi_{2}|\psi \right> \)
показати, що
\ (\ left (\ begin {масив} {cc}
\ альфа+\ гамма &\ альфа S+\ бета\
\ альфа S+\\ beta &\ alpha+
\ гамма\ кінець {масив}\ праворуч)\ left (\ begin {масив} {l}
c_ {1}\
c_ {2}
\ кінець {масив}\ праворуч) = E\ left (\ begin {масив} {c_}
1 & S \\
S & 1
\ end {масив}\ праворуч)\ лівий (\ begin {масив} {l}
c_ {1}\
c_ {2}
\ end {масив}\ справа)\)
Тепер покажіть, що\(\alpha = \frac{-mV_{0}^{2}}{2\hbar},\ \beta = \frac{-mV_{0}^{2}}{\hbar^{2}}e^{-ka},\ S(1+ka)e^{-ka}, \text{ and } \gamma=\frac{-mV_{0}^{2}}{\hbar^{2}}e^{-2ka}\)
Відкидаючи терміни\(e^{-2ka}\), що містять, показують, що матриця зводиться до\(E \approx \alpha \pm \beta\)
3. Для молекул, де кожен атом вуглецю вносить принаймні один делокалізований електрон до\(\pi\) орбіталі, ми можемо використовувати периметральну орбітальну теорію вільних електронів, яка описана нижче.
Припустимо, що розглянута молекула є круговим кільцем атомів і припускають нескінченний квадратний потенціал ями.
(а) Показати, що енергетичні рівні молекули при цьому наближенні є
\( E = \frac{h^{2}m_{l}^{2}}{2m_{e}L^{2}} \)
де де\(m_{l}\) - ціле число, а L - периметр молекули.
Підказка: Гамільтоніан у полярних координатах задається:
\( \hat{H} = \frac{\hbar^{2}}{2m_{e}}\left( \frac{d^{2}}{dr^{2}}+\frac{1}{r}\frac{d}{dr}+\frac{1}{r^{2}}\frac{d^{2}}{d\phi^{2}} \right) \)
(b) Відповідно до наближення теорії орбіти вільних електронів периметра, структура енергетичного рівня антрацену показана на малюнку 6.24.3 нижче.
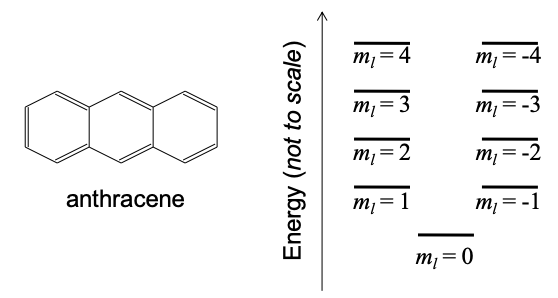
(i) Чому існує рішення для\(m_{l} = 0\) в антрацені, але немає рішення для n = 0 в нескінченній квантовій ямі?
(ii) Чому\(m_{l}\) в антрацені існують розв'язки для негативу, але немає розв'язків для негативних n в нескінченній квантовій ямі? Підказка: розглянемо принцип виключення Паулі.
(c) Обчисліть молекулярні орбіталі та проміжок HOMO-LUMO антрацену. Візьміть a = 1.38Å як довжину зв'язку C-C. Припустимо, що кожен атом С дарує 1 електрон прикордонним орбіталям.
4. Розглянемо періодичну молекулу, що складається з двох різних змінних типів атомів, проілюстрованих нижче (наведені прикордонні орбіталі).

(а) Скільки атомів знаходиться в одиничній клітині цієї молекули? Використовуючи періодичні граничні умови і припускаючи молекулярні хвильові функції форми Блоха, знайдіть енергетичні рівні.
(б) Знайти щільність станів.
5. Смугова структура молекулярних кристалів
\(\phi({\bf{r}})\)Дозволяти бути HOMO типової молекули. Як і в більшості стабільних молекул,\(\phi({\bf{r}})\) повністю зайнятий і містить два електрони.
На відміну від звичайних кристалічних напівпровідників, таких як Si, одиничні клітини в молекулярному кристалі утримуються разом слабкими силами ван дер Ваальса. Типовим значенням взаємодії найближчих сусідів у твердому тілі, пов'язаному ван дер Ваальсом, є
\( \beta=\left< \phi({\bf{r+R}})|H| \phi({\bf{r}})\right> \approx -10\ meV \)
де H - гамільтоніан для взаємодії між найближчими сусідами, а R - сукупність векторів решітки, що з'єднують молекулу при r з найближчими сусідами.
(а) Обчисліть структуру «валентної» зони кубічного молекулярного кристала цієї молекули. Нехай\(\left<\phi({\bf{r}})|H| \phi({\bf{r}})\right> = \alpha\). (Див. Рис. 6.24.5 нижче).
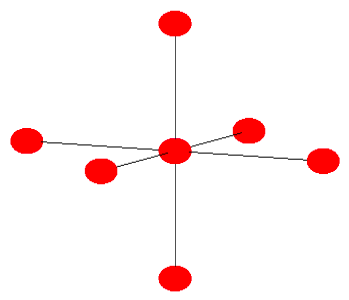
(б) Показати, що всі молекулярні кристали із заповненими ГОМО є ізоляторами.
6. Розглянемо наступний полімер:

Припустимо, відстань між атомами на лінійній магістралі є\(a_{0}\), як показано на малюнку. Крім того, припустимо, що всі атоми є одним елементом,\(\beta_{1}\) і\(\beta_{2}\) є стрибковими взаємодіями між атомами, як показано, власна енергія кожного атома є\(\alpha\), і припускаємо, що кожен атом вносить один електрон.
(а) Що таке примітивна одинична клітина і примітивний гратчастий вектор?
(b) Показати, що співвідношення дисперсії задається
\( E = \alpha +\beta_{2}\ cos(ka_{0}) \pm \sqrt{\beta_{2}^{2}\ cos^{2}(ka_{0})+2\beta_{1}^{2}(1+cos(ka_{0}))} \)
(c) Полімер металевий або ізоляційний?
7. Транзистори графенові та вуглецеві нанотрубки
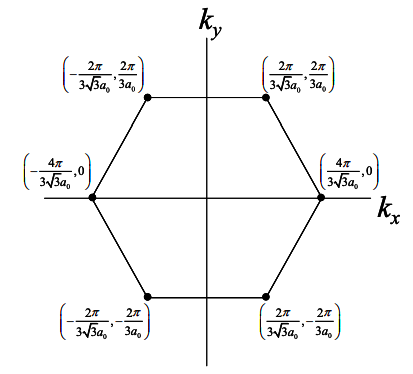
(а) З посиланням на смугову структуру графена, показану нижче, поясніть, чому графен при згортанні в нанотрубки може бути або металевим, або напівпровідниковим?
(b) Використовуючи графік k -простору, показаний нижче, визначити, чи є наступні (n, m) нанотрубки металевими або напівпровідниковими. Нагадаємо, що нанотрубки - це згорнуті графенові листи з обгортковим вектором\(\bar{w}=na_{1}+ ma_{2}=(n,m)\).
i) (0,6)
ii) (Н, Н)
іii) (3,9)
iv) (3,5)
(c) В даний час існує великий інтерес до використання графена (на відміну від вуглецевих нанотрубок) як канального матеріалу для польових транзисторів. Ідея полягає в тому, щоб виготовити цілі чіпи на одному аркуші графена.
Спочатку графен депонується якимось чином (в даний час це технологічний виклик). Далі графен вирізається. Нарешті, контакти і ізолятори затвора осідають.
Чому графен вирізається? Поясніть з посиланням на частинки в коробці моделі провідників.
8. Вуглецеві нанотрубки
(а) Доведіть тотожності в рівнянні (6.21.3) та рівнянні (6.21.4).
(b) Вивести рівняння (6.21.6) з рівняння (6.21.5).
9. Це питання стосується молекули, показаної нижче.
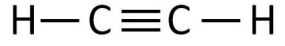
а) Запишіть гамільтонову матрицю для цієї молекули з точки зору параметрів щільного зв'язування\(\alpha\), і\(\beta\).
б) Запишіть енергію для цієї молекулярної орбіти з точки зору\(\alpha\) і\(\beta\).
в) Порівняйте щільність станів HOMO і LUMO попередньої молекули з наведеною нижче.