Skip to main content
LibreTexts - Ukrayinska

6.3: Молекулярні орбіталі

  1. Last updated
  2. Save as PDF
  • Page ID
    31755

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    На жаль, навіть коли ми застосовуємо наближення Борна-Оппенгеймера і тримаємо ядерні координати фіксованими, рішення рівняння Шредінгера (Equation (6.2.5)) є надзвичайно складним у всіх, крім найпростіших молекул. Зазвичай віддають перевагу числовим методам. Але деяке концептуальне розуміння можна отримати, припускаючи, що молекулярні орбіталі є лінійними комбінаціями атомних орбіталів, тобто ми пишемо:

    \[ \varphi = \sum_{r} c_{r}\phi_{r} \nonumber \]

    де\(\varphi\) молекулярна орбіталь і\(\phi\) атомна орбіталь. Заповнена молекулярна орбіталь з меншою енергією, ніж складові атомні орбіталі, стабілізує молекулу і відома як хімічний зв'язок.

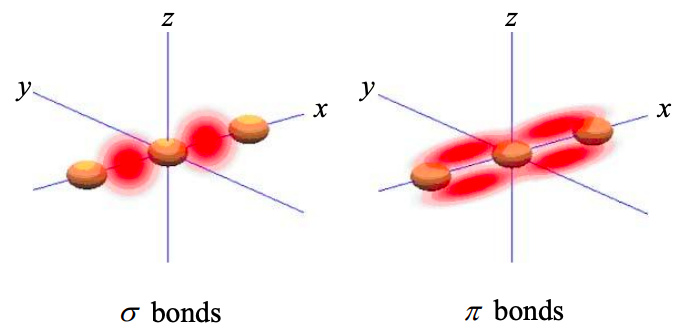
    Ми можемо визначити два типи молекулярних орбіталів, побудованих з атомних орбіталів s та p:

    \(\sigma\)молекулярні орбіталі: Вони локалізуються між атомами і є інваріантними щодо обертань навколо міжядерної осі. Якщо ми можемо взяти вісь x як міжядерну вісь, то в\(sigma\) молекулярних орбіталах можуть брати участь як s, так і\(p_{x}\) атомні орбіталі. \(p_{y}\)і\(p_{z}\) атомні орбіталі не можуть сприяти s молекулярних орбіталів, оскільки кожен з них має нульову щільність ймовірності на осі x.

    \(\pi\)молекулярні орбіталі: Електрони на\(\pi\) молекулярних орбіталах легше поділяються між атомами. Щільність ймовірності не така локалізована, як в\(\sigma\) молекулярній орбіталі. \(\pi\)Молекулярна орбіталь також не інваріантна щодо обертань навколо міжядерної осі. лінійні комбінації\(p_{y}\) і\(p_{z}\) атомні орбіталі утворюють\(\pi\) молекулярні орбіталі.

    Знімок екрана 2021-05-24 о 17.01.42
    Малюнок\(\PageIndex{1}\): Приклади\(\sigma\) і\(\pi\) облігацій. \(\sigma\)зв'язки локалізуються між атомами, тоді як\(\pi\) зв'язки делокалізовані над міжядерною віссю.