Skip to main content
LibreTexts - Ukrayinska

6.1: Атом водню

  1. Last updated
  2. Save as PDF
  • Page ID
    31775

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Водень - найпростіший елемент. Всього дві складові: електрон і позитивно заряджене ядро, що складається з одного протона.

    Електрон відчуває привабливий потенціал ядра. Ядерний потенціал сферично симетричний і задається кулонівським потенціалом

    \[ V(r) = -\frac{Zq^{2}}{4\pi \epsilon_{0}r} \nonumber \]

    де r - радіальне поділ електрона, а ядро\(\epsilon_{0}\) - діелектрична проникність, а Z - число позитивних зарядів у ядра. Для водню є один протон, а Z = 1.

    Нагадаємо, що загальним виразом для оператора кінетичної енергії в трьох вимірах є:

    \[ \hat{T} = - \frac{\hbar^{2}}{2m_{e}}\nabla^{2} \nonumber \]

    де\(\nabla^{2}\) - оператор Лапласа.

    У прямолінійних координатах (x, y, z)

    \[ \nabla^{2} = \frac{d^{2}}{dx^{2}}+\frac{d^{2}}{dy^{2}}+\frac{d^{2}}{dz^{2}} \nonumber \]

    У сферичних координатах\((r, \theta, \phi)\)

    \[ \nabla^{2} = \frac{1}{r}\frac{d^{2}}{dr^{2}}+\frac{1}{r^{2}}\frac{1}{sin^{2}\theta}\frac{d^{2}}{d\phi^{2}}+\frac{1}{r^{2}}\frac{1}{sin\theta}\frac{d}{d\theta}sin\theta \frac{d}{d\theta} \nonumber \]

    Таким чином, гамільтоніан для атома водню

    \[ \hat{H} = -\frac{\hbar^{2}}{2m} \nabla^{2} - \frac{Zq^{2}}{4\pi\epsilon_{0}r} \nonumber \]

    \( = -\frac{\hbar^{2}}{2m} \left( \frac{1}{r}\frac{d^{2}}{dr^{2}}r +\frac{1}{r^{2}}\frac{1}{sin^{2}\theta}\frac{d^{2}}{d\phi^{2}}+\frac{1}{r^{2}}\frac{1}{sin \theta}\frac{d}{d\theta}sin\theta \frac{d}{d\theta} \right) - \frac{Zq^{2}}{4\pi\epsilon_{0}r} \)

    Це вимагає трохи алгебри для вирішення атомних орбіталів і пов'язаних з ними енергій. Приблизне рішення (припускаючи, що потенціал коробки, а не правильний кулонівський потенціал) міститься в Додатку 2.

    Найнижчі енергетичні рішення побудовані на малюнку 6.2.1, нижче

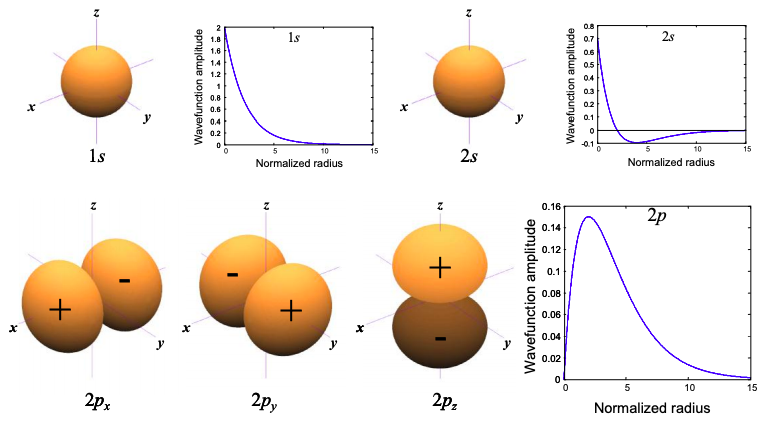
    Скріншот 2021-05-24 о 16.44.40 png
    Малюнок\(\PageIndex{1}\): Перші п'ять орбіталей атома водню разом з їх радіальними профілями.

    Кожен з розчинів, показаних на малюнку 6.2.1, маркується або s, або p. Ці букви описують кутову симетрію рішення. Вони є індексом для орбітального моменту моменту електрона. Орбіталі «s» демонструють навіть симетрію щодо походження в кожному вимірі. Орбіталі, які демонструють непарну симетрію щодо походження в одному вимірі, маркуються «p». У Додатку 1 показано, що власні функції електрона, обмеженого поверхнею сфери, характеризуються квантованим кутовим імпульсом. Ми показуємо лише s та p розв'язки, але існує нескінченний набір рішень, наприклад s, p, d, f..., що відповідають орбітальним кутовим моментам 0, 1, 2, 3...

    Енергія кожної атомної орбіти також позначена цілим числом, відомим як головне квантове число. Таким чином, 1-я орбіталь - це найнижча енергія s орбіталі, 2p і 2s орбіталі є виродженими першими збудженими станами.

    Знання точних атомних орбіталів не є необхідним для наших цілей. Швидше, ми будемо використовувати орбіталі як символічні будівельні блоки при побудові молекулярних орбіталів: хвильові функції електронів у молекулах.