Skip to main content
LibreTexts - Ukrayinska

2.3: Поточний

  1. Last updated
  2. Save as PDF
  • Page ID
    31867

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розподіл електронів всередині матеріалу визначає його провідність. Як приклад розглянемо деякі рухомі електрони в гаусовому хвильовому пакеті. Хвильовий пакет у свою чергу може бути описаний зваженою суперпозицією плоских хвиль. Тепер ми знаємо з попереднього розділу, що, якщо хвильовий пакет не зосереджений на k = 0 в k -просторі, то він буде рухатися і струм буде текти.

    Є й інший спосіб подивитися на це. Зверніть увагу, що існують компоненти плоских хвиль з\(+k_{z}\) обома і\(-k_{z}\) хвильовими числами. Таким чином, навіть коли електрон нерухомий, компоненти хвильового пакета рухаються в обох напрямках. Але якщо кожен компонент, що рухається в\(+k_{z}\) напрямку, врівноважується компонентом, що рухається в\(-k_{z}\) напрямку, немає чистого струму.

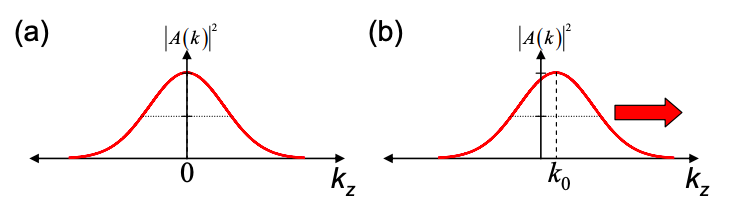
    Знімок екрана 2021-04-15 о 21.08.12.png
    Малюнок\(\PageIndex{1}\): Хвильовий пакет без чистої швидкості. Відзначимо, що кожна плоска\(+k_{z}\) хвильова складова з хвильовимчислом компенсується\(-k_{z}\) плоскою хвильовою складовою з хвильовим числом. (b) Хвильовий пакет з чистою швидкістю в позитивному напрямку z асиметричний про\(k_{z} = 0\).

    У цьому розділі ми покажемо, що ми можемо застосувати подібний аналіз до електронів всередині провідника. Наприклад, електрони в дроті займають стани з різними хвильовими числами, відомими як k -стани. Кожне з цих станів може бути змодельовано плоскою хвилею і існують стани, які поширюються в обох напрямках.

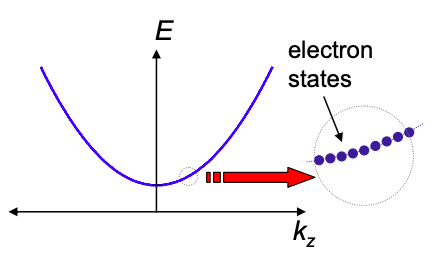
    Нагадаємо, що для плоської хвилі

    \[ E = \frac{\hbar^{2}k_{z}^{2}}{2m} \nonumber \]

    Це співвідношення між енергією і хвильовимчислом відомо як дисперсійне відношення. Для плоских хвиль це параболічна крива. Нижче кривої відсутні електронні стани. Таким чином, електрони перебувають в межах певної смуги енергій. \(^{†}\)

    Скріншот 2021-04-15 о 21.11.38.png
    Малюнок\(\PageIndex{2}\): Електрони в дроті займають стани з різними енергіями і хвильовими числами.

    В умовах рівноваги дріт заповнюється електронами аж до енергії Фермі,\(E_{F}\). Електрони заповнюють обидва\(+k_{z}\) і\(-k_{z}\) стани, і поширюються однаково в обох напрямках. Струм не протікає. Ми говоримо, що ці електрони компенсуються.

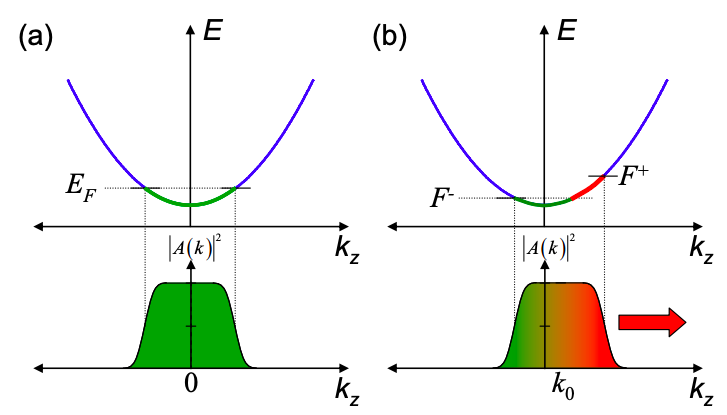
    Знімок екрана 2021-04-15 о 21.12.58.png
    Малюнок\(\PageIndex{3}\): (а) В умовах рівноваги електрони спочатку заповнюють найнижчу енергію k -станів. Оскільки заповнені рівні числа\(+k_{z}\) і\(-k_{z}\) станів, чистий струм відсутній. (b) Коли\(+k_{z}\) і\(-k_{z}\) стани заповнені на різних рівнях, існує чистий струм.

    Щоб чистий струм протікав, повинна бути різниця в кількості електронів, що рухаються в кожному напрямку. Таким чином, електрони, що рухаються в одному напрямку, не можуть перебувати в рівновазі з електронами, що рухаються в іншому. Ми визначаємо два квазі-рівні Фермі:\(F^{+}\) це енергетичний рівень, коли стани з наполовину\(k_{z}>0\) заповнені,\(F^{-}\) є відповідним енергетичним рівнем для станів с\(k_{z}<0\). Ми бачимо, що потік струму пов'язаний з різницею в рівнях квазі Фермі та наявністю електронних станів між рівнями квазі Фермі. Якщо між\(F^{+}\) і немає електронів\(F^{-}\), то матеріал є ізолятором і не може проводити заряд.

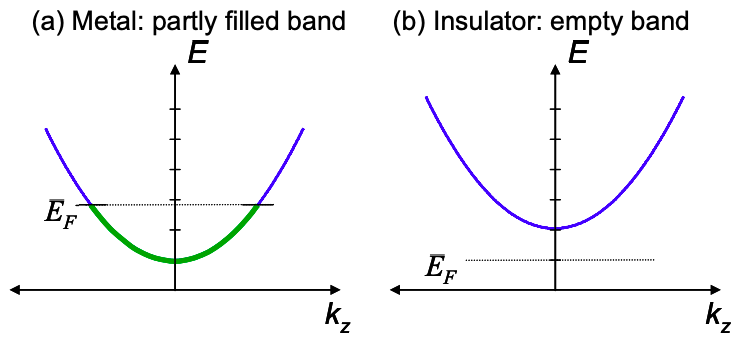
    Скріншот 2021-04-15 о 21.15.55.png
    Малюнок\(\PageIndex{4}\): Приклади металу (а) і ізолятора (б).

    Підсумовуємо: струм переноситься некомпенсованими електронами.

    \(^{†}\)Строго смуга потребує верхньої, а також нижньої межі дозволеної енергії, тоді як проста модель плоских хвиль дає лише нижню межу. Пізніше ми також знайдемо верхні межі в більш точних моделям матеріалів. Зауважте також, що 0-d матеріали, такі як молекули або квантові точки, не мають смуг, оскільки електрони обмежені у всіх напрямках і не можуть бути змодельовані плоскою хвилею в будь-якому напрямку.