Skip to main content
LibreTexts - Ukrayinska

2.15: Проблеми

  1. Last updated
  2. Save as PDF
  • Page ID
    31827

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    1.

    i) Використовуючи MATLAB, згенеруйте малюнок 2.7.2

    ii) Якщо\(L_{y} = L_{x} \cdot \sqrt{\frac{3}{5}}\) який режим має меншу енергію {\(n_{x}= 3,n_{y} = 1\)} або {\(n_{x}= 2, n_{y} = 2\)}

    2. Транзистор, показаний нижче, має товщину оксиду (\(\epsilon = 4\epsilon_{0}\)) d = 1,2 нм і глибину каналу\(L_{z}\) = 2,5 нм. Розглядаючи канал як квантову яму, скільки режимів заповнюється при подачі напруги V = 1V на затвор?

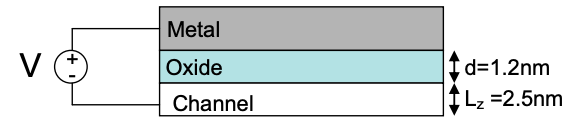
    Знімок екрана 2021-04-20 о 21.19.55, png
    Малюнок\(\PageIndex{28}\): Проста модель сучасного транзистора.

    Підказка: обчислити заряд в каналі за допомогою виразу для паралельного пластинчастого конденсатора.

    3. Конкретний провідник довжиною L має дисперсійне відношення:

    \ [\ begin {масив} {l}
    E_ {1} (k) =5+2 V\ cos (k a)\\
    E_ {2} (k) =10-2 V\ cos (k a)
    \ end {масив}, |k|<\ frac {\ pi} {a}\ nonumber\]

    де V і a - позитивні константи.

    i) Намалюйте співвідношення дисперсії.

    ii) Обчислити щільність станів в перерахунку на E, V і a.

    4. В цілому вироджене наближення для функції розподілу електронів\(f(E,E_{F})\) працює, коли щільність станів велика і повільно змінюється вище і нижче рівня Фермі. Невироджене наближення найкраще працює тоді, коли щільність станів на рівні Фермі значно менша, ніж щільність станів при вищих енергіях.

    Тут розглядаються ці наближення в гаусовій густини станів. Гауссова досить повільно змінюється біля свого центру, але вкрай швидко зменшується в хвостах. Популяція електронів у гауссовій густини станів задається

    \[ n = \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi\sigma^{2}}} e^{-\frac{1}{2}(E/\sigma)^{2}}f(E,E_{F})dE \nonumber \],

    \(f(E,E_{F})\)де функція Фермі. Для певного діапазону рівня Фермі\(E_{F}\) популяція електронів може бути наближена як:

    \[ n \approx \int^{E_{F}}_{-\infty} \frac{1}{\sqrt{2\pi\sigma^{2}}} e^{-\frac{1}{2}(E/\sigma)^{2}}dE \nonumber \]

    Це вироджена межа.

    При зниженні рівня Фермі популяцію електронів краще розраховувати в невиродженій межі. Вивести мінімальний рівень Фермі\(E_{F}\) для виродженої межі в залежності від температури T і стандартного відхилення\(\sigma\).

    Підказка: оцініть мінімальний рівень Фермі, вивчивши енергетичний розподіл електронів у невиродженій межі.