Skip to main content
LibreTexts - Ukrayinska

1.20: Застосування принципу невизначеності

  1. Last updated
  2. Save as PDF
  • Page ID
    31936

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Принцип невизначеності зазвичай не є значним у повсякденному житті. Наприклад, якщо невизначеність в імпульсі 200g більярдного кулі, що рухається зі швидкістю 1 м/с, становить 1%, ми можемо в принципі знати його положення\(\Delta x = (\hbar/2)/(0.2/100) = 3 \times 10^{-32} m\).

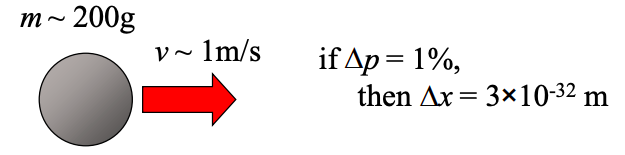
    Знімок екрана 2021-04-15 о 10.00.53.png
    Малюнок\(\PageIndex{18}\): Принцип невизначеності не дуже актуальний для побутових предметів

    Однак у наноелектроніці принцип невизначеності може зіграти певну роль.

    Для прикладу розглянемо дуже тонкий провід, через який по одному проходять електрони. Струм в дроті пов'язаний з часом проходження кожного електрона

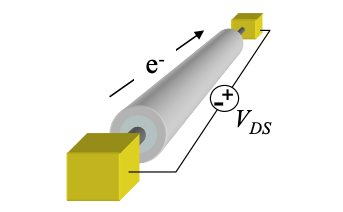
    Знімок екрана 2021-04-15 о 10.01.48.png
    Малюнок\(\PageIndex{19}\): Нанодріт, який пропускає один електрон за раз

    \[ I =\frac{q}{\tau} \nonumber \]

    де q - заряд одного електрона.

    Для отримання струму I = 0,1 мА в дроті час проходження кожного електрона має бути

    \[ \tau = \frac{q}{I} \approx 1.6fs \nonumber \]

    Час транзиту - це час, який електрон існує всередині дроту. Деякі електрони можуть подорожувати через дріт швидше, а деякі повільніше, але ми можемо наблизити невизначеність у житті електрона\(\Delta t = \tau = 1.6fs\). \(^{†}\)

    З Рівняння (1.19.1) ми знаходимо це\(\Delta E = 0.2\ eV\). Таким чином, невизначеність в енергії електрона еквівалентна випадковому потенціалу приблизно\(0.2 V.^{\S}\) Як ми побачимо, такі ефекти принципово обмежують комутаційні характеристики нанотранзисторів.

    \(^{†}\)Ще один спосіб подумати про це - розглянути додавання електрона до нанодроту. Якщо струм повинен текти, цей електрон повинен мати можливість рухатися від дроту до контакту. Швидкість, з якою він може це зробити (тобто його термін служби на дроті) обмежує час проходження електрона і, отже, струм, який може протікати в дроті.

    \(^{\S}\)Нагадаємо, що сучасні транзистори працюють при напрузі ~ 1В. Таким чином, ця невизначеність є суттєвою.