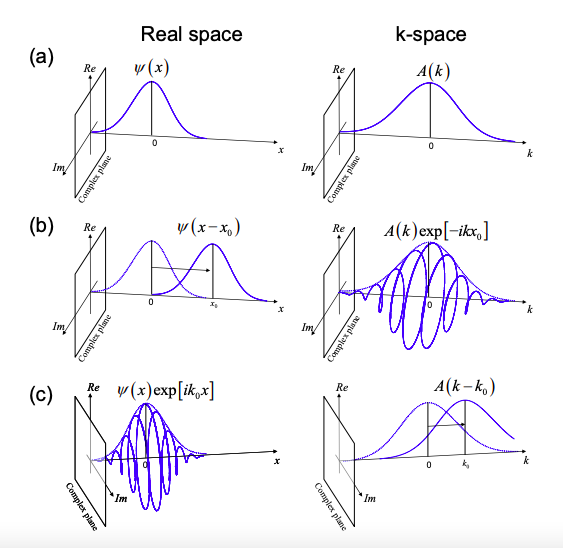
1.11: Приклади хвильових пакетів
- Page ID
- 31898
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Типовий гауссовий хвильовий пакет показаний на малюнку 1.11.1 як у реальному просторі, так і у k-просторі. Спочатку розподіл ймовірностей зосереджений на x = 0 і k = 0. Якщо зсунути хвильовий пакет у k-просторі до середнього значення\(\langle k\rangle = k_{0}\), це еквівалентно множенню на фазовий коефіцієнт\(\text{ exp}[ik_{0}x]\) у реальному просторі. Аналогічно, зсув центру хвильового пакету в реальному просторі до\(\langle x\rangle = x_{0}\) еквівалентно множенню k -простору подання на фазовий коефіцієнт\(\text{ exp}[ikx_{0}]\).
| Реальні координати (x, t) | \(\rightleftharpoons\) | Зворотні координати (k,\(\omega\)) |
|---|---|---|
| зрушення на\(x_{0}\) | \ (\ правий лівий гарпуни\) ">\(\rightleftharpoons\) | \ (\ омега\) ">\(\times \text{ exp}[-ikx_{0}]\) |
| \(\times \text{ exp}[ik_{0}x]\) | \ (\ правий лівий гарпуни\) ">\(\rightleftharpoons\) | \ (\ омега\) ">зрушення на\(k_{0}\) |
| зрушення на\(t_{0}\) | \ (\ правий лівий гарпуни\) ">\(\rightleftharpoons\) | \ (\ омега\) ">\(\times \text{ exp}[i\omega t_{0}]\) |
| \(\times \text{ exp}[-i\omega_{0}t]\) | \ (\ правий лівий гарпуни\) ">\(\rightleftharpoons\) | \ (\ омега\) ">зрушення на\(\omega_{0}\) |