Skip to main content
LibreTexts - Ukrayinska

6.9: Моделі каналів

  1. Last updated
  2. Save as PDF
  • Page ID
    33154

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Як провідні, так і бездротові канали поділяють характеристики, що дозволяє нам використовувати загальну модель того, як канал впливає на передані сигнали.

    Як провідні, так і бездротові канали поділяють характеристики, що дозволяє нам використовувати загальну модель того, як канал впливає на передані сигнали.

    • Переданий сигнал зазвичай не фільтрується каналом.
    • Сигнал можна послабити.
    • Сигнал поширюється по каналу зі швидкістю, рівною або меншою швидкості світла, а значить, канал затримує передачу.
    • Канал може вводити адитивні перешкоди і/або шум.

    Дозволяючи α представляти загасання, введене каналом, вхідний сигнал приймача пов'язаний з переданим

    \[r(t)=\alpha x(t-\tau )+i(t)+n(t) \nonumber \]

    Цей вираз відповідає моделі системи для каналу, показаної на малюнку 6.9.1 нижче. У цій книзі ми будемо вважати, що шум білий.

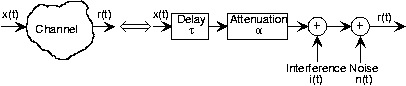
    Малюнок 6.9.1 Канальна складова фундаментальної моделі зв'язку має зображений вигляд. Затухання відбувається через втрати поширення. Додавання перешкод і шумів обґрунтовано властивістю лінійності рівнянь Максвелла.
    Вправа\(\PageIndex{1}\)

    Чи є ця модель для каналу лінійної?

    Рішення

    Канал адитивного шуму не є лінійним, оскільки він не має властивості нульового вводу-нульового виходу (хоча ми можемо нічого не передавати, вхід приймача складається з шуму).

    Як і очікувалося, сигнал, який виходить з каналу, пошкоджений, але дійсно містить переданий сигнал. Проектування системи зв'язку починається з деталізації моделі каналу, а потім розробки передавача і приймача, які найкраще компенсують корупційну поведінку каналу. Охарактеризуємо якість каналу співвідношенням сигнал/перешкода (SIR) і відношенням сигнал/шум (SNR). Коефіцієнти обчислюються відповідно до відносної потужності кожного в межах пропускної здатності переданого сигналу. Припускаючи, що спектр сигналу x (t) охоплює частотний інтервал [f l, f u], ці співвідношення можуть бути виражені через спектри потужності.

    \[SIR=\frac{2\alpha ^{2}\int_{0}^{\infty }P_{x}(f)df}{2\int_{f_{l}}^{f_{u}}P_{i}(f)df} \nonumber \]

    \[SNR=\frac{2\alpha ^{2}\int_{0}^{\infty }P_{x}(f)df}{N_{0}(f_{u}-f_{l})} \nonumber \]

    У більшості випадків потужність перешкод і шуму не змінюються для даного приймача. Варіації співвідношення сигнал-перешкода та сигнал-шум виникають внаслідок загасання через зміни відстані передавача до приймача.