5.15: Ефективність частотно-доменної фільтрації
- Page ID
- 32924
- Порівнює ефективність фільтрації частотної області та часової області.
Щоб визначити, для яких тривалості сигналу та фільтрів реалізація часової або частотної області була б найбільш ефективною, нам потрібно лише підрахувати обчислення, необхідні кожному. Для підходу в часовій області, різницево-рівняння нам потрібно
\[(N_{X}+q)(2(q)+1) \nonumber \]
Частотно-доменний підхід вимагає трьох перетворень Фур'є, кожна з яких вимагає
\[\frac{5K}{2}(\log_{2}K) \nonumber \]
обчислення для довжини K БПФ, і множення двох спектрів (6K обчислень). Довжина вихідного сигналу, визначена тривалістю, повинна бути не менше
\[N_{x}+q \nonumber \]
Таким чином, ми повинні порівняти
\[(N_{x}+q)(2q+1)\leftrightarrow 6(N_{x}+q)+5(N_{x}+q)\log _{2}(N_{x}+q) \nonumber \]
Точна аналітична оцінка цього порівняння досить складна (нам належить розв'язати трансцендентне рівняння). Пониження з цим порівнянням найкраще отримати шляхом ділення на N x + q.
\[2q+1\leftrightarrow 6+5\log _{2}(N_{x}+q) \nonumber \]
За допомогою цієї маніпуляції ми оцінюємо кількість обчислень на зразок. Для будь-якого заданого значення порядку фільтра q права сторона, кількість обчислень частотної області, перевищить ліву, якщо тривалість сигналу досить довга. Однак, для тривалості фільтра, що перевищує приблизно 10, якщо вхід становить принаймні 10 зразків, підхід частотної області є швидшим до тих пір, поки обмеження потужності двох БПФ є вигідним.
Частотно-доменний підхід ще не життєздатний; що ми будемо робити, коли вхідний сигнал нескінченно довгий? Сценарій різницевого рівняння ідеально відповідає передбаченій структурі цифрової фільтрації, але поки що ми вимагали, щоб вхід мав обмежену тривалість (щоб ми могли обчислити його перетворення Фур'є). Рішення цієї проблеми досить просте: розділіть вхід на кадри, відфільтруйте кожен і додайте результати разом. Розділити сигнал означає вираження його у вигляді лінійної комбінації довжини- N х неперекриваються «шматків». Оскільки фільтр лінійний, фільтрація суми термінів еквівалентна підсумовуванню результатів фільтрації кожного члена.
\[\left ( x(n)=\sum_{m=-\infty }^{\infty }x(n-mN_{x}) \right )\Rightarrow \left ( y(n)=\sum_{m=-\infty }^{\infty }y(n-mN_{x}) \right ) \nonumber \]
Як показано на малюнку 5.15.1 нижче, зверніть увагу, що кожен відфільтрований розділ має тривалість більше, ніж вхідні дані. Отже, ми повинні буквально додавати фільтровані розділи разом, а не просто стикувати їх разом.
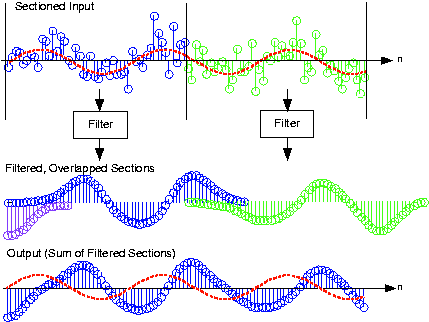
Обчислювальні міркування виявляють істотну перевагу для реалізації частотної області над часовою областю. Кількість обчислень для реалізації часової області по суті залишається постійною, незалежно від того, розділяємо ми вхідні дані чи ні. Таким чином, кількість обчислень для кожного виходу дорівнює 2 (q) +1. У підході до частотної області підрахунок обчислень змінюється, оскільки нам потрібно лише один раз обчислити частотну характеристику фільтра H (k), що становить фіксовані накладні витрати. Нам потрібно лише обчислити два DFT і помножити їх, щоб відфільтрувати розділ. Дозволивши N x позначити довжину секції, кількість обчислень для розділу дорівнює:
\[(N_{x}+q)\log _{2}(N_{x}+q)+6(N_{x}+q) \nonumber \]
Крім того, ми повинні додати відфільтровані виходи разом; кількість членів, які потрібно додати, відповідає надлишковій тривалості виходу порівняно з входом (q). Таким чином, підхід до частотної області вимагає:
\[\log _{2}(N_{x}+q)+6+\frac{q}{N_{x}+q} \nonumber \]
обчислень на вихідне значення. Для навіть скромних замовлень фільтрів підхід частотно-доменний набагато швидше.
Покажіть, що зі збільшенням довжини перерізу підхід до частотної області стає все більш ефективним.
Рішення
Нехай N позначає загальну тривалість вхідних даних. Реалізація часової області вимагає загальної кількості N (2q+1) обчислень, або 2 (q) +1 обчислень на вхідне значення. У частотній області ми розбиваємо вхід на N/ N x секції, кожен з яких вимагає
\[\log _{2}(N_{x}+q)+6+\frac{q}{N_{x}+q} \nonumber \]
за вхід в секції. Оскільки ми знову ділимо на N х, щоб знайти кількість обчислень на вхідне значення у всьому вхідному значенні, ця величина зменшується, коли N x збільшується. Для реалізації часової області вона залишається постійною.
Зверніть увагу, що вибір тривалості розділу довільний. Після того, як фільтр обраний, ми повинні розділити так, щоб необхідна довжина БПФ була точно потужністю два: Виберіть N x, щоб
\[N_{x}+q=2^{L} \nonumber \]
Реалізація цифрового фільтра, показаного на блок-схемі A/D з реалізацією частотної області, вимагає деякого додаткового управління сигналами, не вимагається реалізаціями часової області. Концептуально фільтр часової області в режимі реального часу може приймати кожен зразок, коли він стає доступним, обчислити різницеве рівняння та виробляти вихідне значення, все менше, ніж інтервал вибірки T S. Підходи до частотної області не працюють на основі вибірки за зразком; натомість вони працюють на розділах. Вони фільтрують в режимі реального часу, виробляючи N x виходів для такої ж кількості входів швидше, ніж N x T S. Оскільки вони, як правило, займають більше часу, щоб створити вихідний розділ, ніж тривалість інтервалу вибірки, ми повинні фільтрувати один розділ, приймаючи в пам'ять наступний розділ для фільтрації. У програмуванні операція створення розділів під час обчислень на попередніх відома як буферизація. Буферизація також може бути використана в фільтрах часової області, але це не обов'язково.
Ми хочемо, щоб нижні частоти фільтрували сигнал, який містить синусоїду і значну кількість шуму. Приклад, показаний на малюнку, показує частину форми сигналу галасливого сигналу. Якби не накладена синусоїда, розрізнити синусоїду в сигналі практично неможливо. Одним з основних застосувань лінійних фільтрів є видалення шуму: зберегти сигнал шляхом узгодження смуги пропускання фільтра зі спектром сигналу і значно зменшити всі інші частотні компоненти, які можуть бути присутніми в галасливому сигналі.
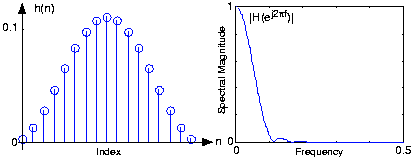
Розумний інженер Райс вибрав фільтр FIR, який має реакцію одиничного зразка, що відповідає синусоїді періоду 17:
\[h(n)=\frac{1}{17}\left ( 1-\cos \left ( \frac{2\pi n}{17} \right ) \right ),n=\left \{ 0,...,16 \right \}\; which\; makes\; q=16 \nonumber \]
Його частотна характеристика (визначається обчисленням дискретного перетворення Фур'є) показана на малюнку 5.15.2 нижче. Щоб застосувати, ми можемо вибрати довжину кожного розділу так, щоб підхід до фільтрації частотної області був максимально ефективним: Виберіть довжину секції N x так, щоб N x + q був потужність двох. Щоб використовувати довжину-64 БПФ, кожна секція повинна мати довжину 48 зразків. Фільтрація з різницевим рівнянням вимагатиме 33 обчислень на вихід, тоді як частотна область вимагає трохи більше 16; ця реалізація частотної області перевищує вдвічі швидше! На малюнку 5.15.1 показано, як працює фільтрація частотної області.
Відзначимо, що шум був різко зменшений, при цьому синусоїда тепер добре видно на відфільтрованому виході. Деякі залишкові шуми залишаються через те, що компоненти шуму в смузі пропускання фільтра з'являються на виході, а також сигнал.
Зверніть увагу, що порівняно з синусоїдальною складовою вхідного сигналу, синусоїдальна складова виходу, здається, затримується. Що є джерелом цієї затримки? Чи можна його видалити?
Рішення
Затримка тут не є затримкою обчислень - графік показує, що перше вихідне значення вирівнюється з першим входом фільтра - хоча в реальних системах це є важливим фактором. Швидше за все, затримка обумовлена фазовим зсувом фільтра: Зсунута по фазі синусоїда еквівалентна затримці за часом:
\[\cos \left ( 2\pi fn-\varphi \right )=\cos \left ( 2\pi f\left ( n-\frac{\varphi }{2\pi f} \right ) \right ) \nonumber \]
Всі фільтри мають фазові зсуви. Ця затримка може бути видалена, якщо фільтр не ввів фазового зсуву. Такі фільтри не існують в аналоговому вигляді, але цифрові можна запрограмувати, але не в реальному часі. Це вимагатиме виходу, щоб з'явитися до того, як надійде вхід!
