3.14: Проектування функцій передачі

Last updated
Save as PDF

Page ID: 33129

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Цей модуль узагальнює ключові поняття передавальних функцій та містить приклади використання передавальних функцій.

Якщо джерело складається з двох (або більше) сигналів, ми знаємо з теорії лінійної системи, що вихідна напруга дорівнює сумі виходів, вироблених кожним сигналом окремо. Коротше кажучи, лінійні схеми - це особливий випадок лінійних систем, і тому застосовується суперпозиція. Зокрема, припустимо, що ці складові сигнали є складними експоненціальними, кожна з яких має частоту, відмінну від інших. Функція передачі зображує, як схема впливає на амплітуду і фазу кожного компонента, дозволяючи зрозуміти, як схема працює на складному сигналі. Ці компоненти, що мають частоту менше частоти зрізу, проходять через схему з невеликою модифікацією, тоді як ті, що мають більш високі частоти, пригнічуються. Кажуть, що схема діє як фільтр, фільтруючи вихідний сигнал на основі частоти кожного компонента комплексної експоненціальної. Оскільки низькі частоти проходять через фільтр, ми називаємо його фільтром низьких частот, щоб точніше висловити його функцію.

Ми також виявили простоту обчислення виходу для синусоїдальних входів за допомогою функції передачі. Як тільки ми знайдемо функцію передачі, ми можемо записати вихід безпосередньо, як зазначено виходом схеми для синусоїдального входу.

Приклад\(\PageIndex{1}\):

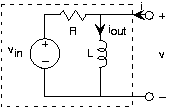
Давайте застосуємо ці результати до остаточного прикладу, в якому вхід є джерелом напруги, а на виході - струм індуктивності. Напруга джерела дорівнює:

\[V_{in}=2\cos (2\pi 60t)+3 \nonumber \]

Ми хочемо, щоб ланцюг пропускав постійну (зміщену) напругу по суті незмінним (за винятком того, що на виході є струм, а не напруга) і прибираємо термін 60 Гц. Оскільки вхід - це сума двох синусоїдів - константа - косинус нульової частоти - наш підхід

знайти функцію передачі за допомогою імпедансів
використовувати його, щоб знайти вихід завдяки кожному вхідному компоненту
додати результати
знайти значення елементів, які відповідають нашим критеріям проектування

_{Оскільки схема являє собою послідовну комбінацію елементів, давайте використовувати дільник напруги, щоб знайти функцію передачі між V і V, а потім використовувати v-i відношення індуктора, щоб знайти його струм.}

\[\frac{I_{out}}{V_{in}}=\frac{i2\pi fL}{R+i2\pi fL}\frac{1}{i2\pi fL} \nonumber \]

\[\frac{I_{out}}{V_{in}}=\frac{1}{i2\pi fL+R} \nonumber \]

\[\frac{I_{out}}{V_{in}}=H(f) \nonumber \]

де дільник напруги

\[voltage\; \; divider=\frac{i2\pi fL}{R+i2\pi fL} \nonumber \]

\[inductor\; \; admittance=\frac{1}{i2\pi fL} \nonumber \]

[Чи перевіряють одиниці?] Форма цієї функції передачі повинна бути знайомою; це фільтр низьких частот, і він буде виконувати нашу бажану функцію, як тільки ми правильно виберемо значення елементів.

З постійним терміном найлегше впоратися. Вихідні дані задаються:

\[3\left | H(0) \right |=\frac{3}{R} \nonumber \]

Таким чином, значення, яке ми вибираємо для опору, буде визначати коефіцієнт масштабування того, як напруга перетворюється в струм. Для компонентного сигналу 60 Гц вихідний струм дорівнює

\[2\left | H(60) \right |\cos \left ( 2\pi 60t+\angle (H(60)) \right ) \nonumber \]

Загальний вихід завдяки нашому джерелу:

\[i_{out}=2\left | H(60) \right |\cos \left ( 2\pi 60t+\angle (H(60)) \right )+3\times H(0) \nonumber \]

Частота зрізу для цього фільтра виникає, коли дійсна і уявна частини знаменника передавальної функції дорівнюють один одному. Таким чином,

\[2\pi f_{c}L=R \nonumber \]

\[f_{c}=\frac{R}{2\pi L} \nonumber \]

Ми хочемо, щоб ця частота зрізу була набагато менше 60 Гц. Припустимо, ми розміщуємо його на, скажімо, 10 Гц. Ця специфікація вимагатиме, щоб значення компонентів були пов'язані

\[\frac{R}{L}=20\pi =62.8 \nonumber \]

Функція передачі при 60 Гц буде

\[\left | \frac{1}{i2\pi 60L+R} \right |=\frac{1}{R}\left | \frac{1}{6i+1} \right |=\frac{1}{R}\frac{1}{\sqrt{37}}\simeq 0.16\times \frac{1}{R} \nonumber \]

який дає загасання (щодо посилення на нульовій частоті) близько 1/6, і призводить до вихідної амплітуди 0.3/R відносно амплітуди постійного члена 3/R. коефіцієнт відносного розміру 10 між двома компонентами здається розумним. Маючи індуктор 100 мГн вимагатиме резистора 6.28 Ом. Легко доступне значення резистора становить 6,8 Ом; таким чином, цей вибір призводить до дешевих і легко придбаних деталей. Щоб зробити опір більшим, потрібно пропорційно більший індуктор. На жаль, навіть індуктор 1 Н фізично великий; отже, низькі частоти зрізу вимагають малозначних резисторів і великоцінних індукторів. Зроблений тут вибір являє собою лише один компроміс.

Фаза 60 Гц складова буде дуже майже -π/2 залишаючи її:

\[\frac{0.3}{R}\cos \left ( 2\pi 60t-\frac{\pi }{2} \right )=\frac{0.3}{R}\sin (2\pi 60t) \nonumber \]

Форми хвиль для входу та виходу показані нижче:

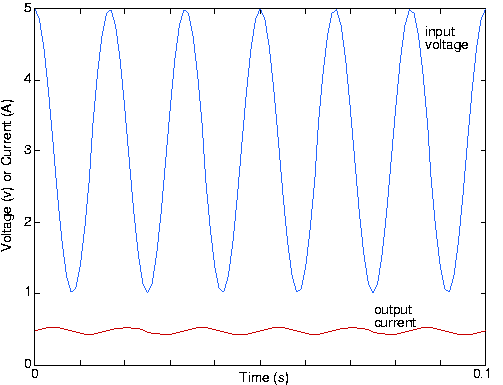
Малюнок 3.14.2: Форми вхідних та вихідних сигналів для прикладу *схеми RL, коли значення елементів є* **R = 6.28** Ом і **L = 100mH**

Зверніть увагу, що фаза синусоїди дійсно змістилася; фільтр низьких частот не тільки зменшив амплітуду сигналу 60 Гц, але й змістив його фазу на 90°.