1.13: Молекулярна спектроскопія

Наші найбільш детальні знання про атомну та молекулярну структуру були отримані в результаті спектроскопічного дослідження випромінювання, поглинання та розсіювання електромагнітного випромінювання, що супроводжує переходи між рівнями атомної або молекулярної енергії. Тоді як атомні спектри включають лише електронні переходи, спектроскопія молекул є більш складною, оскільки вібраційні та обертальні ступені свободи також вступають у гру. Ранні спостереження за поглинанням або випромінюванням молекулами характеризувалися як смуговий спектр на відміну від лінійних спектрів, виставлених атомами. Тепер зрозуміло, що ці смуги відображають тісно розташовані вібраційні та обертальні енергії, що підсилюють електронні стани молекули. З поліпшенням спектроскопічних методів протягом багатьох років стало можливим вирішення окремих коливальних і обертальних переходів. Це дало багате джерело інформації про молекулярну геометрію, енергетику та динаміку. Молекулярна спектроскопія також внесла значний внесок у аналітичну хімію, науку про навколишнє середовище, астрофізику, біофізику та біохімію.

Знижена маса

Розглянемо систему з двох частинок мас\(m_1\) і\(m_2\) взаємодіючих з потенційною енергією, яка залежить тільки від поділу частинок. Класична енергія задається точками\[E=\frac{1}{2} m_1 \dot{\vec{r}}_1^2+\frac{1}{2} m_2 \dot{\vec{r}}_2^2+V (|\vec{r}_2-\vec{r}_1|) \label{1}\], що позначають похідну wrt час. Ввести дві нові змінні, поділ частинок\(\vec{r}\) і положення центру маси\(\vec{R}\):

\[ \vec{r}=\vec{r}_2-\vec{r}_1 \mbox{,}\hspace{20pt}\vec{R}=\dfrac{m_1 \vec{r}_1+m_2\vec{r}_2}{m}\label{2}\]

де\(m=m_1+m_2\). З точки зору нових координат

\[\vec{r}_1=\vec{R}+\frac{m_2}{m} \vec{r} \mbox{,}\hspace{20pt}\vec{r}_2=\vec{R}-\frac{m_1}{m} \vec{r}\label{3}\]

і

\[E=\dfrac{1}{2}m\dot{\vec{R}}^2+\dfrac{1}{2}\mu\dot{\vec{r}}^2+V(r)\label{4}\]

де\(r=|\vec{r}|\) і\(\mu\) називається\(reduced\hspace{2pt}mass\)

\[\mu\equiv\dfrac{m_1 m_2}{m_1+m_2}\label{5}\]

Альтернативним співвідношенням для зниженої маси є

\[\dfrac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2}\label{6}\]

нагадує формулу опору паралельного контуру. Зверніть увагу, що, якщо\(m_2\rightarrow\infty\), то\(\mu\rightarrow m_1\). Термін, що містить,\(\dot{\vec{R}}\) являє собою кінетичну енергію однієї гіпотетичної частинки маси,\(\mu\) розташованої в центрі мас\(\vec{R}\). Решта члени представляють\(relative\) рух двох частинок. Це була поява\(single\) частинки ефективної маси, що\(\mu\) рухається в потенційному полі\(V(r)\).

\[E_{rel}=\dfrac{1}{2} \mu \dot{\vec{r}^2}+V(r)= \dfrac{\vec{p}^2}{2\mu}+V(r)\label{7}\]

Таким чином, ми можемо записати рівняння Шредінгера для відносного руху.

\[ \left\{-\dfrac{\hbar^2}{2 \mu} \bigtriangledown^2+V(r) \right\}\psi (\vec{r})= E \psi (\vec{r}) \label{8}​\]

Коли ми лікували атом водню, передбачалося, що ядерна маса нескінченна. У такому випадку ми можемо встановити\(\mu =m\) масу електрона. Константа Рідберга для нескінченної ядерної маси обчислювалася як

\[R_\infty = \dfrac{2\pi^2me^4}{h^3c}=109,737 \text{cm} ^{-1}\label{9}\]

Якщо замість цього використовувати зменшену масу електронно-протонної системи

\[\mu = \dfrac{mM}{m+M} \approx \dfrac{1836}{1837}\, m \approx 0.999456 \, m \label{10}\].

Це змінює постійну Рідберга для водню на

\[R_{H}\approx 109,677 \, cm^{-1}\label{11}\]

в ідеальному узгодженні з експериментом.

У 1931 році Юрі випаровував чотири літри водню до одного мілілітра і виміряв спектр залишку. В результаті вийшла сукупність ліній, трохи зміщених від водневого спектра. Це склало відкриття дейтерію, або важкого водню, за що Юрі був удостоєний в 1934 році Нобелівської премії з хімії. Оцінюючи масу дейтрона, ² Н ₁, як удвічі більше протона, дає

\[R_{D}\approx 109,707 \, cm^{-1}\label{12}\]

Інший цікавий приклад, що включає зменшену масу, стосується позитронію, короткочасної комбінації електрона та античастинки позитрона-електрона. Електрон і положення взаємно анігілюються з періодом напіврозпаду приблизно 10 ^-7 сек. і позитрій розпадається на гамма-промені. Знижена маса позитронію становить

\[ \mu = \frac{m \times m}{m+m} = \frac{m}{2} \label{13} \]

половину маси електрона. Таким чином, енергія іонізації дорівнює 6,80 еВ, вдвічі менше атома водню. Позитронно-емісійна томографія (ПЕТ) забезпечує чутливу техніку сканування для функціонування живої тканини, зокрема мозку. В організм вводиться з'єднання, що містить позитрон-випромінюючий радіонуклід, наприклад, ¹¹ С, ¹³ Н, ¹⁵ О або ¹⁸ Ф. Випромінювані позитрони приєднуються до електронів, утворюючи короткочасний позитроній, а аннігіляційне випромінювання контролюється.

Вібрація двоатомних молекул

Двоатомна молекула з ядерними масами M, _A, M _B має зменшену масу.

\[\mu =\frac{M_{A}M_{B}}{M_{A}+M_{B}}\label{14}\]

Розв'язок електронного рівняння Шредінгера дає енергію як функцію міжядерної відстані E _elec (R). Це відіграє роль потенційної енергетичної функції для руху ядер V (R), як намальовано на рис.2. Таким чином, ми можемо записати рівняння Шредінгера для вібрації.

\ [\ почати {Bmatrix}
-\ frac {\ hbar^2} {2\ му}\ frac {d^2} {dr^2} +V (R)\ кінець {Bmatrix}\ chi (R) =E_ {\ chi} (R)\ мітка {15}\]

Якщо потенційна енергія розширена в серії Тейлора про R = R _e

\[V(R)=V(R_{e})+(R-R_{e})V'(R_{e})+\frac{1}{2}(R-R_{e})^2V"(R_{e})+...\label{16}\]

Апроксимація для цього розширення має вигляд гармонічного осцилятора з

\[V(R)\approx \frac{1}{2}k(R-R_{e})^2\label{17}\]

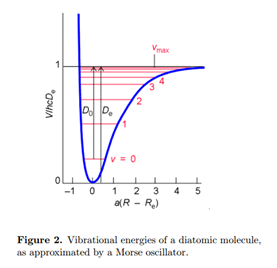
Походження енергії можна вибрати так V (R _e) = 0. При мінімумі потенціалу V' (R _e) = 0. Найкраще прилягання до параболи (17) виходить з постійною силою, встановленою рівною

\[k\approx \frac{d^2V(R)}{dR^2}\mid _{R\, =\, R_{e}}\label{18}\]

З розв'язку для гармонічного осцилятора ми ідентифікуємо коливальну енергію стану землі, з квантовим числом\(\nu\) = 0

\[E_{0}=\hbar\omega =\hbar\sqrt{\frac{k}{\mu }}\label{19}\]

Фактична енергія дисоціації з наземного коливального стану наближається

\[D_{0}\approx D_{e}-\frac{1}{2}\hbar\omega\label{20}\]

У хвильових одиницях

\[hcD_{0}\approx hcD_{e}-\frac{1}{2}\tilde{\nu }\: cm^{-1}\label{21}\]

Покращена обробка молекулярної вібрації повинна враховувати ангармонічність, відхилення від гармонічного осцилятора. Ангармонічність призводить до кінцевої кількості коливальних енергетичних рівнів і можливості дисоціації молекули при досить високій енергії. Дуже вдалим наближенням для енергії двоатомної молекули є потенціал Морзе:

\[V(R)=hcD_{e}\begin{Bmatrix}1-e^{a(R-R_{e})}\end{Bmatrix}^2\; \; \; a=\begin{pmatrix}\frac{\mu \omega ^2}{2hcD_{e}}\end{pmatrix}^{\frac{1}{2}}\label{22}\]

Зверніть увагу, що V (R _e) = 0 при мінімумі потенційної ями. Рівняння Шредінгера для генератора Морзе може бути розв'язано для отримання енергетичних рівнів

\[E_{\upsilon }=(\upsilon +\frac{1}{2})\hbar\omega-(\upsilon+\frac{1}{2} )^2\hbar\omega x_{e}\label{23}\]

або, виражені в хвильових числових одиницях,

\[hcE_{\upsilon }=(\upsilon +\frac{1}{2})\tilde{\nu }-(\upsilon +\frac{1}{2})^2x_{e}\tilde{\nu }\label{24}\]

Більш високі коливальні рівні енергії розташовані ближче один до одного, так само, як і в реальних молекулах. Коливальні переходи двоатомних молекул відбуваються в інфрачервоному діапазоні приблизно в межах 50-12 000 см ^-1. Молекула буде поглинати або випромінювати випромінювання тільки в тому випадку, якщо вона має ненульовий дипольний момент. Таким чином, HCl є інфрачервоним активним, тоді як H ₂ і Cl ₂ - ні.

Вібрація багатоатомних молекул

Молекула з атомами N має загалом 3N ступенів свободи для своїх ядерних рухів, оскільки кожне ядро може самостійно зміщуватися в трьох перпендикулярних напрямках. Три з цих ступенів свободи відповідають поступальному руху центру мас. Для нелінійної молекули ще три ступені свободи визначають орієнтацію молекули в просторі, і, таким чином, її обертальний рух. Це залишає 3N - 6 коливальних режимів. Для лінійної молекули існує відразу дві обертальні ступені свободи, що залишає 3N - 5 коливальних режимів. Наприклад, нелінійна молекула H ₂ O має три коливальних режими, тоді як лінійна молекула СО ₂ має чотири коливальні режими. Вібрації складаються з скоординованих рухів декількох атомів таким чином, щоб центр мас тримався нерухомим і необертовим. Вони називаються нормальними режимами. Кожен нормальний режим має характерну резонансну частоту\(\tilde{\nu _{i}}\), яка зазвичай визначається експериментальним шляхом. До розумного наближення кожен нормальний режим поводиться як незалежний гармонічний генератор частоти\(\tilde{\nu _{i}}\). Нормальні режими H ₂ O і CO ₂ зображені нижче.

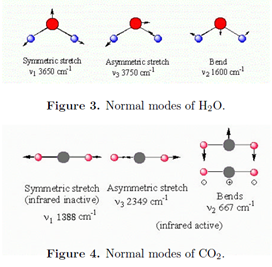
Нормальний режим буде інфрачервоним активним тільки в тому випадку, якщо він передбачає зміну дипольного моменту. Всі три режими H ₂ O активні. Симетрична розтяжка СО ₂ неактивна, оскільки дві C-O зв'язки, кожна з яких полярна, точно компенсують. Зверніть увагу, що режим згинання СО ₂ подвійно вироджується. Згинання сусідніх зв'язків у молекулі, як правило, включає менше енергії, ніж розтягнення зв'язку, таким чином, режими згинання, як правило, мають менші хвильові числа, ніж режими розтягування.

Обертання двоатомних молекул

Модель жорсткого ротора передбачає, що міжядерна відстань R є постійною. Це не погане наближення, оскільки амплітуда вібрації, як правило, становить близько 1% від R. Рівняння Шредінгера для ядерного руху потім включає тривимірний оператор кутового моменту, написаний,\(\hat{J}\) а не тоді,\(\hat{L}\) коли він стосується молекулярного обертання. Розв'язки цього рівняння вже відомі, і ми можемо записати

\[\frac{\hat{J}^2}{2\mu R^2}Y_{JM}(\theta ,\phi )=E_{J}Y_{JM}(\theta,\phi)\; \; \; J=0,1,2...\; \; \; M=0,\pm \, 1...\pm\,J\label{25}\]

де Y _JM (\(\theta,\phi\)) - сферичні гармоніки через квантові числа J і M, а не l і m. Оскільки власні значення\(\hat{J}^2\) є\(J(J +1)\hbar^2\), рівні енергії обертання є

\[E_{J}=\frac{\hbar^2}{2I}J(J+1)\label{26}\]

Момент інерції задається

\[I=\mu R^2=M_{A}R^{2}_{A}+M_{B}R^{2}_{B}\label{27}\]

де R _A і R _B - відстані від ядер A і B відповідно до центру мас. В одиницях хвильового числа виражається енергія обертання

\[hcE_{J}=BJ(J+1)cm^{-1}\label{28}\]

де B - постійна обертання. Діаграма обертального рівня енергії показана на рис.5. Кожен рівень (2J + 1) -кратний вироджений. Знову ж таки, тільки полярні молекули можуть поглинати або випромінювати випромінювання в ході обертальних переходів. Випромінювання знаходиться в мікрохвильовій або далекій інфрачервоній області. Правило вибору для обертальних переходів -\(\Delta\) J =\(\pm\) 1.

Молекулярні параметри з спектроскопії

Нижче наведена таблиця спектроскопічних констант для чотирьох галогенідів водню:

Константу сили можна знайти з коливальної постійної. Прирівнюючи енергетичні величини\(\hbar\omega=hc\tilde{\nu }\), знаходимо

\[\omega=2\pi c\tilde{\nu }=\sqrt{\frac{k}{\mu }}\label{29}\]

Таким чином

\[k=(2\pi c\tilde{\nu })^2\mu\label{30}\]

із

\[\mu=\frac{m_{A}m_{B}}{m_{A}+m_{B}}=\frac{M_{A}M_{B}}{M_{A}+M_{B}}u\label{31}\]

де u = 1,66054 х 10 ^-27 кг, одиниця атомної маси. M _A і M _B - умовні атомні ваги атомів A і B (за шкалою ¹² C = 12). Введення числових факторів

\[k=58.9\, \times \, 10^{-6}(\tilde{\nu }/cm^{-1})^2\frac{M_{A}M_{B}}{M_{A}+M_{B}}N/m \label{32}\]

Це дає 958,6, 512,4, 408,4 і 311,4 Н/м для HF, HCl, HBr і HI відповідно. Ці значення не враховують ангармонійність.

Міжядерна відстань R визначається постійною обертання. За визначенням,

\[hcB=\frac{\hbar^2}{2I}\label{33}\]

Таким чином

\[B=\frac{\hbar}{4\pi cI}\label{34}\]

із

\[I=\mu R^2=\frac{m_{A}m_{B}}{m_{A}+m_{B}}R^2=\frac{M_{A}M_{B}}{M_{A}+M_{B}}uR^2\; \; kg\: m^2\label{35}\]

Рішення для R,

\[R=410.6 / \sqrt{\frac{M_{A}M_{B}}{M_{A}+M_{B}}(B/cm^{-1})}\: \: pm\label{36}\]

Для галогенідів водню HF, HCl, HBr, HI обчислюємо R = 92,0, 127,9, 142,0, 161,5 пм відповідно.

Обертання нелінійних молекул

Нелінійна молекула має три моменти інерції близько трьох головних осей, позначені I _a, I _b і I _c. Класичну енергію обертання можна записати

\[E=\dfrac{J^2_{a}}{2I_{a}}+\frac{J^2_{b}}{2I_{b}}+\dfrac{J^2_{c}}{2I_{c}}\label{37}\]

де J _a, J _b, J _c - складові моменту навколо головних осей. Для сферичного ротора, такого як CH ₄ або SF ₆, три моменти інерції рівні однаковому значенню I. Енергія спрощується до J ^2/2I, а квантово-механічний гамільтоніан задається

\[\hat{H}=\frac{\hat{J}^2}{2I}\label{38}\]

До власних значень

\[E_{J}=\frac{\hbar^2}{2I}J(J+1)\; \;\; J=0,1,2..\label{39}\]

так само, як для лінійної молекули. Але рівні сферичного ротора мають виродженняз (2 J + 1) ², а не (2 J + 1).

Симетричний ротор має два рівних моменту інерції, скажімо I _c = I _{b\(\neq \)} I _a. Молекули NH ₃, CH ₃ Cl і C ₆ H ₆ є прикладами. Гамільтоніан набуває форми

\[ \hat H = \frac{\hat J_a^2}{2I_a}+\frac{\hat J_b^2 + \hat J_c^2}{2I_b} = \frac{\hat J^2}{2I_b} + (\frac{1}{2I_a} - \frac{1}{2I_b}) \hat J_a^2 \label{40} \]

Оскільки можливе одночасне володіння\(\hat J^2\) власнимистанами і однієї з його складових\(\hat J_a\), енергії симетричного ротора мають вигляд.

\[E_{JK}=\frac{J(J+1)}{2I_{b}}+(\frac{1}{2I_{a}}-\frac{1}{2I_{b}})K^2\; \; J=0,1,2...\; \;\; K=0\pm 1,\pm2,...\pm J\label{41}\]

Існує, крім того, (2 J + 1) -кратна M виродження.

Електронні збудження в двоатомних молекулах

Квантові стани молекул - це композити обертального, коливального та електронного внесків. Енергетичні інтервали, характерні для цих різних ступенів свободи, змінюються на багато порядків, породжуючи дуже різні спектроскопічні методи дослідження обертальних, коливальних та електронних переходів. Електронні збудження зазвичай мають порядок декількох електронвольт, 1 еВ еквівалентний приблизно 8000 см ^-1 або 100 кДж моль ^-1. Як ми бачили, типові енергетичні відмінності становлять близько 1000 см ^-1 для вібрації і 10 см ^-1 для обертання. Рис. 6 дає загальне уявлення про відносні величини цих енергетичних внесків. Кожне електронний стан має коливальну структуру, характеризується коливальними квантовими числами v і кожне коливальний стан має обертальну структуру, що характеризується обертальними квантовими числами J і M.

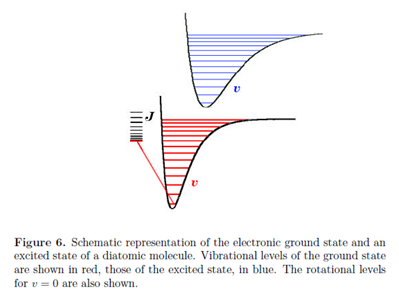
Кожен електронний перехід в молекулі супроводжується змінами коливального і обертального станів. Як правило, в рідкому стані окремі коливальні переходи не вирішуються, так що електронні спектри складаються з широких смуг, що містять велику кількість перекриваються коливальних і обертальних переходів. Спектроскопія на газовій фазі, однак, часто може вирішити окремі коливальні і навіть обертальні переходи.

Коли молекула піддається переходу в інший електронний стан, електрони переставляються набагато швидше, ніж ядра. До дуже хорошого наближення електронний стан можна вважати, що відбувається миттєво, тоді як ядерна конфігурація залишається фіксованою. Це відоме як принцип Франка-Кондона. Він має таке ж фізичне походження, як і наближення Борна-Оппенгеймера, а саме велику нерівність в електронних і ядерних масах. На діаграмі, що показує енергії землі та збуджених станів як функції міжядерної відстані, поведінка Франка-Кондона характеризується вертикальними переходами, при яких R залишається приблизно постійним у міру переходу молекули з однієї потенційної кривої на іншу.

У коливальному стані\(\upsilon \) = 0 максимум ймовірності для міжядерної відстані R знаходиться поблизу центру потенційної ямки. При всіх вищих значеннях коливальних станів максимуми ймовірності виникають поблизу двох поворотних точок потенціалу - де сумарна енергія дорівнює потенційній енергії. Вони відповідають на діаграмах кінцевим точкам горизонтальних рисок всередині кривої потенціалу.

Дописувачі та авторства

Template:ContribBlinder