2.2: Групи точок
- Page ID
- 18433
Групи точок низької симетрії
C 1 Група точок
Загалом, ми розділимо групи точок на три основні категорії: групи точок високої симетрії, групи точок низької симетрії, двогранні групи точок та групи обертальних точок. Почнемо з груп точок низької симетрії. Як випливає з назви, ці групи точок мають лише кілька елементів симетрії та операцій. Точкова група С 1 - це група точок з найменшою симетрією. Молекули, що належать до цієї групи точок, мають ідентичність лише як елемент симетрії.
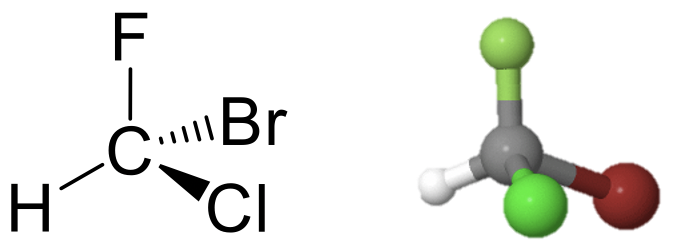
Прикладом може служити молекула бромхлорфлурометану (рис.2.2.1). У ньому немає елемента симетрії, а ідентичності. Назва C 1 походить від елемента симетрії C 1. Операція C 1 така ж, як і ідентичність.
C s Точкова група
Точкова група C s має дзеркальну площину на додаток до ідентичності. Прикладом може служити молекула 1,2-бромхлоретену (рис.2.2.2).
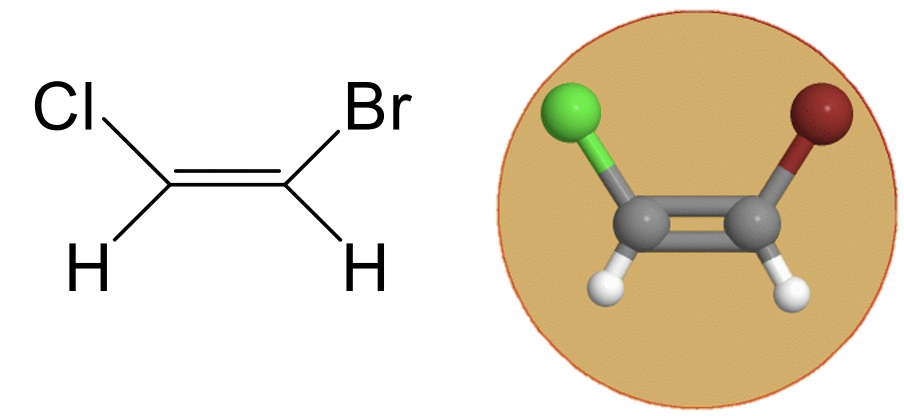Малюнок 2.2.2 C s точка групи 1, 2-бромхлоретену (Зазначення авторства: symotter.org/gallery)Це плоска молекула, а дзеркальна площина знаходиться в межах площини молекули. Ця дзеркальна площина не рухає жодних атомів, коли виконується операція відбиття, проте вона існує, оскільки будь-яка точка молекули над дзеркальною площиною буде знайдена нижче площини дзеркала після виконання операції. Навпаки, будь-яка точка нижче дзеркальної площини буде знаходитися над дзеркальною площиною. Ця дзеркальна площина не має вертикального або горизонтального позначення площини дзеркала, оскільки не існує належних осей обертання.
C і точка Група
Точкова група C i має інверсію як єдиний елемент симетрії, окрім ідентичності. Точкову групу C i іноді також називають S 2, оскільки неправильне обертання-відображення S 2 таке ж, як інверсія. Прикладом може служити 1,2-дибромо 1,2-дихлоретан (рис.2.2.3).
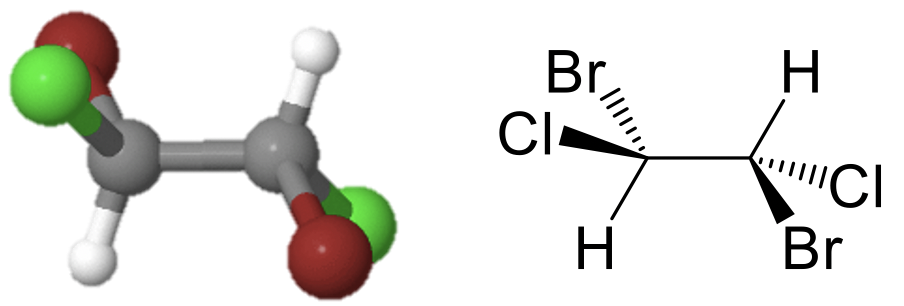
Ця молекула виглядає досить симетрично, але вона має інверсійний центр посередині вуглецево-вуглецевого зв'язку як єдиний елемент симетрії. Після виконання операції інверсії два вуглеці міняються своїми позиціями, так само як і два брому, два хору, і два атоми водню.
Групи точок високої симетрії
Елементи симетрії груп точок високої симетрії можна легше зрозуміти, коли спочатку розуміються властивості платонічних твердих тіл. Платонічні тверді тіла - це багатогранники, складені з правильних багатокутників. У платонічному твердому тілі всі грані, ребра і вершини (кути) симетрично еквівалентні. Ми побачимо, що це властивість, яку можна використовувати для розуміння елементів симетрії в групах точок високої симетрії. Існує лише п'ять можливостей зробити платонічні тверді тіла з правильних багатокутників (рис.2.2.4).
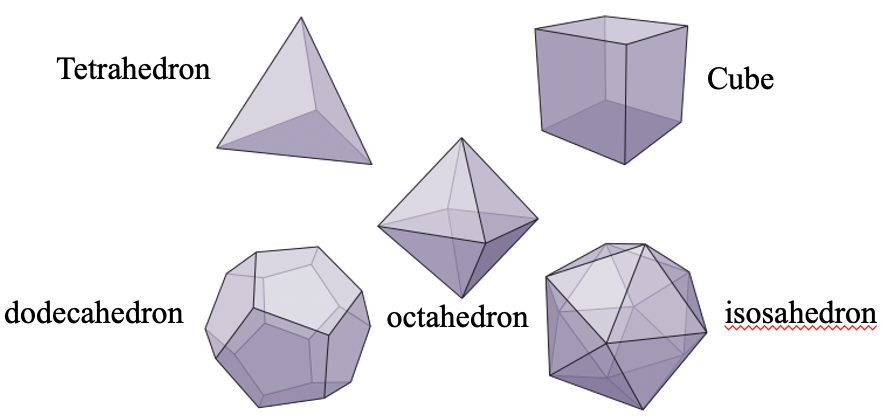
Перша можливість - побудувати тетраедр з чотирьох правильних трикутників. Друге платонічне тверде тіло - це октаедр, виконаний з восьми правильних трикутників. Третя можливість - ікосаедр, зроблений з двадцяти трикутників. Крім того, шість квадратів можна з'єднати, утворюючи куб, а дванадцять п'ятикутників можуть бути з'єднані, утворюючи додекаедр. Немає можливості з'єднати інші правильні багатокутники, такі як шестикутники, щоб зробити платонічне тверде тіло.
Ікосаедр є найскладнішим з усіх платонічних твердих тіл. Якщо ви хочете побачити і вивчити ікосаедр ззовні і всередині, є один для вивчення на дитячому майданчику парку Allentown Cedar Beach Park, в Аллентауні, штат Пенсільванія.
Точкова група T d
Тетраедр, а також чотиригранні молекули і аніони типу CH 4 і BF 4 - відносяться до групи точок високої симетрії Т d. Знайдемо елементи симетрії та операції симетрії, які належать до групи точок T d. По-перше, ми не повинні забувати про операцію ідентичності, тобто далі корисно шукати основні осі.
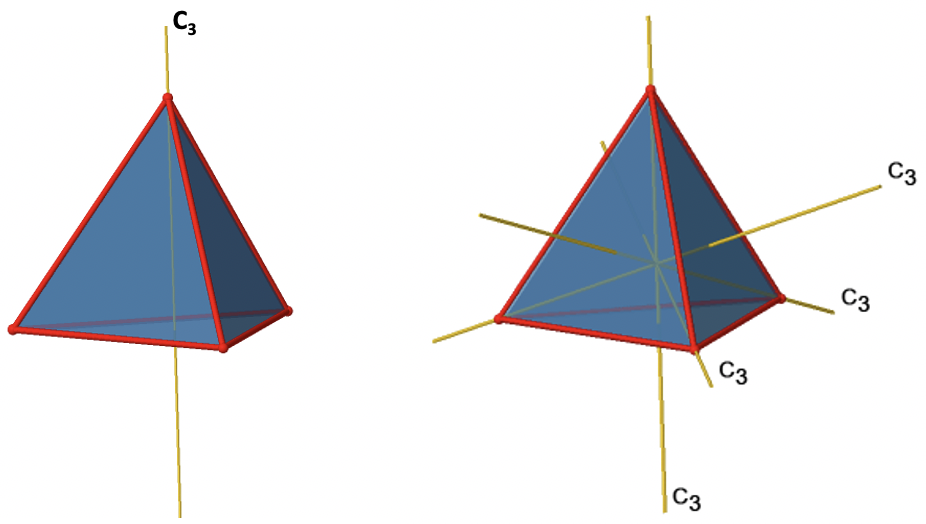
Тетраедр має чотири головні осі С 3 (рис.2.2.6). Це властивість груп точок високої симетрії, що вони мають більше однієї головної осі. Осі С 3 проходять через вершини тетраедра. Оскільки кожна вісь C 3 проходить через одну вершину, є чотири вершини, і ми знаємо, що в платонічному твердому тілі всі вершини еквівалентні симетрії, ми можемо зрозуміти, що є чотири осі C 3. Скільки унікальних операцій C 3 пов'язано з цими осями? Після трьох обертань навколо 120° ми досягаємо ідентичності. Тому C 3 3 = E, і нам потрібно тільки розглянути C 3 1 і C 3 2 обертання приблизно 120 і 240° відповідно. Оскільки є чотири осі C 3, є чотири C 3 1 і чотири операції C 3 2 і вісім операцій C 3 в цілому. Ми можемо висловити це, написавши відповідні числа у вигляді коефіцієнтів перед символом Шенфліє для операцій (рис. 2.2.7).
Крім осей С 3 є осі С 2 (рис.2.2.8).
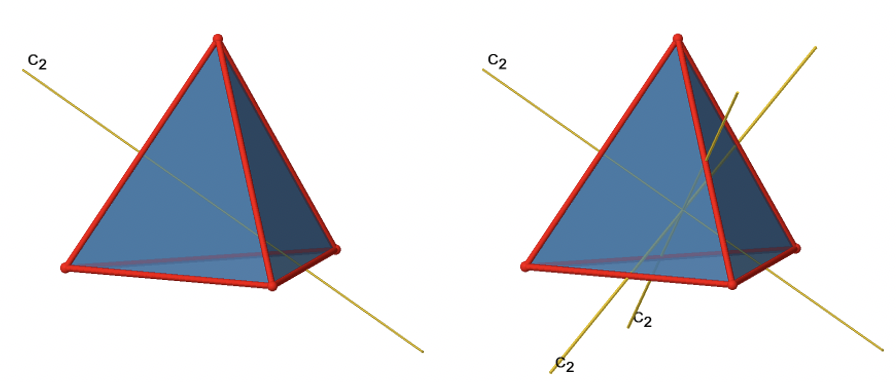
Ви можете бачити, що вісь C 2 проходить через два протилежних краю в тетраедрі. Оскільки тетраедр має шість ребер, а кожна вісь C 2 проходить через два ребра, є осі 6/2 = 3 C 2. Існує лише одна операція симетрії C 2 на осі C 2, оскільки ми створюємо ідентичність вже після двох обертань. Тому існує три операції С 2 1 в цілому (рис.2.2.9).
Крім того, група точок T d має S 4 неправильні відображення обертання. Як і осі С 2, вони проходять через середину двох протилежних країв. Це також означає, що вони накладають осі С 2. Оскільки є шість ребер, а дві осі S 4 на ребро є 6/2 = 3 S 4 осі (рис. 2.2.10).
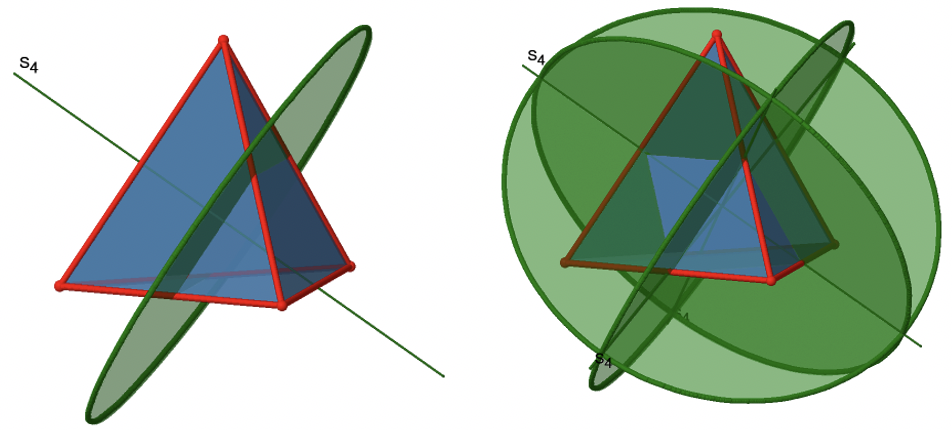
Скільки операцій пов'язано з цими осями S 4? Порядок осей парний, і тому нам потрібно чотири операції S 4 для отримання ідентичності. Операція S 4 2 така ж, як операція C 2 1, оскільки відображення два рази еквівалентно взагалі не відображати, а обертання два рази на 90° - це те саме, що і обертання близько 180°. Тому в цілому тільки операції S 4 1 і S 4 3 є унікальними операціями. S 4 2 і S 4 4 можуть бути виражені більш простими операціями C 2 1 і E відповідно. Оскільки є 3 S 4 осі, є три S 4 1 і три операції S 4 3. Всього існує шість операцій S 4 (рис. 2.2.11).
Існують і дзеркальні площини (рис.2.2.11). Площини містять єдиний край тетраедра, тим самим розсікаючи тетраедр. У тетраедрі шість ребер, і тому є дзеркальні площини 6/1 = 6.
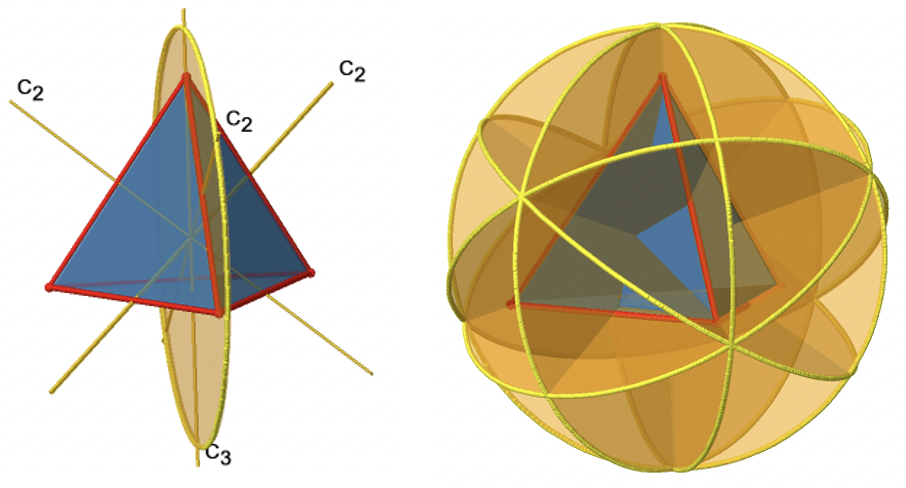
Ці площини є двогранними площинами, оскільки кожна площина містить головну вісь C 3 і бісекції кута між двома осями C 2. Загалом, є три осі C 2 і три операції C 2. Існує одна операція відображення на площині дзеркала, оскільки відображення два рази виробляє ідентичність. Тому існує шість σ d операцій відображення (рис. 2.2.12, праворуч і рис. 2.2.13).
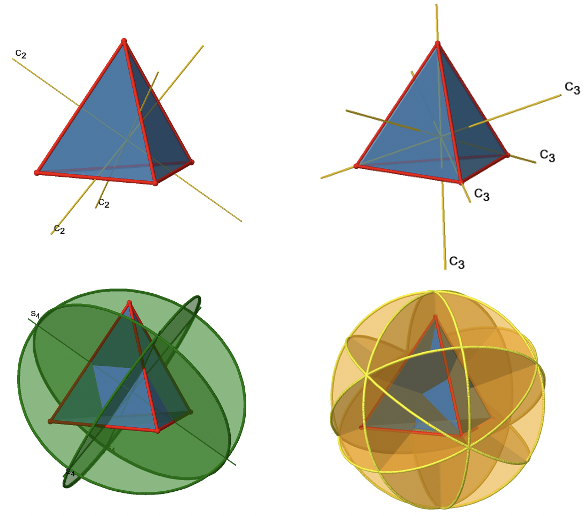
У сумі (рис.2.2.14 і 2.2.15) загальну симетрію групи T d ми можемо позначити наступним чином: Е, 8С 3, 3С 2, 6S 4, 6σ d. Детально унікальними операціями симетрії є E, 4C 3 1, 4C 3 2, 3C 2 1, 3S 4 1, 3S 4 3, 6σ d.
Обертальна підгрупа T
Точкова група високої симетрії Т - це так звана обертальна підгрупа точкової групи T d. Ротаційна підгрупа - це група точок, в якій усі операції симетрії, крім ідентичності та належних обертань, були вилучені з групи точок високої симетрії. Для групи точки Т це залишає 4С 3, чотири С 3 2 і три операції С 2 (рис. 2.2.17). S 4 обертання-відбиття та дзеркальні площини були видалені. Точкова група Т зустрічається рідко.
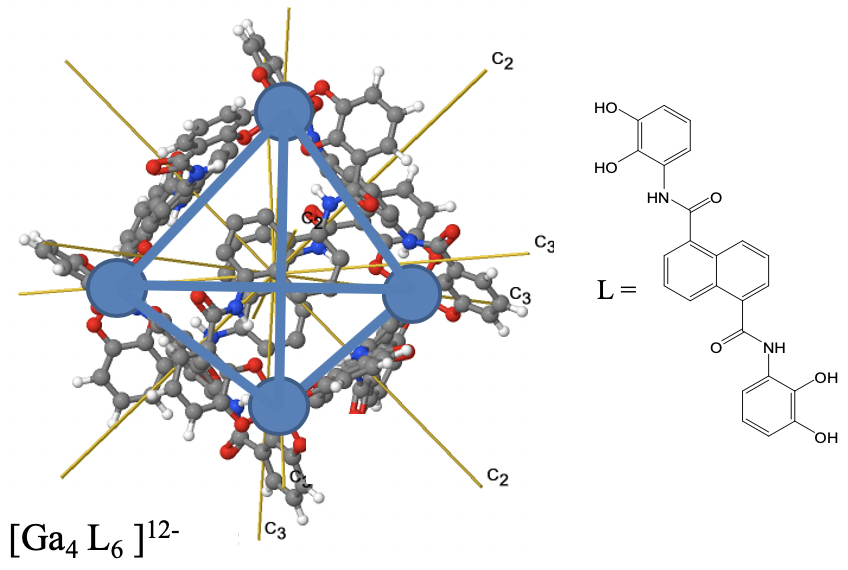
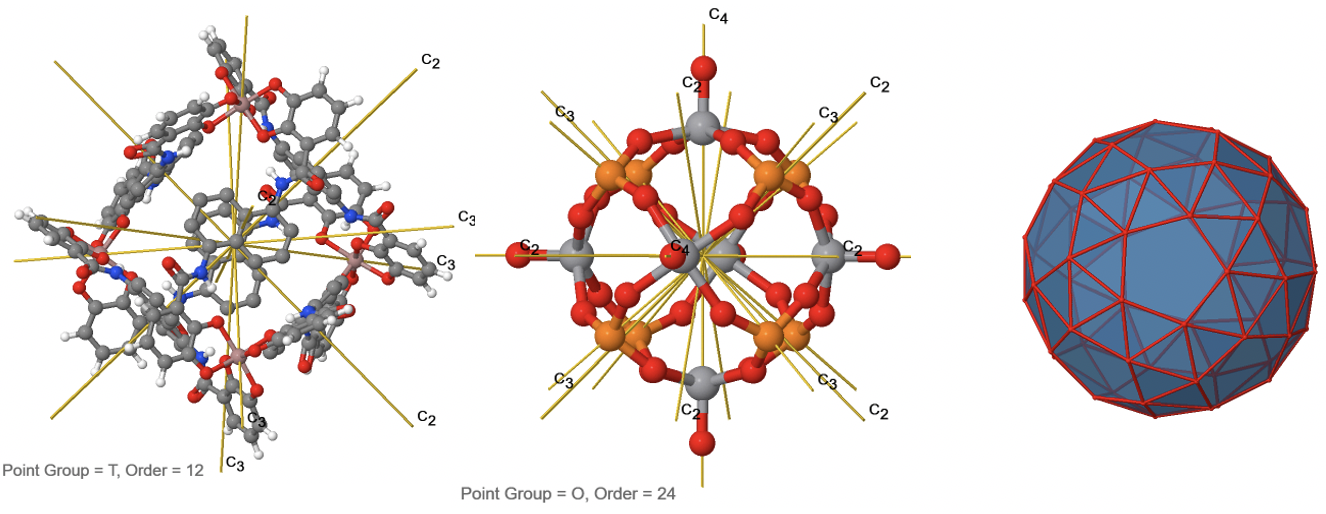
Прикладом може служити зображена клітка Ga 4 L 6 (рис.2.2.16). Атоми Ga займають вершини тетраедра, але точкова група не T d, а T через форму лігандів, які з'єднують чотири атоми Ga.
Октаедрична точка група O h
Ще однією групою точок високої симетрії є група точок O h. І октаедр, і куб належать до цієї точкової групи, незважаючи на їх дуже різну форму (рис.2.2.18). Оскільки вони належать до однієї групи точок, вони повинні мати однакові елементи симетрії та операції. Існує багато молекул октаедральної форми, таких як SF 6.
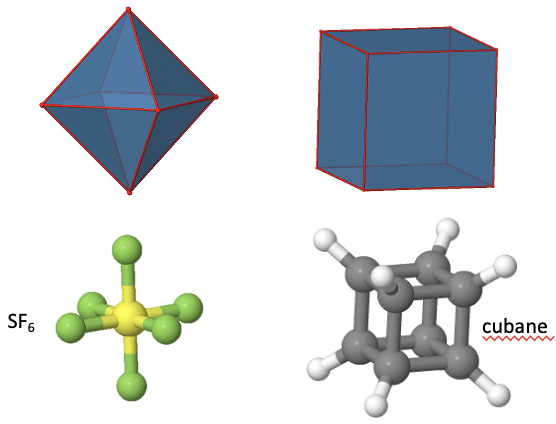
Молекули з кубічними формами зустрічаються набагато рідше, тому що кубічна форма часто призводить до значного деформації молекули. Прикладом може служити кубан С 8 Н 8. Визначимо елементи симетрії і операції для точкової групи O h на прикладі октаедра. Якби ми використовували куб, ми отримали б точно такі ж результати.
У октаедрі є три головні осі С 4. Вони проходять через дві протилежні вершини октаедра (рис.2.2.19). Є три осі C 4, оскільки октаедр має шість вершин, які всі симетричні еквівалентні, оскільки октаедр є платонічним твердим тілом.
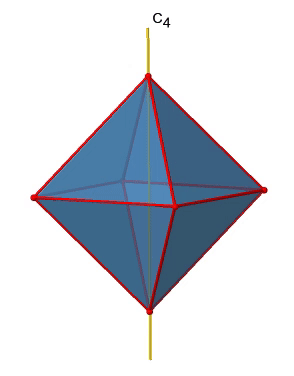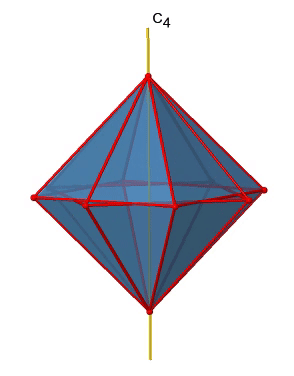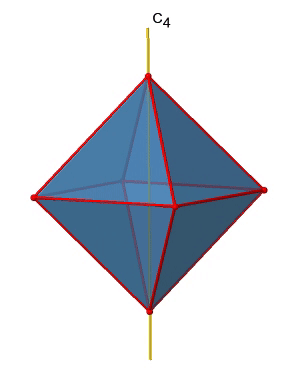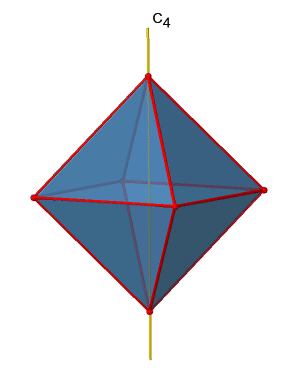
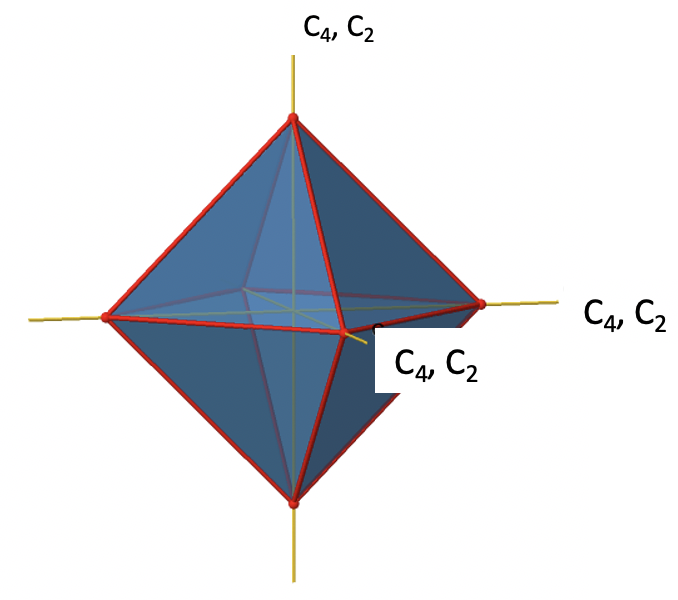
Ми бачимо, що є також осі C 2, де працюють осі C 4. Це пов'язано з тим, що обертання два рази навколо 90° таке ж, як обертання навколо 180°. Які операції симетрії пов'язані з цими елементами симетрії? Обертання чотири рази навколо 90° за допомогою осей C 4 створює ідентичність. Таким чином, ми повинні розглянути операції C 4 1, C 4 2, C 4 3 і C 4 4. Скільки з них унікальних? C 4 4 те ж саме, що і ідентичність, тому він не є унікальним, Крім того, C 4 2 ідентичний C 2 1, і, таким чином, C 4 2 також не є унікальним, і може бути виражений простішою операцією C 2 1. Це залишає C 4 1 і C 4 3 як єдині унікальні операції симетрії. Оскільки у нас є три осі C 4, є 2x3 = 6 C 4 операції, докладно є 3C 4 1 і три операції C 4 3. Крім того, існують три операції С 2 1, що належать трьом осям С 2 (рис. 2.2.20).
Крім того, є чотири осі С 3 (рис.2.2.21). Вони йдуть через центр двох протилежних трикутних граней восьмигранника.
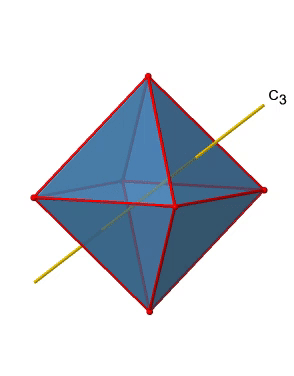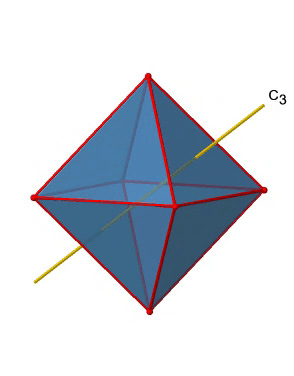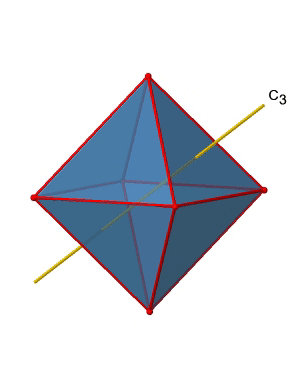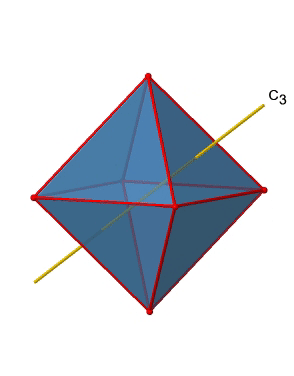
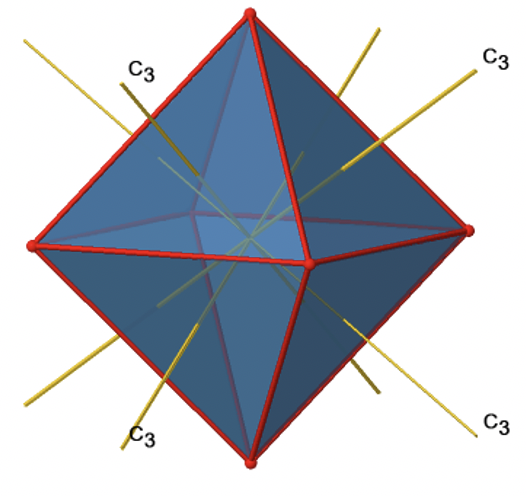
Ви бачите над однією віссю C 3, а з правого боку всі чотири ці осі. Як ми можемо зрозуміти, що існує чотири осі? Октаедр має загальні вісім трикутних граней, і кожна вісь C 3 проходить через дві протилежні грані, тому є осі 8/2 = 4 C 3. Кожна вісь C 3 має C 3 1 і C 3 2 як унікальні операції симетрії. C 3 3 - це те ж саме, що і ідентичність. Таким чином, в цілому у нас є 4x2 = 8 операцій, чотири з них C 3 1, і чотири з них C 3 2 (рис. 2.2.22).
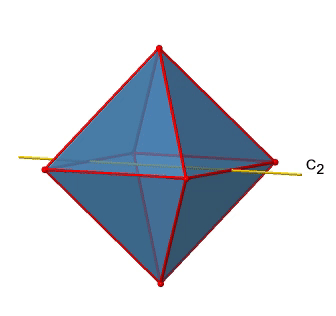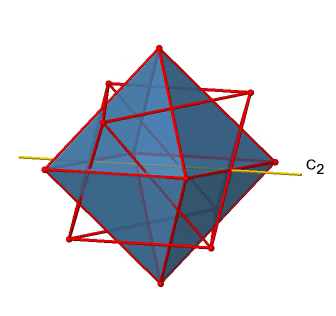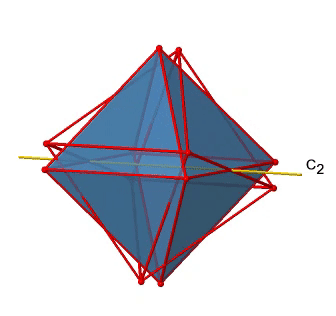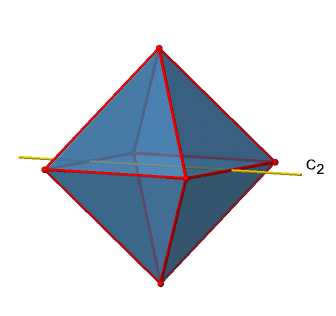
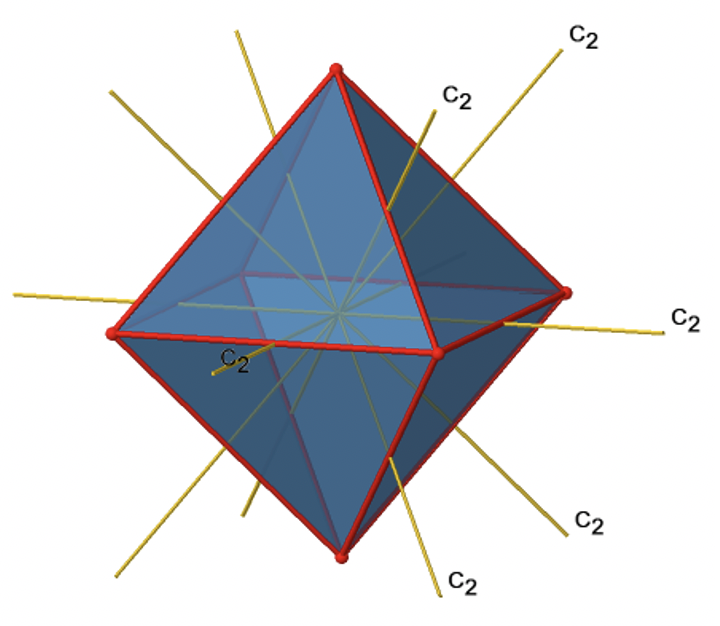
Крім осей С 2, які накладають осі C 4, є осі C 2 ', які йдуть через два протилежних краю октаедра (рис. 2.2.23). Скільки їх там? Октаедр має дванадцять ребер, і оскільки кожен C 2 'проходить через два ребра, повинні бути осі 12/2 = 6 C 2'. Ці осі мають простих чисел, оскільки вони не сполучені з осями C 2, які накладають осі C 4. Для кожної осі C 2 'є тільки C 2' 1 як унікальна операція симетрії, і тому є загальні 6 операцій симетрії C 2 '1 (рис. 2.2.24).
Подивимося на дзеркальні площини поруч (рис.2.2.25). Існують горизонтальні дзеркальні площини, які стоять перпендикулярно принциповим осям С 4. Ви можете побачити один з них нижче зліва.
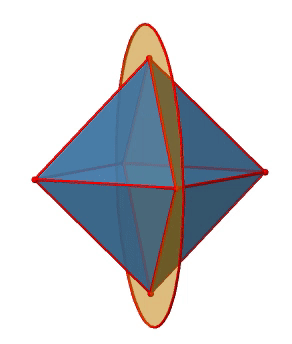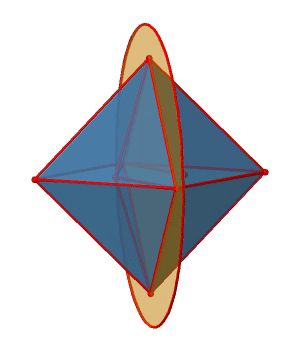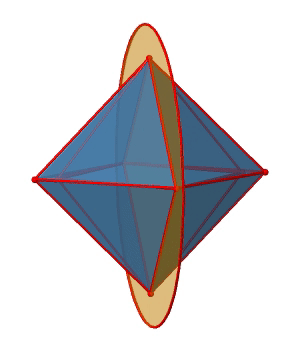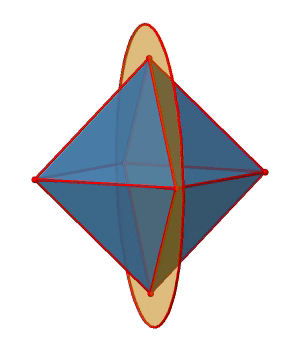
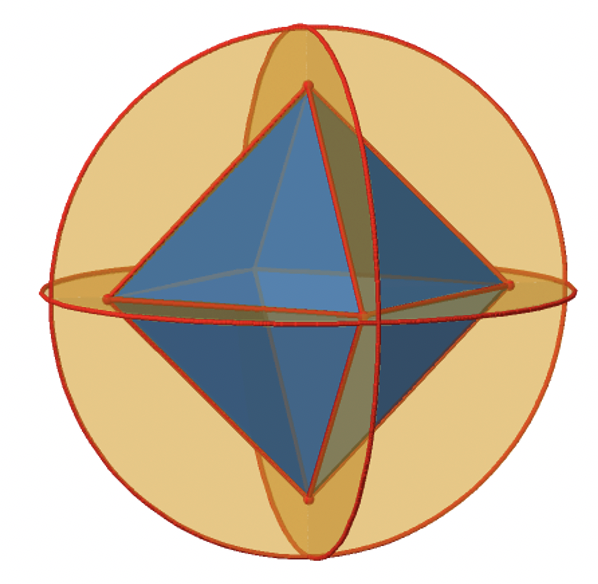
Зверніть увагу, що ця дзеркальна площина містить також дві осі, крім тієї, до якої вона стоїть перпендикулярно. Оскільки він містить дві основні осі C 4, він також має властивості вертикальної дзеркальної площини. Тим не менш, ми називаємо це горизонтальною дзеркальною площиною, оскільки вона стоїть перпендикулярно третьому C 4. Горизонтальні властивості перевершують вертикальні, так би мовити. Ви можете бачити, що одна дзеркальна площина містить чотири ребра октаедра. Оскільки є дванадцять країв, є 12/4 = 3 горизонтальні дзеркальні площини. Існує одна дзеркальна площина на головну вісь C 4. Існує три операції горизонтального відбиття, оскільки завжди існує лише одна операція відбиття на площину дзеркала (рис. 2.2.26).
Далі шукаємо вертикальні дзеркальні площини (рис.2.2.27). Внизу зліва зображена вертикальна дзеркальна площина.
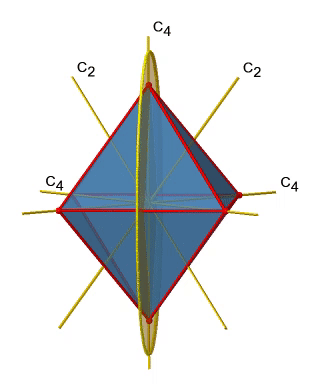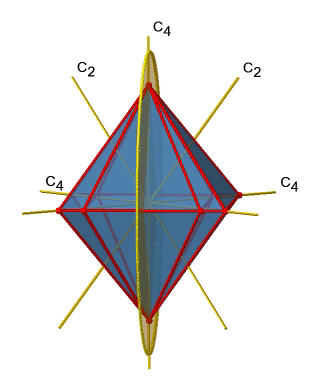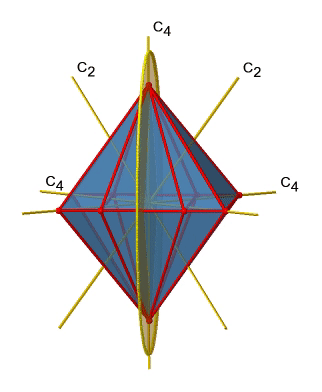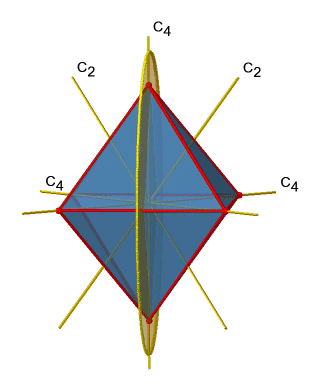
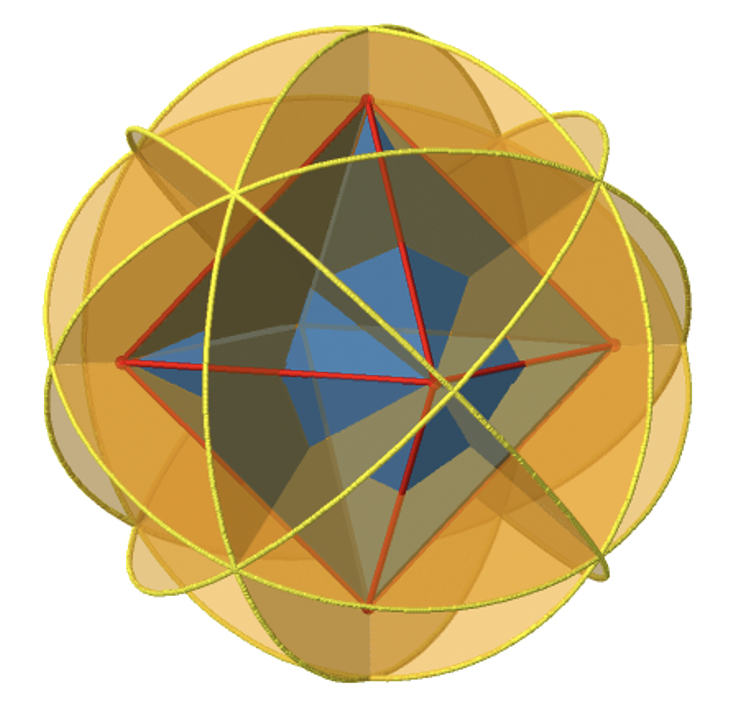
Ви можете бачити, що - на відміну від горизонтальних дзеркальних площин - він не містить жодних країв. Швидше, вона прорізає два протилежних краю. Ви можете бачити, що ця площина містить вісь C 4, але вона не стоїть перпендикулярно іншим двом осям C 4. Тому він має тільки властивості вертикальної дзеркальної площини. Однак ви можете бачити, що дзеркальна площина розсікає кут між двома осями C 2 ', які також зображені. Це робить вертикальні дзеркальні площини двогранними дзеркальними площинами, σ d. Скільки з них ми маємо? Як вже говорилося раніше, кожна дзеркальна площина прорізає два протилежних ребра. У октаедрі є дванадцять ребер, і, таким чином, є 12/2 = 6 двогранних дзеркальних площин. Ви можете побачити всі їх з правого боку рис.2.2.27. Кожна дзеркальна площина пов'язана з однією операцією відображення, тому існує шість операцій двогранного відображення (рис.2.2.28).
Далі ми можемо запитати, чи є точка група O h інверсійний центр? Так, в центрі восьмигранника є один (рис. 2.2.29)!
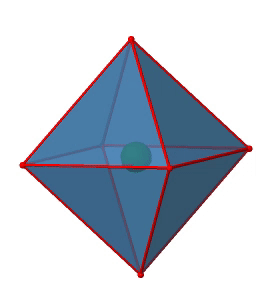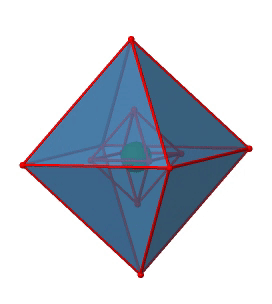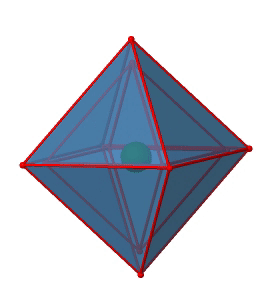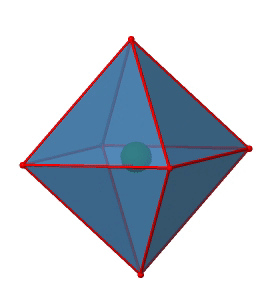
Малюнок 2.2.29 Центр інверсії восьмигранної точки групи O h (Атрибуція: symotter.org/gallery)
Кожну точку в октаедреоні можна переміщати через центр інверсії в іншу сторону, а отриманий октаедр буде накладати початковий. Завжди існує одна операція інверсії, пов'язана з центром інверсії (рис.2.2.30).
Далі шукаємо обертання-відбиття. Ви можете побачити операцію обертання-відбиття S 6 нижче (рис. 2.2.31, зліва).
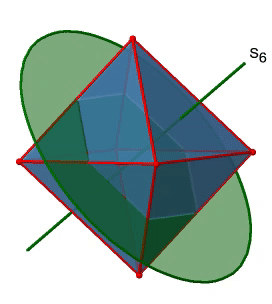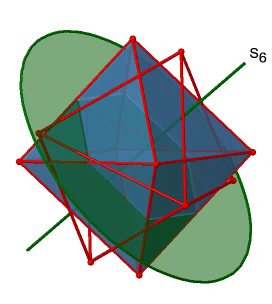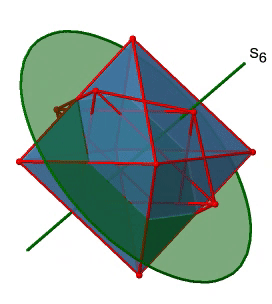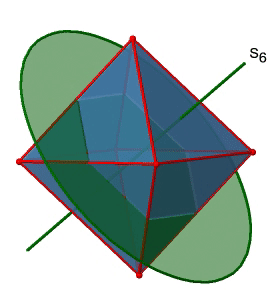
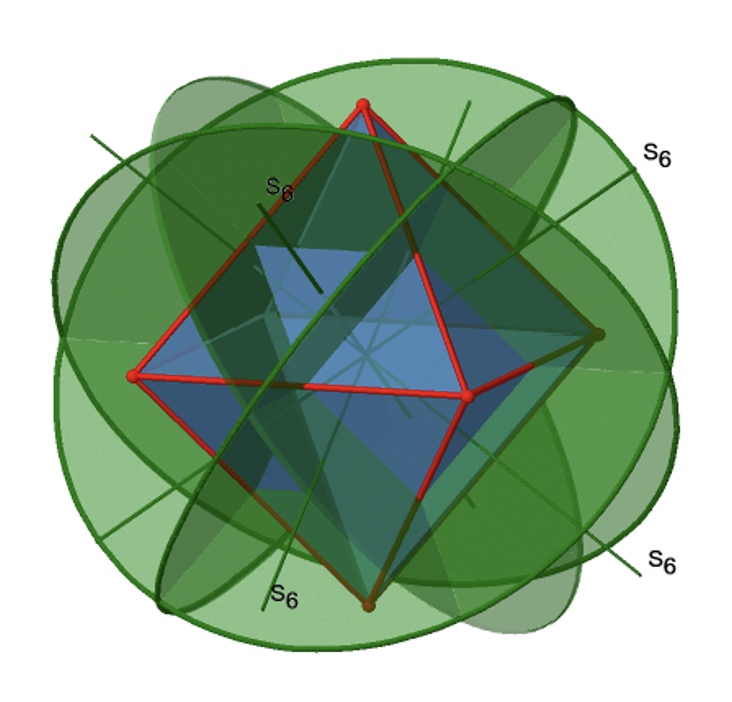
Неправильна вісь S 6 проходить через центри двох протилежних трикутних граней. Можна бачити, що лише обертання приблизно на 60° не змушує октаедр накладатися. Відбиття на площині, перпендикулярній неправильній осі, потрібно для досягнення суперпозиції. Загалом, обертання-відображення змінює положення двох протилежних трикутних граней. Скільки існує неправильних осей S 6? Оскільки кожен S 6 проходить через дві грані, а октаедр має 8 граней, має бути осі 8/2 = 4 S 4. Всі їх ви можете побачити вище (рис. 2.2.31, праворуч). Зверніть увагу, що вони знаходяться в тому ж положенні, що і осі 4C 3, про які ми говорили раніше. Скільки унікальних операцій пов'язано з ними? Для осі S 6 нам потрібно розглянути операції від S 6 1 до S 6 6. S 6 6 - це те саме, що ідентичність, тому вона не є унікальною. S 6 2 такий же, як C 3 1, оскільки обертання два рази навколо 60° таке ж, як обертання навколо 120°, а відображення двічі - це те саме, що не відображає взагалі. Аналогічно, S 6 4 такий же, як C 3 2. Обертання чотири рази на 60° таке ж, як обертання два рази на 120°, а відображення чотири рази - це те саме, що взагалі не відображає. Далі, S 6 3 - це те ж саме, що і інверсія. Після трьох обертань на 60° ми повернулися на 180°. Якщо ми розмірковуємо після цього, то це те саме, що операція S 2 1, яка є такою ж, як інверсія. Тому унікальними є тільки операції S 6 1 і S 6 5, всі інші операції можуть бути виражені більш простими операціями (рис.2.2.32).
Октаедр також має неправильні осі S 4, і ви можете побачити одну з них нижче (рис. 2.2.33, праворуч).
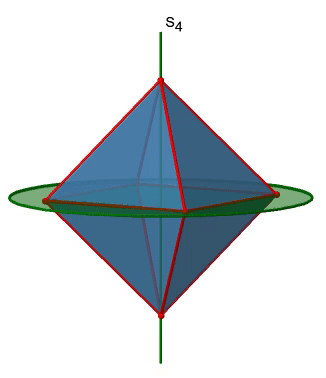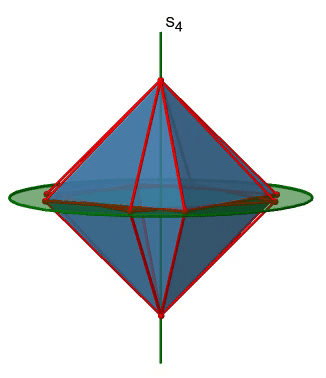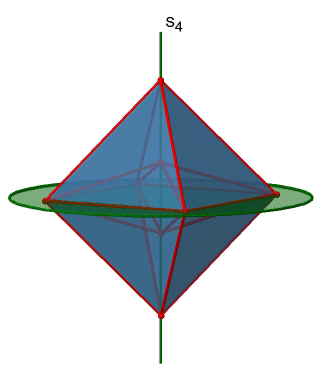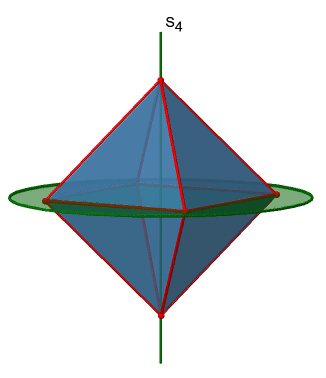
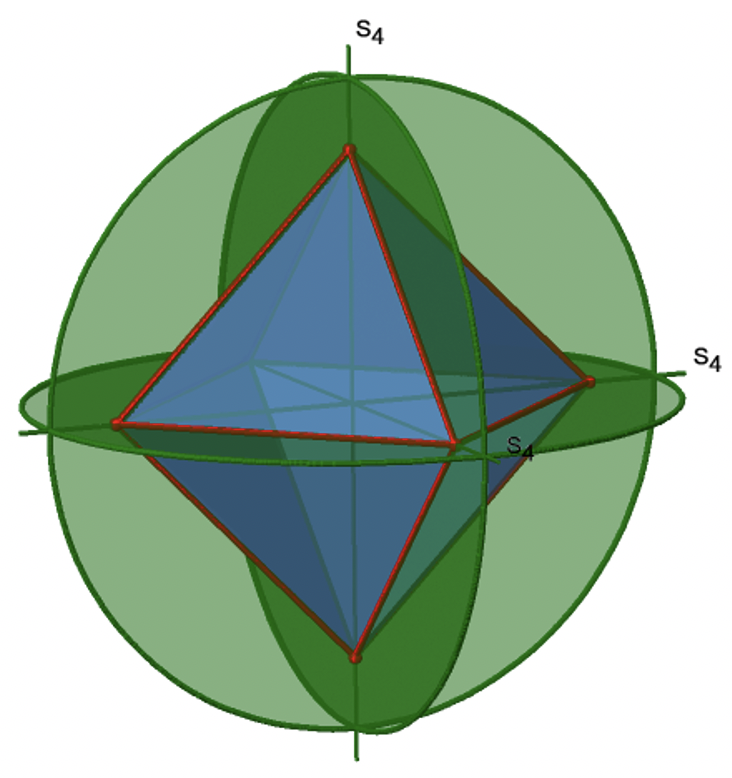
Вона проходить через два протилежних кута октаедра. Неправильна вісь S 4, здавалося б, робить те ж саме, що і вісь C 4, яка проходить через ті ж дві протилежні вершини, але насправді не робить. Під час обертання навколо 90° вже змушує октаедр накладатися з його початковою формою, виконуючи операцію відображення після обертання міняє положення двох вершин, і, як правило, всі точки октаедра над і нижче площини відповідно. Загалом S 4 переміщує точки всередині об'єкта по-різному порівняно з C 4, що робить його додатковим, унікальним елементом симетрії. Є загалом три неправильні осі S 4, оскільки октаедр має шість вершин, а одна S 4 проходить через дві вершини (рис. 2.2.34).
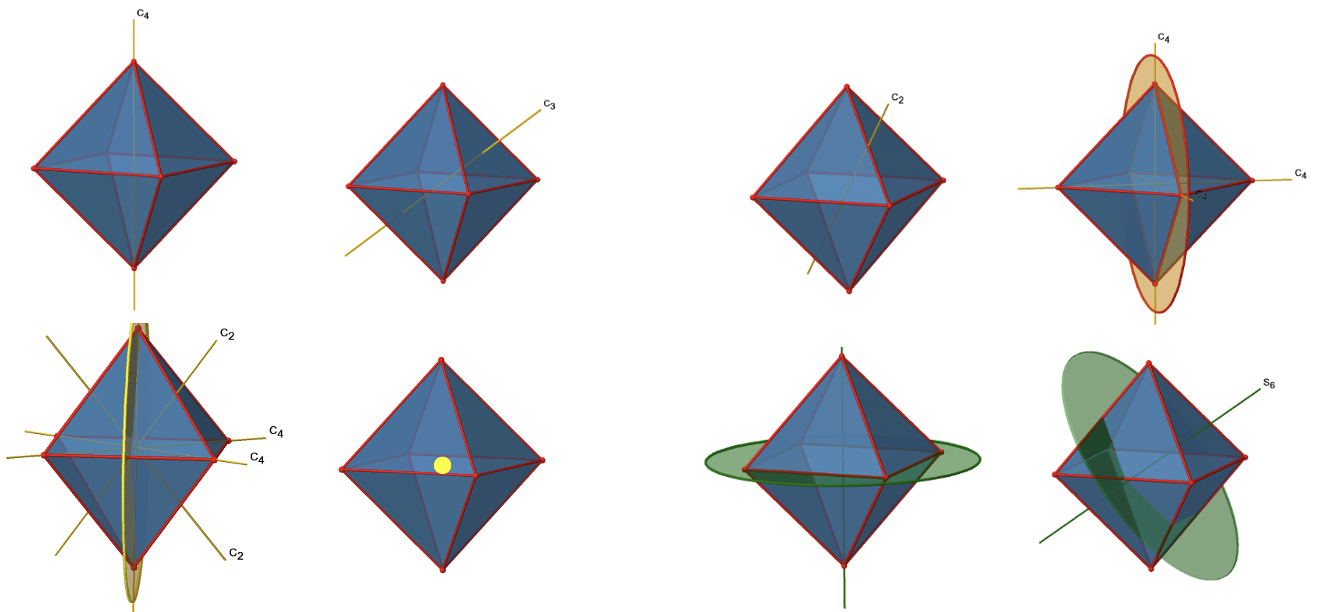
Ось огляд всіх елементів і операцій симетрії (рис. 2.2.35 і 2.2.36). Загалом, існує 48 різних унікальних операцій, які можна виконувати!
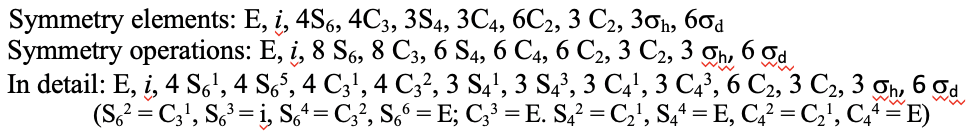
Як і точкова група T d, також точка група O h має обертальну підгрупу, названу О. має тотожність і ті ж власні обертання, що і точкова група O h, але ніяких інших операцій симетрії (рис.2.2.38). Прикладом може служити ядро кластера поліоксометалата, показане нижче (рис. 2.2.37). Поліоксометалати - кластерні аніони групи 5 і 6 елементів.
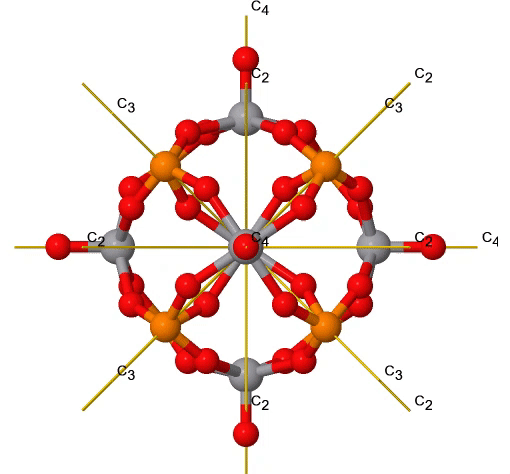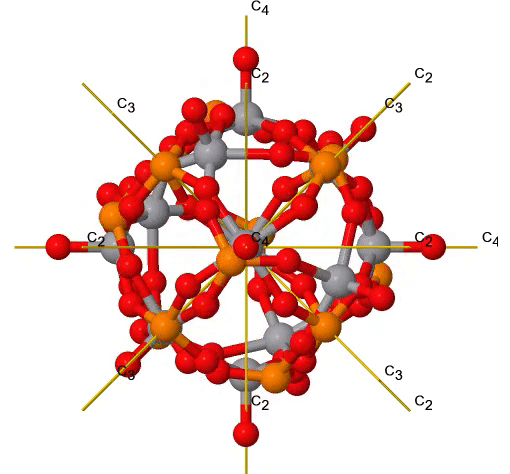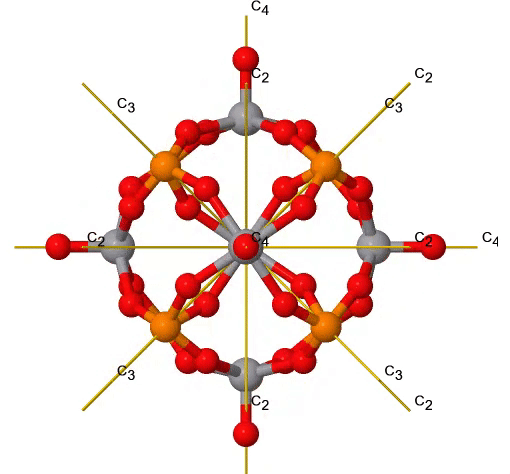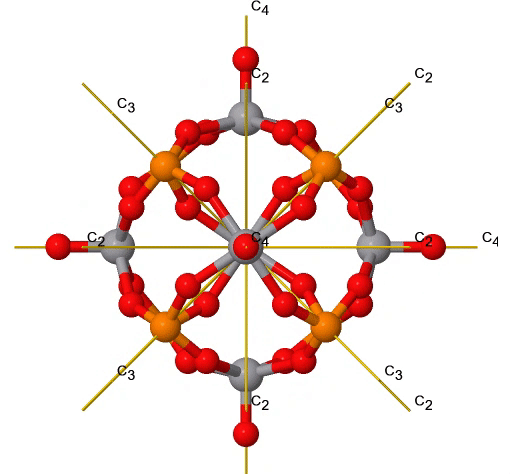
Малюнок 2.2.37 Правильні обертання в ядрі кластера поліоксометаліту V 6 P 8 O 24. Обертання C 3 анімоване. (Зазначення авторства: symotter.org/галерея)
Точкова група O, як правило, рідкісна.
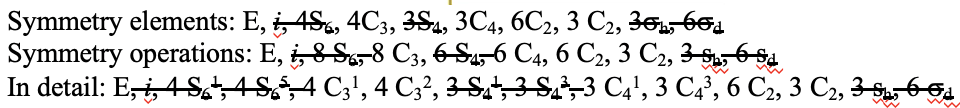
Ще однією групою точок високої симетрії є група точок T h. Його також можна вивести з групи точок O h. У цьому випадку операції S 4, C 4, C 2 'та σ d видаляються з восьмигранної симетрії. Прикладом може служити катіон гексапіридилзаліза (2+) (рис. 2.2.39).
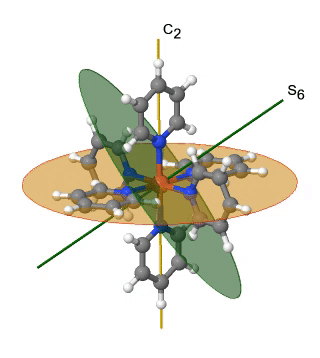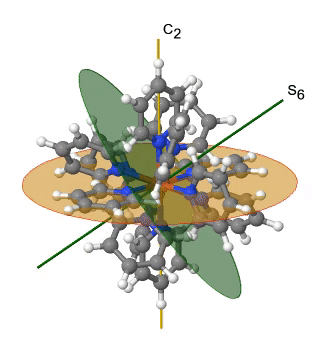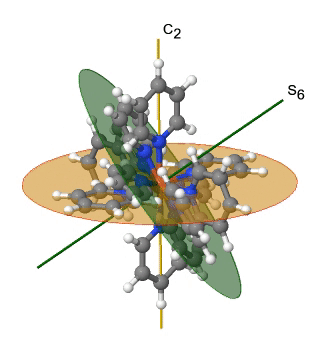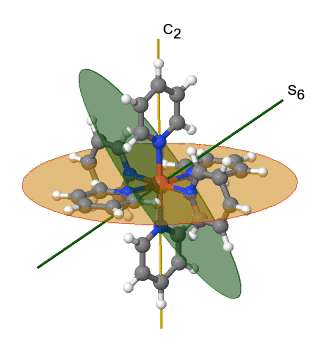
Малюнок 2.2.39 Катіон гексапіридильного заліза (2+) та його елементи симетрії S 6 і C 2. Операція S 6 анімована.
Ви можете бачити, що N-атоми піридил-лігандів оточують атоми Fe октаедрально, але симетрія зменшується від O h до T h через плоску форму піридил-лігандів. Зокрема симетрія С 4 зведена до С 2. Це зменшення симетрії призводить до усунення елементів S 4, C 2 'і σ d симетрії (рис. 2.2.40).
Група I h точка
Два залишилися платонічних твердих тіла, ікосаедр і додекаедр, належать обидва до ікосаедричної точкової групи I h. Це незважаючи на те, що вони зроблені з різних багатокутників (рис. 2.2.41).
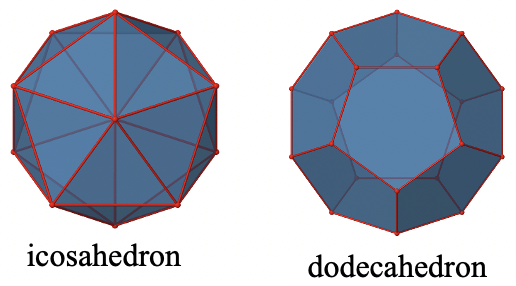
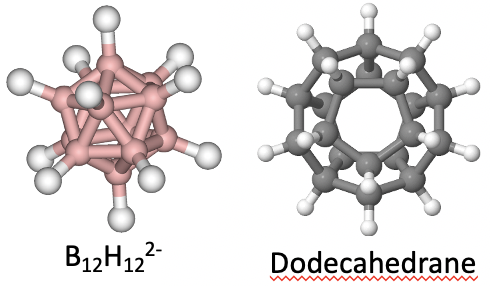
Оскільки вони належать до однієї групи точок, вони мають точно такі ж операції симетрії. Прикладом для молекули з ікосаедричною формою є молекулярний аніон B 12 H 12 2-. Прикладом для молекули з додекаедричною формою є додекаедран C 20 H 20.
Визначимо елементи симетрії і операції симетрії на прикладі ікосаедра. Ми також могли б використовувати додекаедр, і результати були б однаковими. Основними осями ікосаедра є осі С 5. Ви можете побачити одну з них, що проходить через центр петагону, що складається з п'яти трикутних граней внизу (рис. 2.2.43).
Малюнок 2.2.43 Одна з осей С 5 ікосаедра стоїть перпендикулярно паперовій площині, що проходить через центр п'ятикутника ікосаедра (Attribution: symotter.org/gallery)
Ви можете зрозуміти, що існує С 5, якщо врахувати, що існує п'ять трикутних граней, що роблять п'ятикутник. Вісь С 5 сидить в центрі п'ятикутника. Ми бачимо, що коли ми обертаємося навколо цієї осі C 5, то отриманий ікосаедр накладає початковий. Вісь С 5 проходить через дві протилежні вершини ікосаедра. Оскільки ізосаедр має 12 вершин, загалом має бути шість осей C 5. Всі їх ви можете побачити нижче (рис.2.2.44).
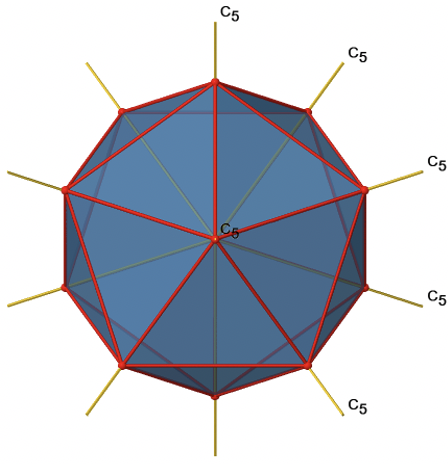
Існує чотири унікальні операції симетрії, пов'язані з однією віссю C 5, а саме C 5 1, C 5 2, C 5 3 і C 5 4. C 5 - це те ж саме, що і ідентичність. Оскільки існує шість осей C 5, існують загальні операції симетрії 6x4=24 C 5 (рис. 2.2.45).
Крім того, є осі С 3. Один з них показаний нижче, і можна помітити, що він проходить через центри двох протилежних трикутних граней (рис.2.2.46).
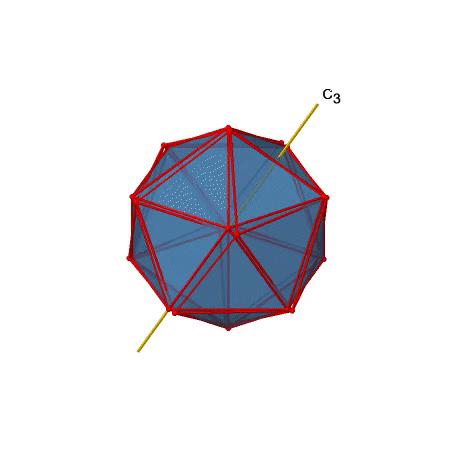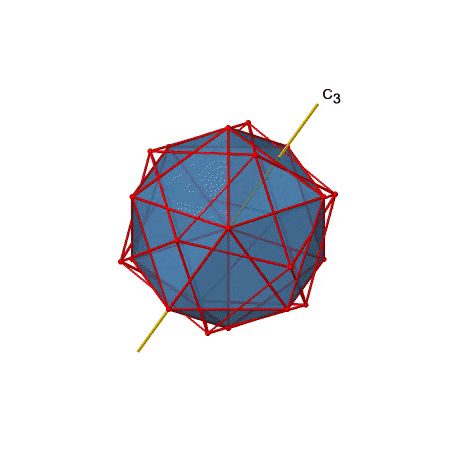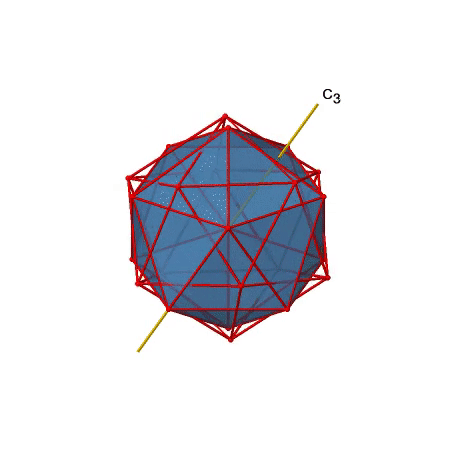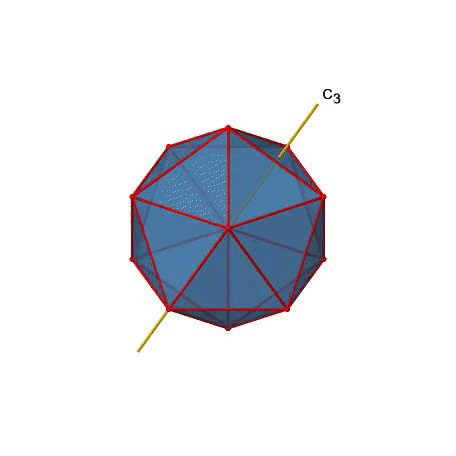
При обертанні на 120° атоми на трикутних гранях змінюють своє положення, а отриманий ікосаедр накладає початкове. Як говорить назва ікосаедра, загалом двадцять облич.
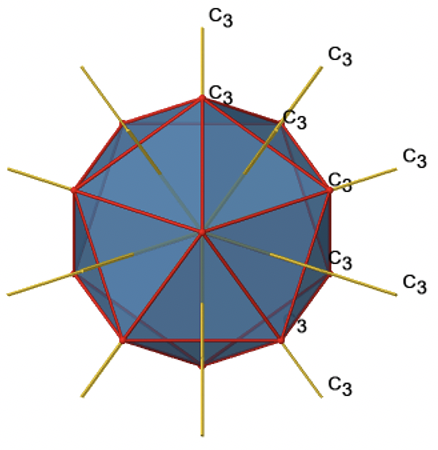
Оскільки одна С 3 проходить через дві протилежні осі, є загальні осі 20/2=10 С 3 (рис. 2.2.47). Кожна вісь С 3 пов'язана з двома операціями симетрії, а саме C 3 1 і C 3 2. Таким чином, існують загальні операції симетрії 10x2=20 C 3.
Існують також осі С 2 (рис. 2.2.49). Вони проходять через центри двох протилежних країв ікосаедра. Обертання навколо показаної осі C 2 змушує ікосаедр накладатися.
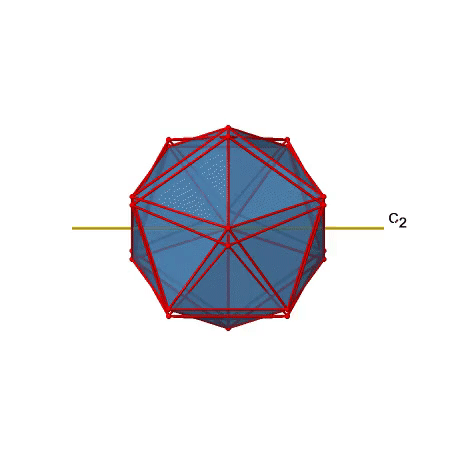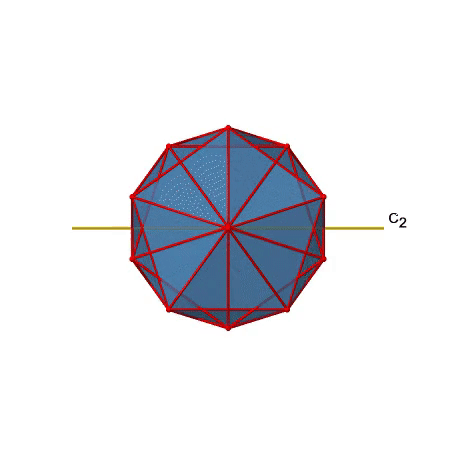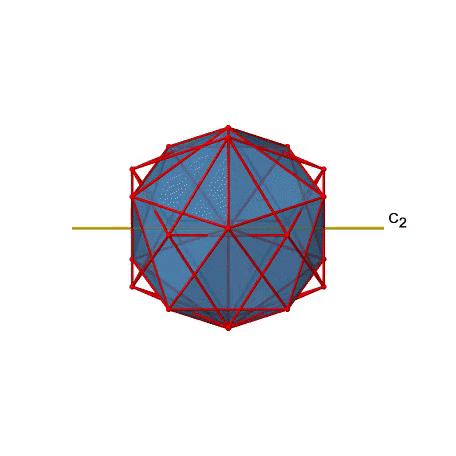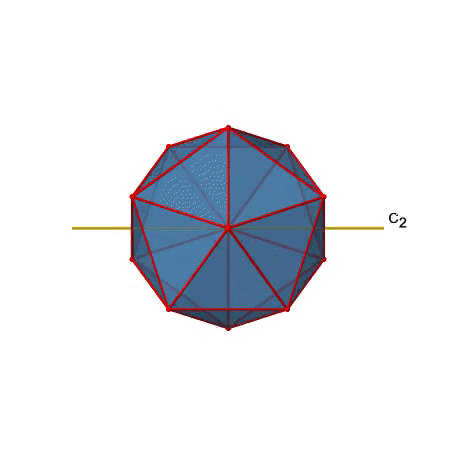
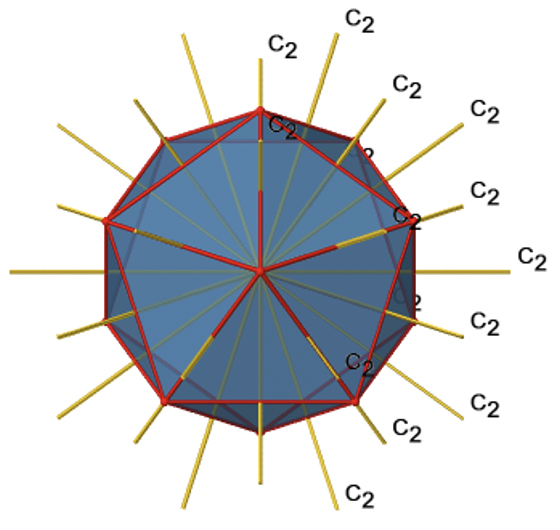
Ізосаедр має загальні 30 країв. Оскільки одна вісь C 2 проходить через центри двох протилежних країв, ми можемо зрозуміти, що є осі 30/2 = 15 C 2. Існує одна унікальна операція С 2 на вісь, і тому існує 15 операцій С 2 (рис.2.2.50).
Зараз ми знайшли всі правильні обертання. Давайте шукати дзеркальні площини, далі. Ви можете побачити дзеркальну площину внизу (рис. 2.2.51).
Малюнок 2.2.51 Дзеркальна площина в ікосаедричній точковій групі (Атрибуція: symotter.org/gallery)
Вона містить два протилежних краю. Він також перетинає два інших краю. Ікосаедр має загальні 30 країв, тому є 30/2=15 дзеркальних площин. Всі їх ви можете побачити нижче (рис. 2.2.52 і рис.2.2.53)).
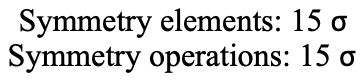
Ікосаедр також має центр інверсії в центрі ікосаедра (рис. 2.2.54 і рис.2.2.55)).
Малюнок 2.2.54 Центр інверсії в ікосаедрі (Зазначення авторства: symotter.org/gallery)
Коли ми виконуємо пов'язану, одну операцію симетрії, всі точки ізосаедра переміщаються через центр інверсії на іншу сторону.
Давайте тепер пошукаємо неправильні обертання. Неправильні осі обертання з найвищим порядком - осі S 10. Вони розташовуються в тому ж положенні, що і осі С 5, і проходять через два протилежних кута (рис.2.2.56).
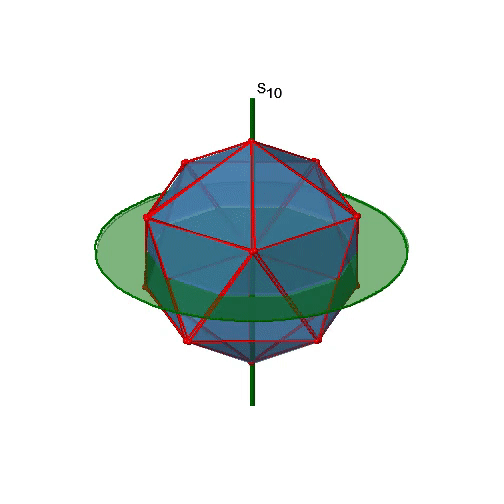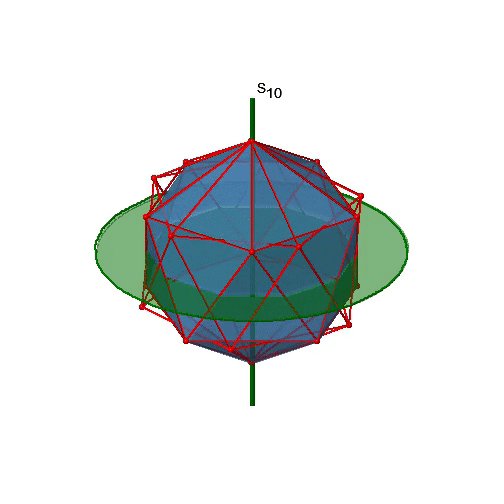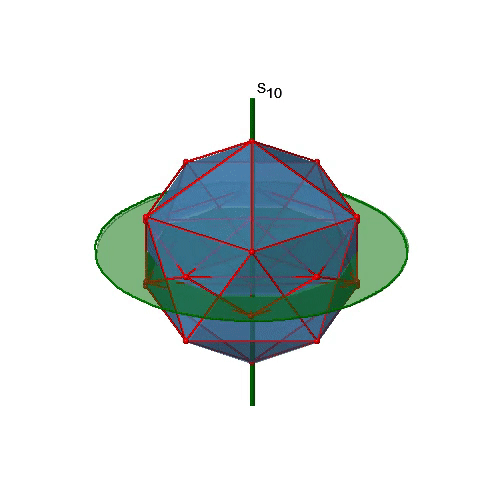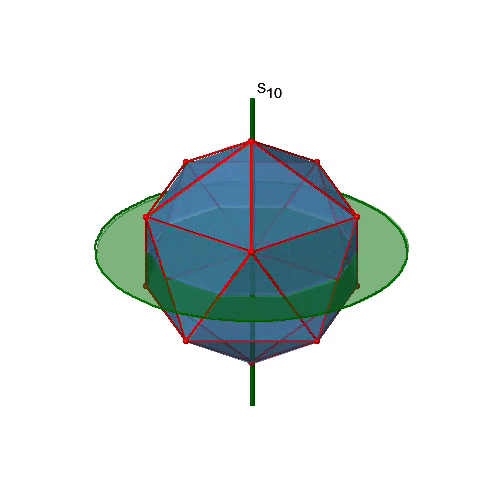
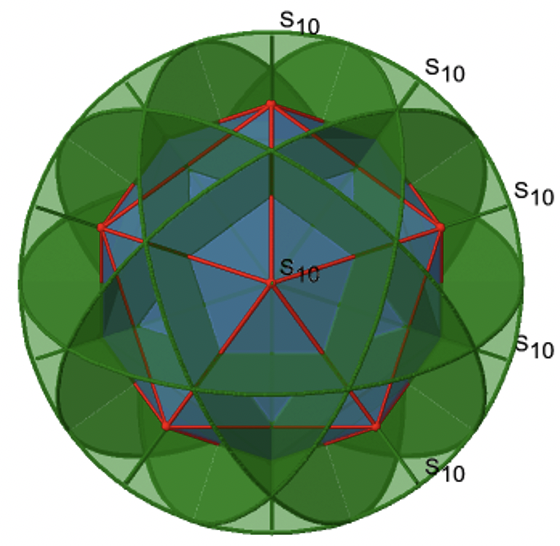
S 10 існує тому, що в ікосаедрі є пари співплощинних п'ятикутників, які орієнтовані в шаховому порядку відносно один одного. Обертання навколо 36° приводить один п'ятикутник у затемнене положення відносно іншого, але суперпозиція досягається лише після відображення на площині дзеркала перпендикулярно осі обертання. Оскільки одна S 10 проходить через дві протилежні вершини, а є 12 вершин, є 6 S 10 неправильних осей. Для кожної осі є чотири унікальні операції симетрії, S 10 1, S 10 3, S 10 7 і S 10 9. Отже, можливі загальні операції 4х6 = 24 (рис. 2.2.57).
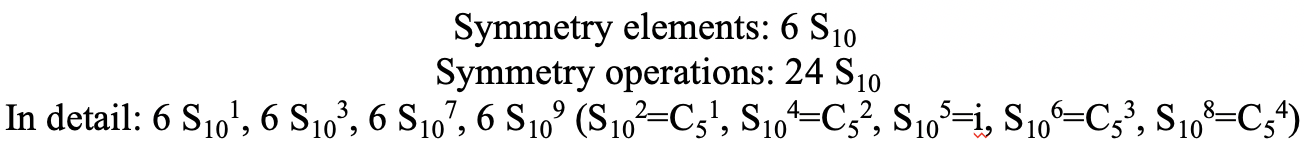
Чи є нижчим порядком неправильні осі обертання? Так, існують осі S 6, які проходять через центри двох протилежних трикутних граней (рис.2.2.58). Цей елемент симетрії існує тому, що дві трикутні грані знаходяться в шаховому порядку один до одного. Одне обертання приводить одну грань в затемнену орієнтацію щодо іншого, але відображення в дзеркальній площині, перпендикулярній осі, потрібно для досягнення суперпозиції. Осі S 6 знаходяться в тому ж місці, що і осі С 3.
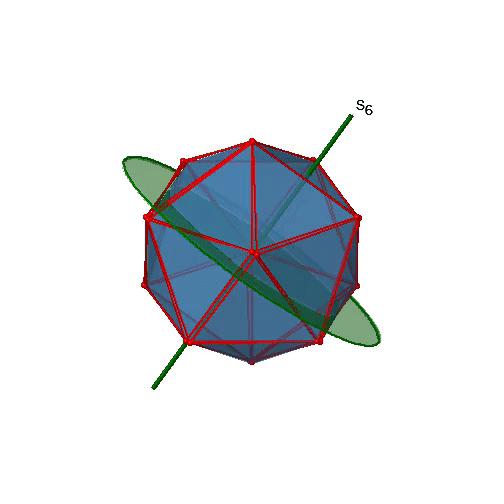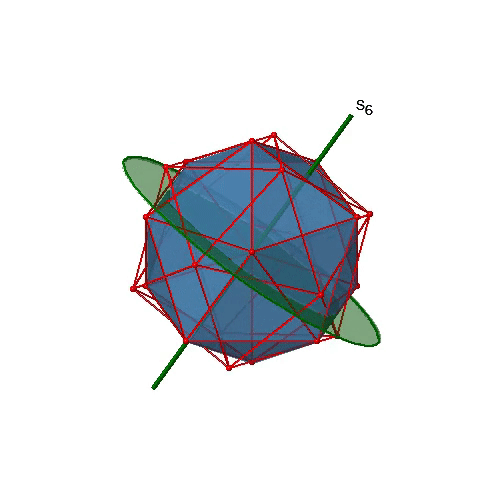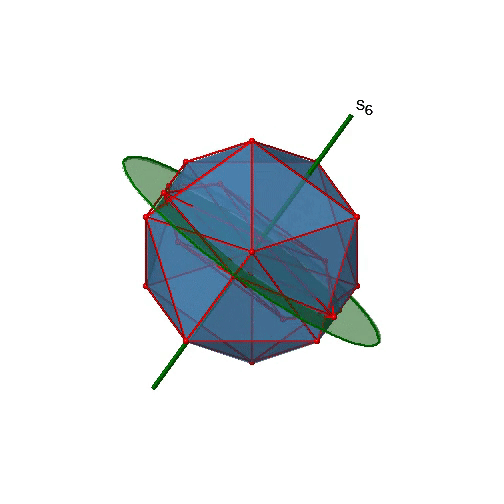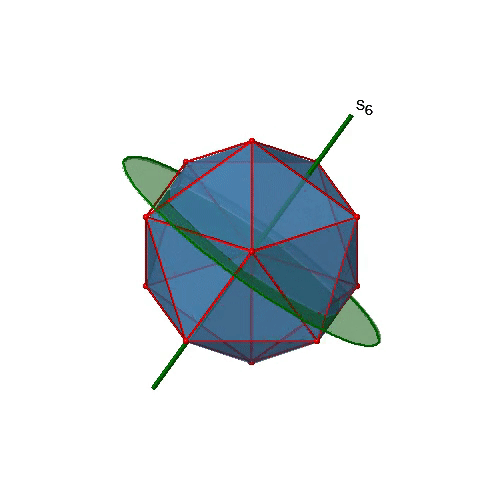
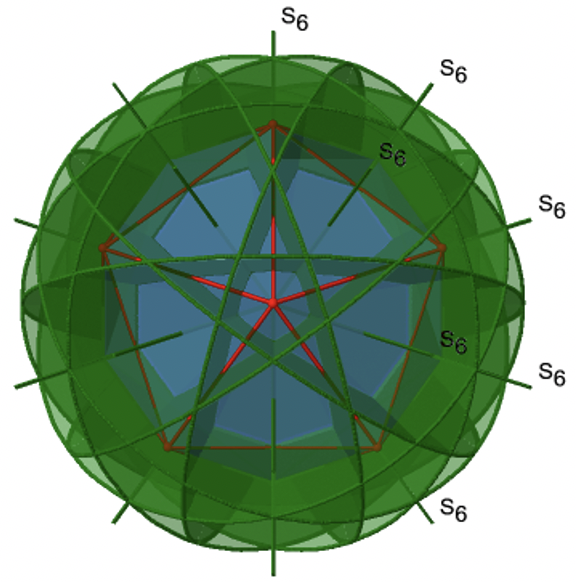
Є 10 осей S 6, оскільки є двадцять граней, а одна вісь проходить через дві протилежні грані. Тільки операції S 6 1 і S 6 5 є унікальними операціями S 6, всі інші можуть бути виражені більш простими операціями. Тому існують загальні 10 S 6 1 +10 S 6 5 = 20 S 6 операцій (рис.2.2.59).
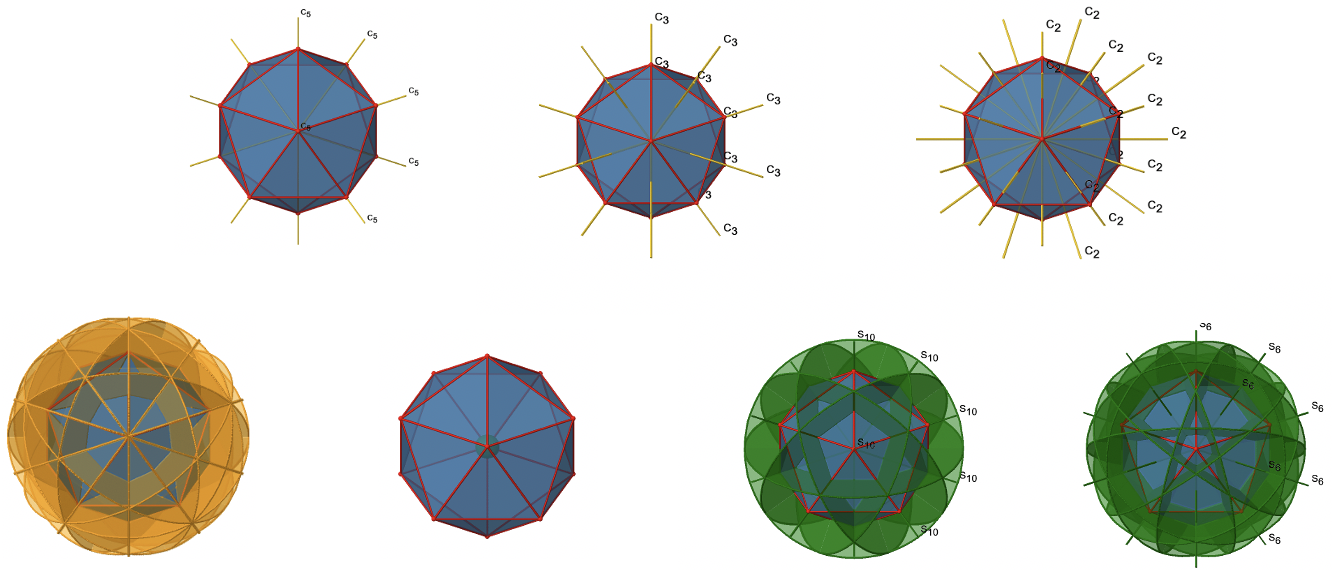
Тепер ми знайшли всі операції симетрії для симетрії I h. Всього виконано 120 операцій, що роблять точкову групу I h точковою групою з найвищою симетрією (рис. 2.2.60 і рис. 2.2.61).
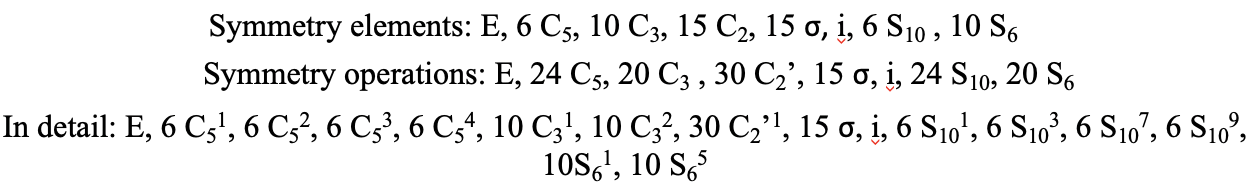
Також точкова група I h має обертальну підгрупу.
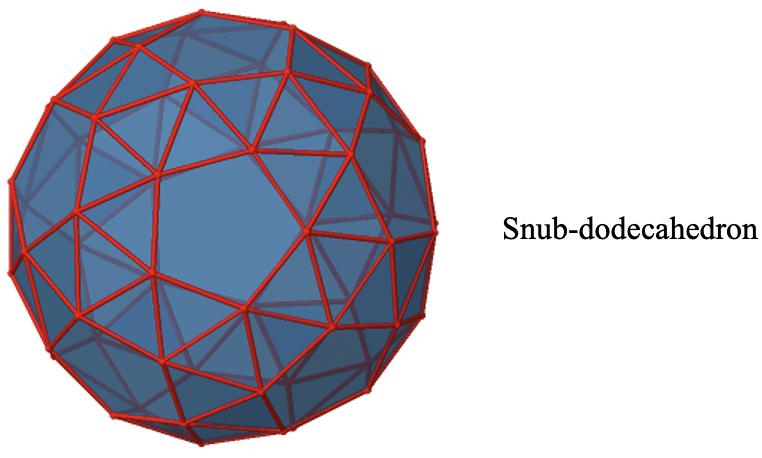
Називається він І. Прикладом об'єкта з такою симетрією є снуб-додекаедр (рис.2.2.62). Він має тотожність, і всі правильні операції обертання точкової групи O h, але виключені інверсія, обертання-відбиття і дзеркальні площини (рис. 2.2.63).
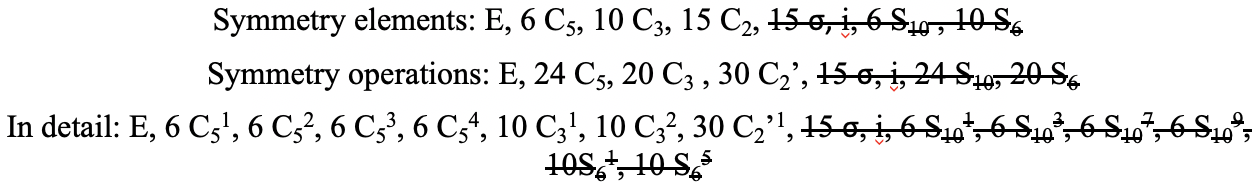
Циклічні групи точок
Після обговорення груп точок високої та низької симетрії, давайте далі розглянемо циклічні групи точок. Вони мають властивість, що вони мають тільки одну належну n-кратну вісь обертання, але ніяких інших належних осей. У найпростішому випадку вони не мають ніякого додаткового елемента симетрії, такого як дзеркальні площини або обертання-відбиття. Ці групи точок позначаються C n, де n - порядок відповідної осі. Прикладом може служити молекула пероксиду водню H 2 O 2 (рис.2.2.64).
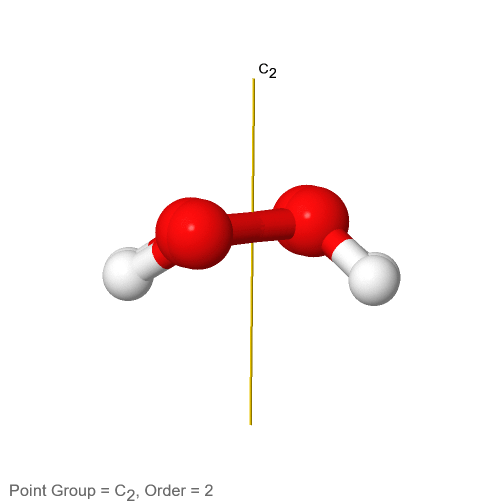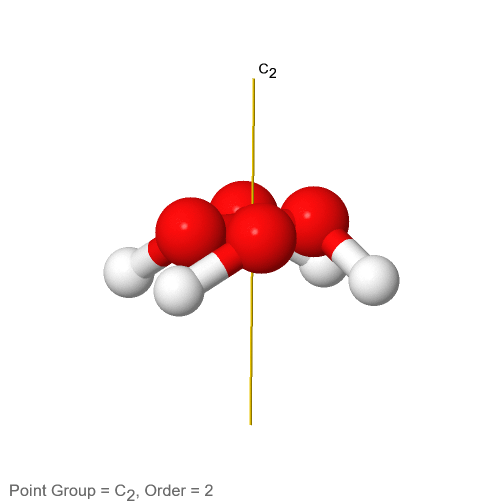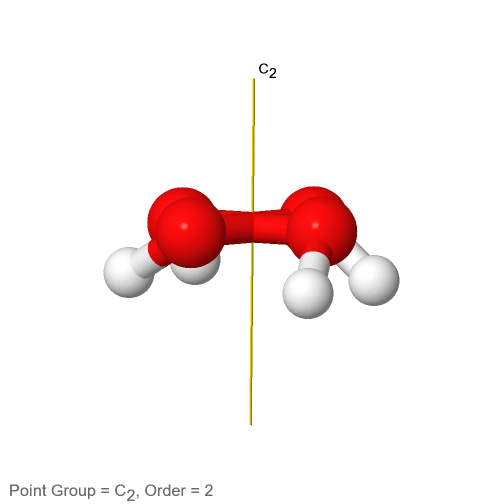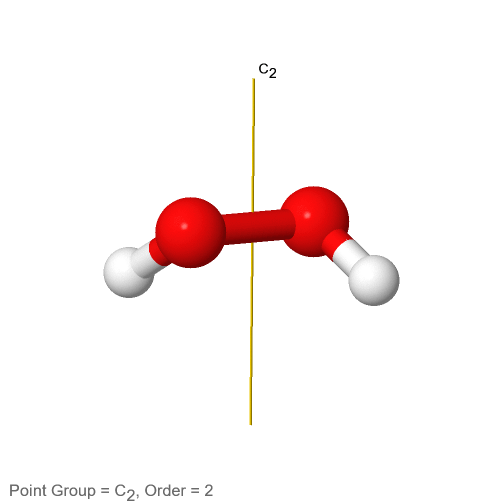
Малюнок 2.2.64 Вісь обертання пероксиду водню С 2
Має так звану дахову конструкцію завдяки своїй неплощинности. Один атом водню вказує на нас, а інший вказує на нас. Така структура обумовлена двома електрон-одинокими парами на кожному sp 3 -гібридизованому атомі кисню. Ці електрон-одинокі пари споживають дещо більше місця, ніж атоми Н, і між парами електронів одиноких електронів відбувається електростатичне відштовхування. Тому електронні одинокі пари при різних атомах кисню намагаються досягти найбільшої відстані один від одного. Це змушує Н-атоми вийти з площини, приводячи до покрівлі пероксиду водню. Оскільки молекула H 2 O 2 не планарна, вона має лише одну вісь C 2, але жоден інший елемент симетрії, крім ідентичності. Вісь С 2 проходить через центр зв'язку О-О. Виконання операції C 2 міняє як атоми O, так і H.
Визначення: Циклічні групи C n
Циклічні групи мають одну ротаційну аксіпірамідальну групу.
Іншим класом груп є пірамідальні групи, що позначаються C nv. Вони мають n вертикальних дзеркальних площин, що містять головну вісь C n на додаток до головної осі C n. Як правило, молекули, що належать до пірамідних груп, походять від n-гональної піраміди. N-гональна піраміда має n-гональний багатокутник як основу, яка обмежена (рис. 2.2.66).
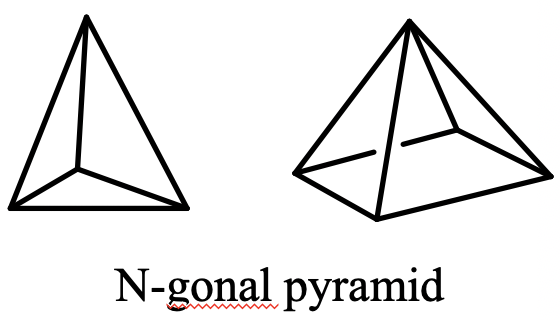
Наприклад, трикутна піраміда має трикутну основу, яка обмежується, чотирикутна піраміда має квадрат, який обмежений тощо. Правильна вісь, пов'язана з певною пірамідою, має порядок n і проходить через верхівку піраміди і центр багатокутника. Прикладом молекули з тригональної пірамідальної формою є NH 3 (рис. 2.2.67).
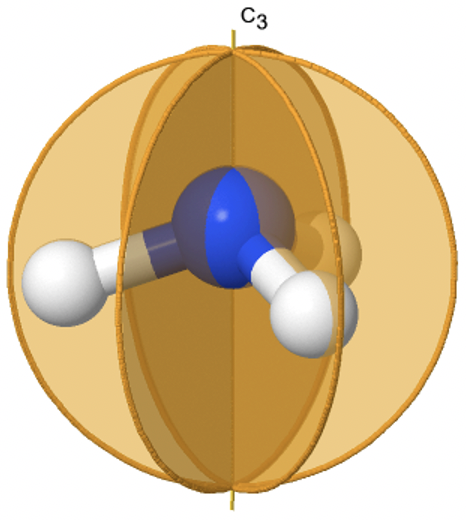
Три атоми Н утворюють трикутну основу піраміди, яка обмежується атомом N. Молекула NH 3 відноситься до точкової групи C 3v. Вісь C 3 проходить через атом N, який є кінчиком піраміди, і центром трикутника, визначеного атомами H. Є три вертикальні дзеркальні площини, які містять вісь С 3. Кожен з них проходить через N-H зв'язок (рис.2.2.68).
Визначення: Пірамідальні групи C nv
Пірамідальні групи мають n вертикальних площин на додаток до головної осі C n.
Лінійна група C ∞ v
Спеціальним n-гональним багатокутником є конус. Конус може бути задуманий як n-кутова піраміда з нескінченною кількістю n кутів біля основи (рис.2.2.69).
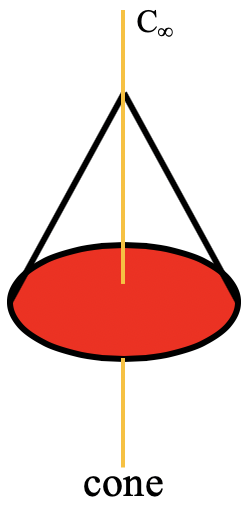
При цьому порядок осі обертання, яка проходить через кінчик конуса і центр круглої основи, нескінченний. Це також означає, що існує нескінченна кількість вертикальних дзеркальних площин, які містять вісь C ∞ (рис.2.2.71). Точкова група, що описує симетрію конуса, називається лінійною точковою групою C ∞ v. До цієї групи точок належать полярні, лінійні молекули, такі як CO, HF, N 2 O та HCN. Ви можете побачити молекулу HCN з її віссю C ∞ і її нескінченною кількістю вертикальних дзеркальних площин нижче (рис.2.2.70).
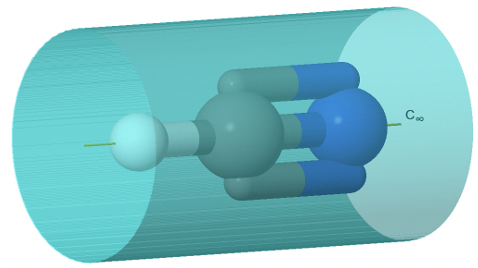
Нескінченна кількість дзеркальних площин, показаних синім кольором, утворюють циліндр, який оточує молекулу.
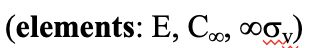
Визначення: Лінійна група С
Лінійна група C ∞ v має нескінченну кількість вертикальних дзеркальних площин, що містять вісь C ∞
Групи рефлексії
Якщо додати горизонтальну площину дзеркала замість n вертикальних площин дзеркала до належної осі обертання C n, ми прийдемо до групи точок відображення типу C nh. Наявність горизонтальних дзеркальних площин також породжує неправильну вісь порядку n Це пов'язано з тим, що коли можна обертати і відображати перпендикулярно осям обертання незалежно, то також можна робити це в поєднанні. Прикладом молекули, що належить до групи відображення, є транс-дифтордіазол N 2 F 2 (рис.2.2.72).
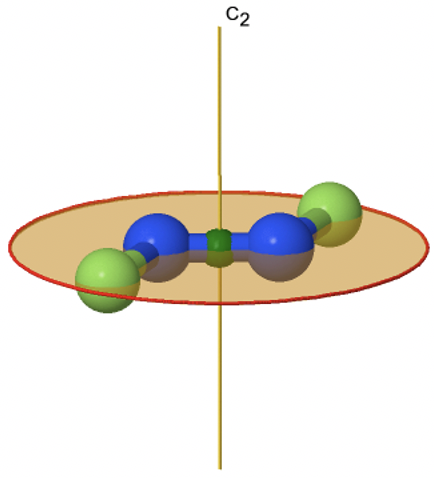
Це плоска молекула з віссю С 2, що проходить через середину подвійного зв'язку N-N і стоїть перпендикулярно площині молекули. Горизонтальна дзеркальна площина стоїть перпендикулярно осі С 2, і знаходиться в межах площини молекули. Існує додатковий інверсійний центр, оскільки повинен існувати S 2, який є таким же, як центр інверсії. Центр інверсії знаходиться в середині N-N зв'язків. В цілому молекула має симетрію C 2h.
Визначення: Група відображення C nh
Група відбиття має горизонтальну площину, перпендикулярну головній осі C n.
двогранні групи
Двогранні групи - це точкові групи, які мають n додаткових осей С 2, які стоять перпендикулярно головній осі порядку n. якщо інших елементів симетрії немає, то точкова група має тип D n.
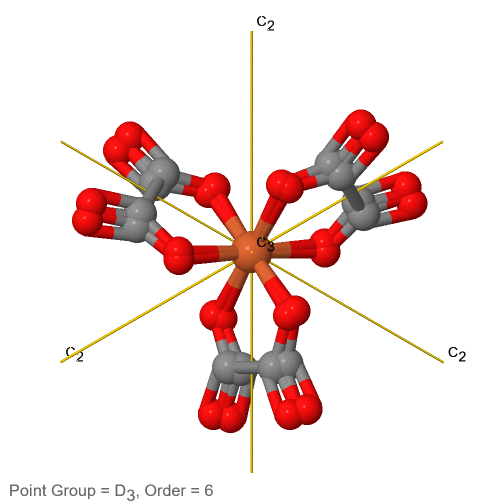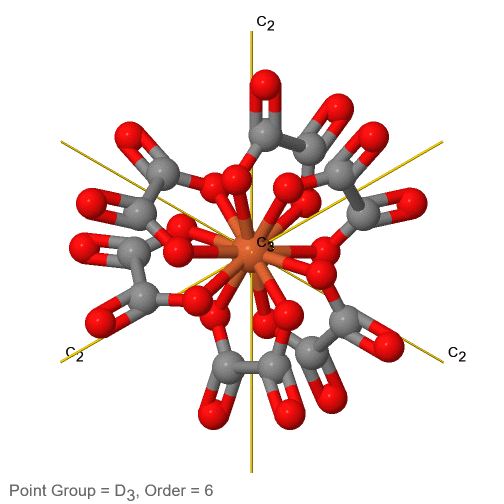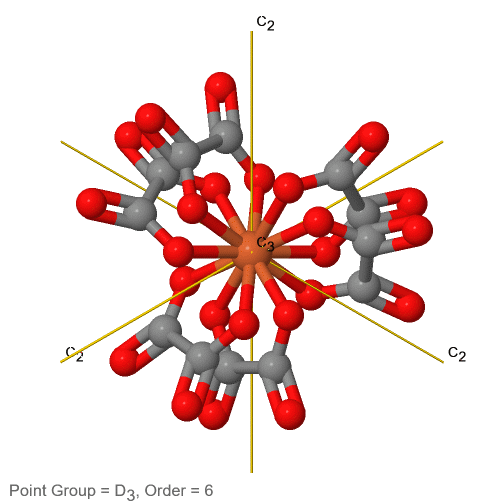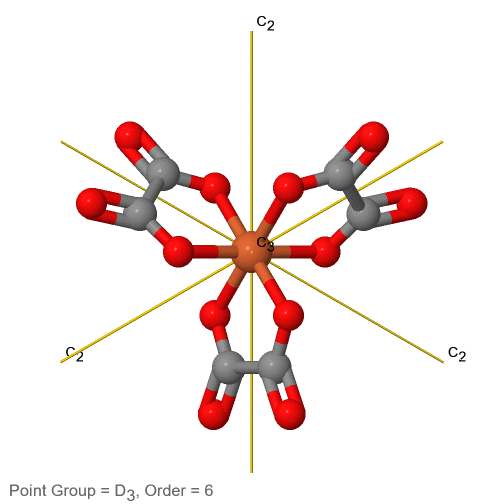3_C3.gif)
Малюнок 2.2.74 Трис-оксолато феррат (3-) іон та його елементи симетрії
Наприклад, в точковій групі D 3 є головна вісь С 3, і три додаткові осі С 2, але іншого елемента симетрії немає (рис.2.2.75). До цієї точкової групи належить іон трис-оксолато феррат (3-) (рис. 2.2.75). Ви можете бачити, що вісь С 3 стоїть перпендикулярно паперовій площині, а в паперовій площині є три осі С 2.
Визначення: Двогранні групи D n
У точковій групі типу D n є головна вісь порядку n, n осі C 2, але інших елементів симетрії немає.
Якщо до осі C n додати горизонтальну площину дзеркала, а осі n C 2 приходимо до призматичних точкових груп D nh (рис. 2.2.76). Додавання горизонтальної дзеркальної площини створює додаткові елементи симетрії, а саме S n та n вертикальних дзеркальних площин.
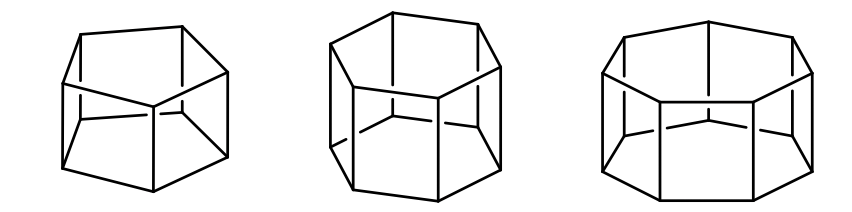
Як правило, молекули, що належать до цієї точкової групи, походять від n-гональних призм. Порядок головної осі такий же, як і кількість кутів багатокутників, з яких складається призма.
Визначення: Призматичні групи D nh
У призматичних точкових групах є горизонтальна дзеркальна площина, перпендикулярна головній осі C n. Є також n осей С 2.
Прикладом для молекули, що належить до призматичної точкової групи, є ПФ 5 (рис.2.2.77).
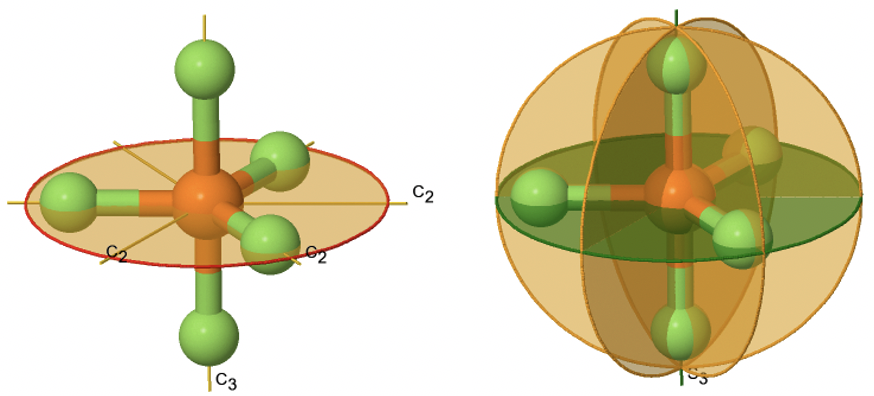
Має трикутну біпірамідальну форму. Вісь C 3 проходить через осьові атоми F молекули, а три осі C 2 проходять через три екваторіальних атома F. Горизонтальна дзеркальна площина стоїть перпендикулярно головній осі С 3 і розташовується в межах екваторіальної площини молекули. Крім того, існують вертикальні дзеркальні площини, які містять вісь С 3, і проходять через три екваторіальних P-F зв'язку. Існує також вісь S 3, яка накладає вісь C 3. У сумі:
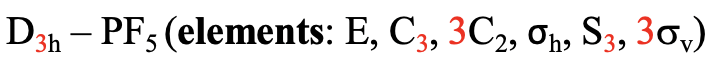
Окремим випадком групи D nh є лінійна група D ∞ h. Об'єкт, який має таку симетрію, - циліндр. Циліндр можна задумати як призму з нескінченною кількістю вершин. Таким чином, головна вісь, яка проходить через циліндр, має нескінченний порядок. Через нескінченний порядок головної осі існує нескінченна кількість осей C 2, які стоять перпендикулярно головній осі. Ви можете побачити один такий С 2, що йде хоч циліндр (рис 2.2.79).
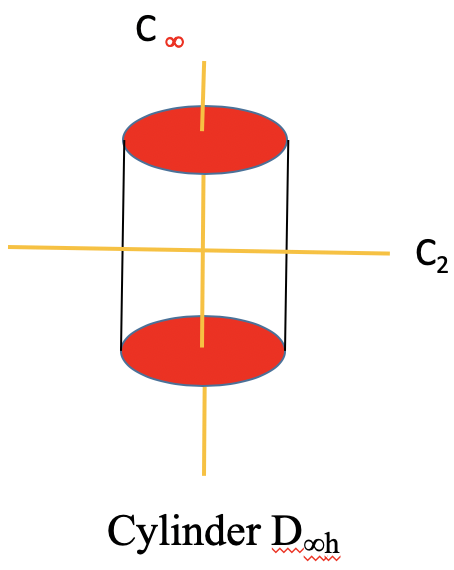
Існує тепер і неправильна вісь нескінченного порядку, а також нескінченна кількість вертикальних дзеркальних площин. Неполярні лінійні молекули, такі як H 2, CO 2 та ацетилен C 2 H 2, належать до точкової групи D ∞ h. Нижче ви можете побачити вісь C ∞, що проходить через молекулу CO 2 (рис. 2.2.80).
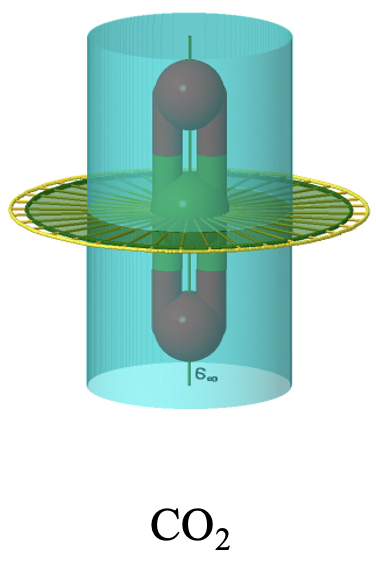
Ви можете побачити нескінченну кількість вертикальних дзеркальних площин у вигляді синього циліндра. Нескінченне число осей С 2 показано жовтими лініями, що йдуть навколо молекули. У сумі:
Визначення: Лінійна група D ooh
У точковій групі D ∞ є нескінченне число n осей C 2 на додаток до головної осі нескінченного порядку, нескінченна кількість вертикальних дзеркальних площин і одна горизонтальна дзеркальна площина.
Якщо ми додамо n вертикальних дзеркальних площин до головної осі і п осей C 2, ми прийдемо до групи точок D nd. Вертикальні дзеркальні площини є двогранними дзеркальними площинами, оскільки вони бісекціонують кут між осями C 2. Прикладом може служити молекула етану в шаховому порядку конформації, яка має симетрію D 3d (рис. 2.2.82).
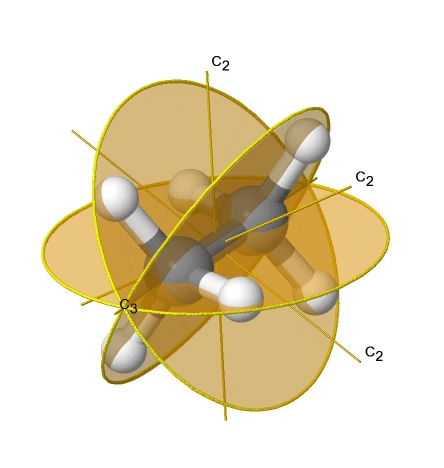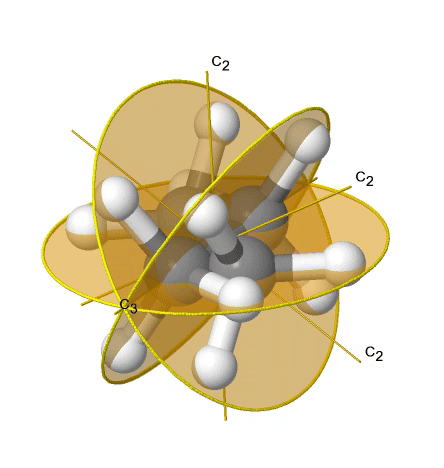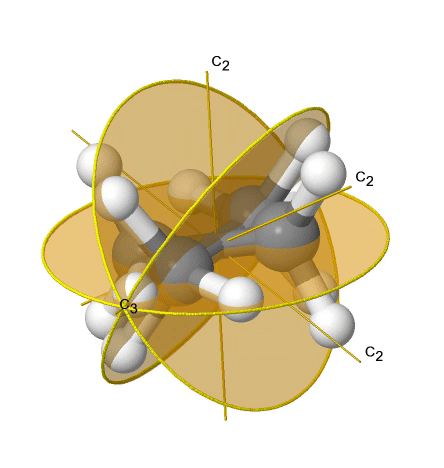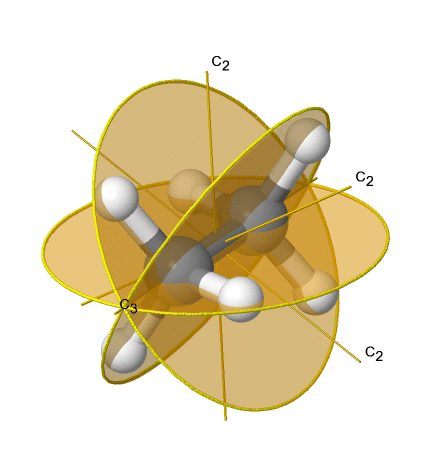
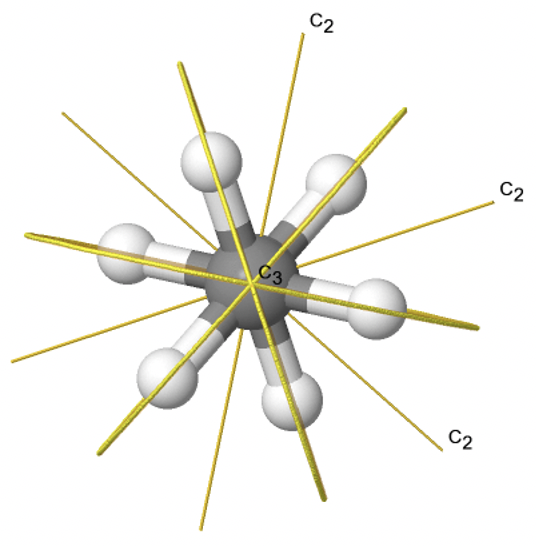
Вісь С 3 йде уздовж зв'язку С-С, а осі 3С 2 проходять через середину вуглецево-вуглецевого зв'язку, і розсікають кут між двома воднями і одним атомом вуглецю. Три двогранні дзеркальні площини проходять через C-H зв'язки. Крім того, молекула етану має вісь S 6, і центр інверсії. У сумі:
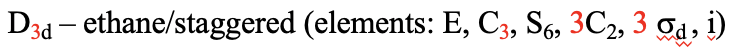
Визначення: D nd
У цьому типі групи точок є n двогранних дзеркальних площин, які містять C n і бісекційні кут між сусідніми осями C 2.
Неправильні групи обертальних точок
Останній клас груп точок, які слід обговорювати, - це неправильні групи точок обертання. Єдині мають одну правильну вісь обертання, і неправильну вісь обертання, яка має в два рази порядок правильної осі обертання (рис.2.2.85). Залежно від порядку належних та неправильних осей може бути присутнім інверсійний центр. Приклад молекули тетраметилциклоокта-тетраену (рис. 2.2.84).
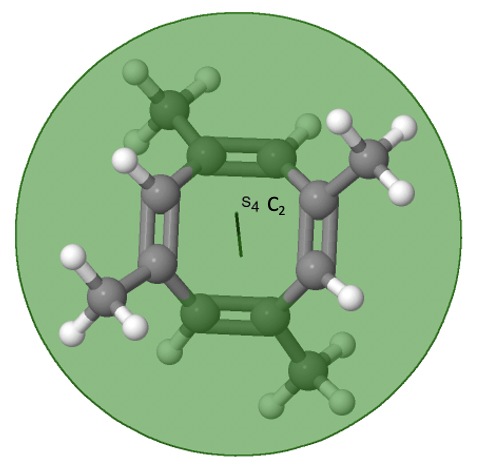
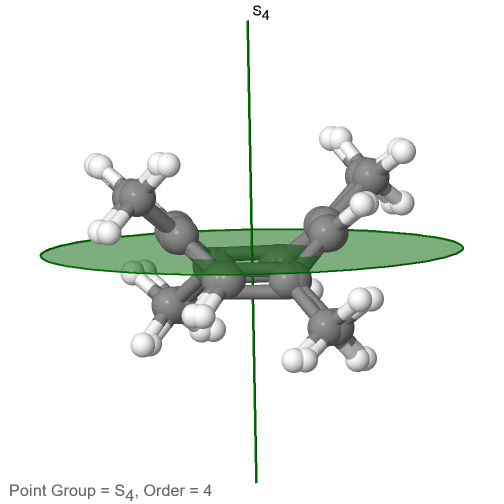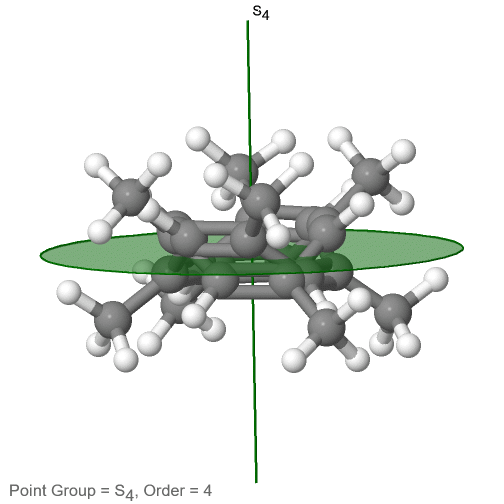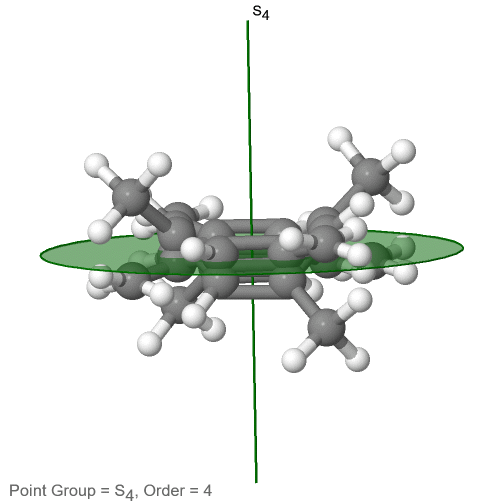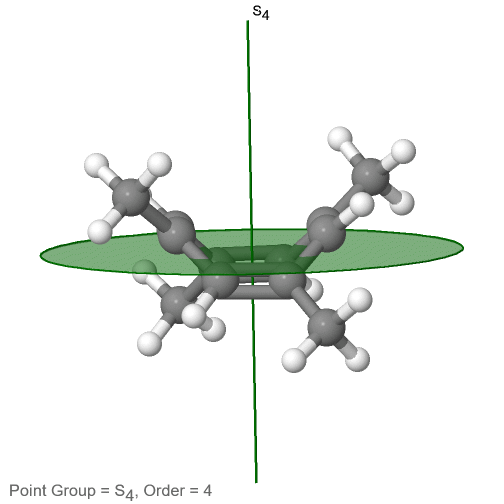
Малюнок 2.2.84 Осі S 4 та C 2 тетраметилциклоокта-тетраену
Він має вісь S 4 та C 2 як єдині елементи симетрії, крім ідентичності. Обертання лише на 90° не накладає молекулу, оскільки дві подвійні зв'язки C-C лежать над площиною, а дві - під площиною. Крім того, дві протилежні метильні групи лежать вище і нижче площини відповідно. Тому йому потрібно додаткове відображення для досягнення суперпозиції. Існує також вісь C 2, яка знаходиться в тих же місцях, що і вісь S 4.
Посібник з визначення груп точок
Маючи наявні у вас знання, ви можете однозначно ідентифікувати точкову групу молекули. Запорука успіху полягає в тому, що ви здатні бачити елементи симетрії в молекулі. Для цього потрібна практика. З достатньою практикою ви можете відразу визначити точкову групу молекули. До тих пір, ви можете використовувати напрямні, за якими ви можете слідувати, щоб визначити групу точок. Такий гід задає систематичні питання про наявність або відсутність елемента симетрії. Залежно від того, чи відповідаєте ви на питання так чи ні, ви можете слідувати керівництву в певному напрямку. Врешті-решт, відповівши на достатню кількість питань, керівництво приведе вас до відповідної групи точок. Таку діаграму ви можете побачити нижче (рис.2.2.86).
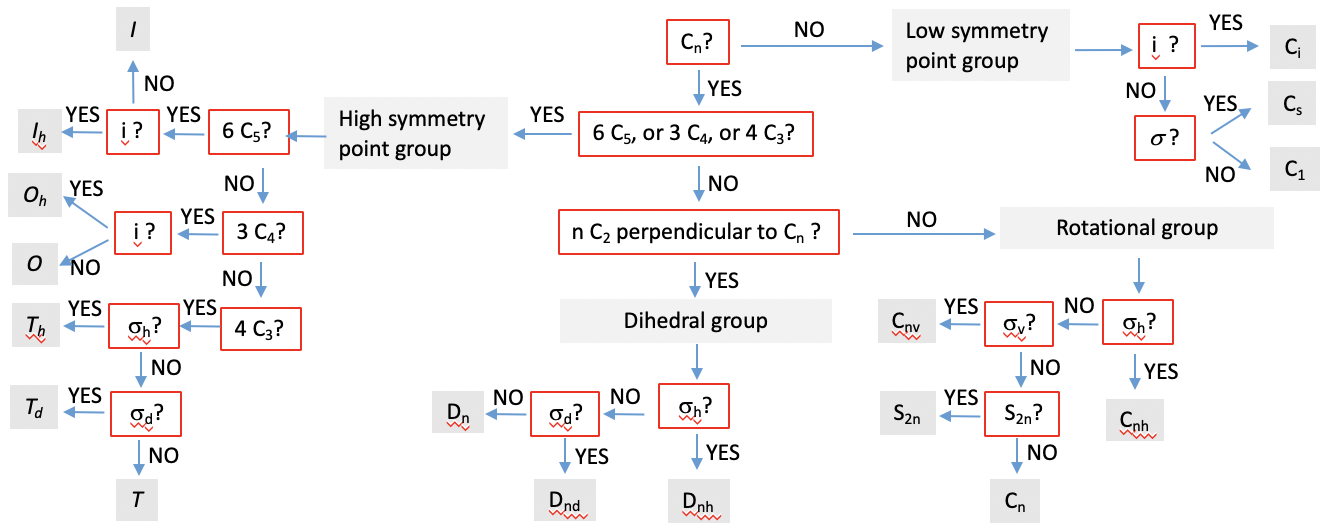
Ви можете спочатку запитати, чи є хоча б один C n присутній. Якщо ні, то молекула повинна знаходитися в групі точок низької симетрії. Якщо є центр інверсії, то група точок дорівнює C i. Якщо ні, ми можемо далі запитати, чи є дзеркальна площина. Якщо так, то це C s, а якщо ні група точок - C 1. Якщо група точок низької симетрії може бути виключена, то ми можемо запитати далі, чи є група точок високої симетрії. Це той випадок, коли присутні або 4C 3, 3C 4, або 6C 5 осі обертання, що стоять за чотиригранну, восьмигранну та ікосаедричну симетрію відповідно. Якщо в разі присутності С 5 є центр інверсії, то група точок дорівнює I h. Якщо ні, то це I. Аналогічно, якщо є осі 3С 4, і центр інверсії, група точок повинна бути O h. Якщо центру інверсії немає, то група точок - O. Якщо є осі 4C 3, група точок повинна бути типу T. Якщо додатково є горизонтальна дзеркальна площина, то група точок повинна бути T h. Якщо ні, ми можемо запитати далі, чи є двогранні дзеркальні площини. Якщо так, то група точок T d, інакше це T. Тепер ми перевірили для всіх груп точок високої симетрії.
Якщо групи точок високої симетрії можуть бути виключені, ми запитуємо, чи є n осей C 2 на додаток до головної осі C n. Якщо це так, то у нас повинна бути двогранна група типу D. Далі запитуємо, чи є горизонтальна дзеркальна площина. Якщо так, то група точок повинна бути D nh. Якщо ні, запитуємо, чи є двогранні дзеркальні площини. Якщо так, то група точок D nd. Якщо дзеркальних площин взагалі немає, то точкова група D n. Якщо крім C n немає n осей С 2, то група повинна бути або ротаційної групою, або групою неправильної обертання. Далі запитуємо, чи є горизонтальна дзеркальна площина. Якщо так, то точка група має тип C nh. Якщо ні, запитуємо, чи є вертикальні дзеркальні площини. Якщо так, то група точок C nv. Якщо це не так, ми запитуємо, чи є S 2n на додаток до C n. Якщо так, то група точок S 2n. Якщо ні, то це C n.
Приклад: Дибромонафтален
Давайте практикуємо керівництво по точковій групі на одному прикладі. Давайте розглянемо молекулу дибромонафталену (рис.2.2.87).
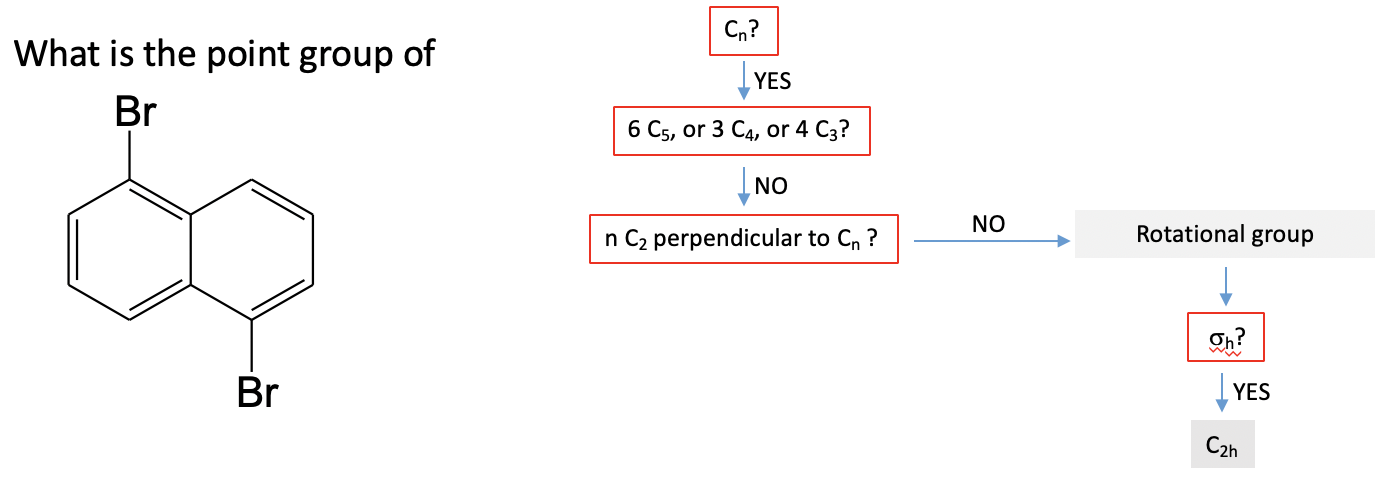
Перше питання, яке ми б запитали: Чи можете ви бачити принаймні одну правильну вісь обертання? Відповідь - так. Існує власна вісь обертання C 2, яка стоїть перпендикулярно площині молекули і проходить через центр зв'язку C-C, який поділяють два ароматичні кільця. Далі ми запитуємо: Є осі 6C 5, 3C 4 або 4C 3? Це явно не так, і, таким чином, ми не маємо групи точок високої симетрії. Далі ми можемо подумати про те, чи є осі 2C 2 на додаток до осей C 2, які ми вже знайшли. Відповідь - ні, тому група точок не може бути двогранною групою. Далі ми б запитали: Чи є горизонтальна дзеркальна площина. Це дійсно так. У площині молекули є горизонтальна дзеркальна площина. Він не рухає атоми навколо, але, як ми обговорювали раніше, дзеркало не потребує цього, щоб існувати. Це визначає групу точок як C 2h.
Групи кіральних точок
Хіральна група точок - це група точок, яка має лише належні операції обертання на додаток до ідентичності. Це еквівалентно твердженню про те, що в хіральній точковій групі не повинно існувати неправильних обертань. Це включає дзеркальні площини та центри інверсії, оскільки дзеркальна площина така ж, як S 1, а центр інверсії такий же, як S 2. Якщо молекула належить до групи хіральних точок, то вона має дзеркальне відображення, яке не може бути накладено з вихідною молекулою. Два дзеркальних зображення називаються енантіомерами. Прикладом може служити бромхлорфторметан. Можна побачити два енантіомера, розділених пунктиром (рис.2.2.88).
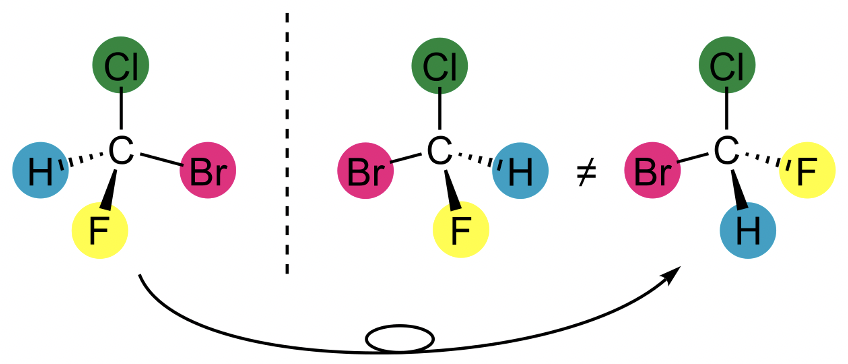
Пунктирна лінія являє собою дзеркальну площину. Зверніть увагу, що ця дзеркальна площина не є дзеркальною площиною в значенні елемента симетрії. Ви можете бачити, що дві молекули ліворуч і праворуч від дзеркальної площини є дзеркальними зображеннями, відповідними один одному. Молекули не можуть бути накладені, що означає, що вони є енантіомерами. Зверніть увагу, що молекула бромхлорфторметану в крайньому правому куті не є енантіомером до двох інших. Це та ж молекула, що і енантіомер в крайньому лівому куті. Нам потрібно лише обертати за годинниковою стрілкою навколо осі C-Cl, щоб дві молекули накладалися, що означає, що вони однакові.
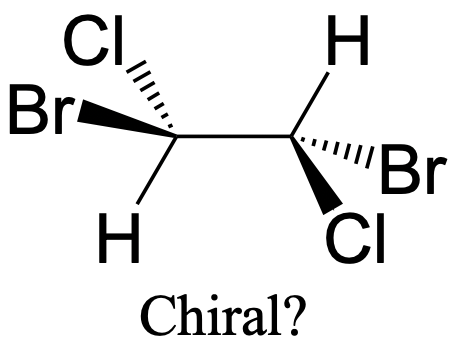
Слід зазначити, що той факт, що молекула має вуглець з чотирма різними замінниками, недостатньо, щоб зробити її хіральною молекулою. Молекула дибромодихлоретану, показана вище (рис. 2.2.89), має чотири різних замінника навколо атома вуглецю, але вона не є хіральною, оскільки посередині зв'язку С-С є інверсійним центром.
Хіральні групи точок високої симетрії
Хіральні групи не обов'язково повинні мати низьку симетрію, насправді обертальні підгрупи з високою симетрією I, O і T є хіральними групами, оскільки вони мають лише відповідні осі на додаток до ідентичності (рис. 2.2.90).
