Skip to main content
LibreTexts - Ukrayinska

4.3: Іспит 3

  1. Last updated
  2. Save as PDF
  • Page ID
    27772

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Завдання 1 (23 БАЛИ)

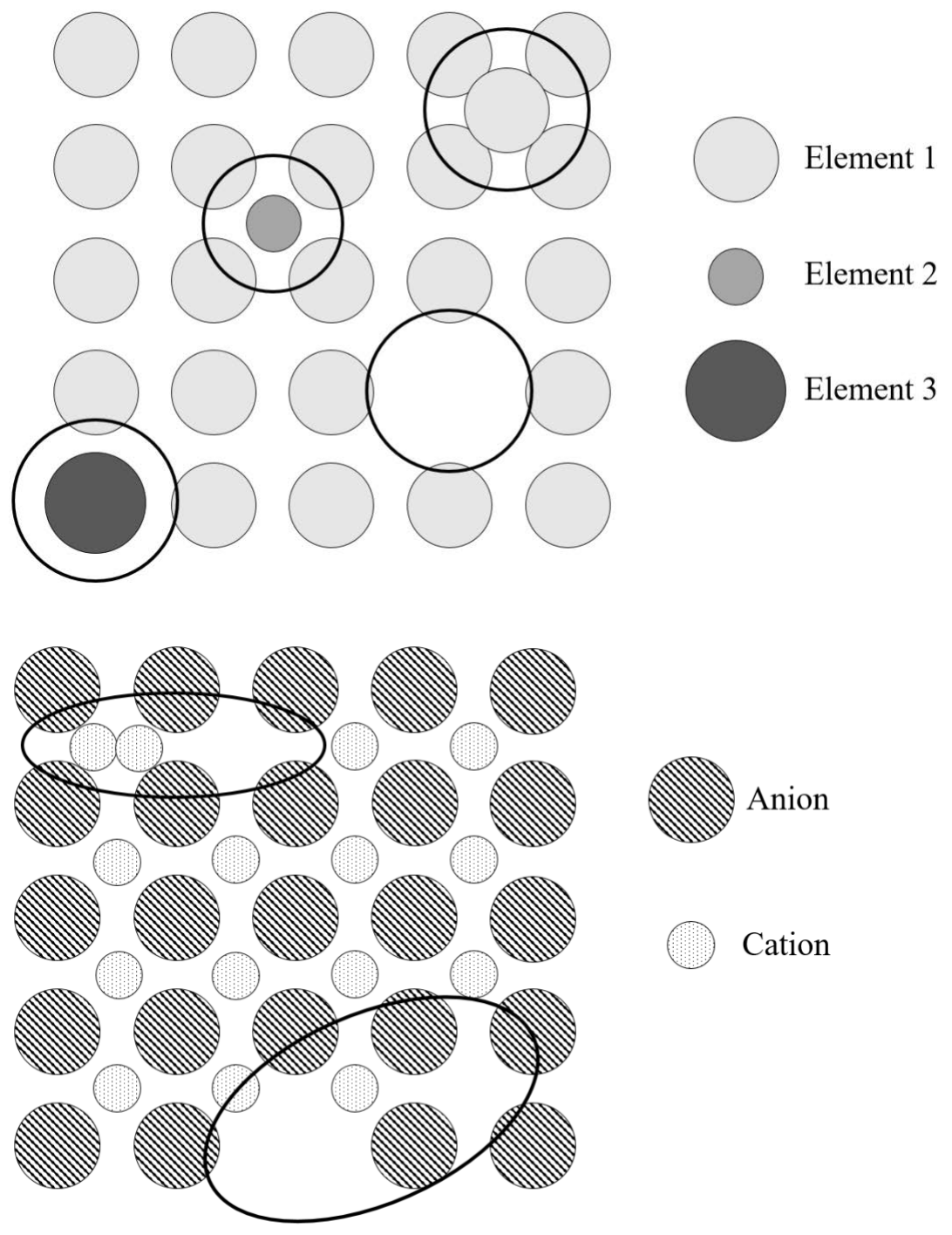
    а) У кристалічних твердих тілах 2, показаних нижче, є обведені шість різних точкових дефектів TOTAL. Позначте кожен дефект своїм найменуванням. (6 балів)

    Знімок екрана 2022-09-01 в 1.07.59 AM.png

    Ви вирішили купити кільце в ювелірному магазині вниз по Масовому пр. Спираючись на свої глибокі знання з матеріалознавства з 3.091, ви вирішите, що платинове кільце - це, безумовно, шлях. На жаль, ювелір закінчив ту школу по вулиці; ви засмучені їх твердженням, що кільце - це «бездефектна кристалічна платина». Давайте доведемо їх неправильно!

    б) Спочатку ви зважуєте кільце: це рівно 2 грами. Скільки атомів платини в кільці? (2 бали)

    в) Скільки атомних майданчиків знаходиться в кільці,\(\mathrm{N}_{\mathrm{Pt}}\)? (2 бали)

    г) Трохи холодно в магазині:\(11^{\circ} \mathrm{C}(284 \mathrm{~K})\). Припускаючи, що кільце знаходиться в тепловій рівновазі, розрахуйте загальну кількість вакансій\(\mathrm{N}_{\mathrm{v}}\), які ви очікували б при поточній температурі. Константа,\(A\), має значення 1,11. Припустимо, що енергія формування вакансії для\(\mathrm{Pt}\) є\(0.96 \mathrm{eV}\). (4 бали)

    д) Ювелір підкреслений вашими шаленими розрахунками і прагнуть довести, що вони не обманюють вас; вони поспішно вказують, що атоми, які прийшли з цих вакансій, ймовірно, сидять у міжсторінкових ділянках у решітці. Ви швидко підтягуєте папір, яка виміряла інтерстиціальну концентрацію в\(\mathrm{Pt}\).

    Примітка: одиницями концентрації інтерстиціального дефекту є моль/л.

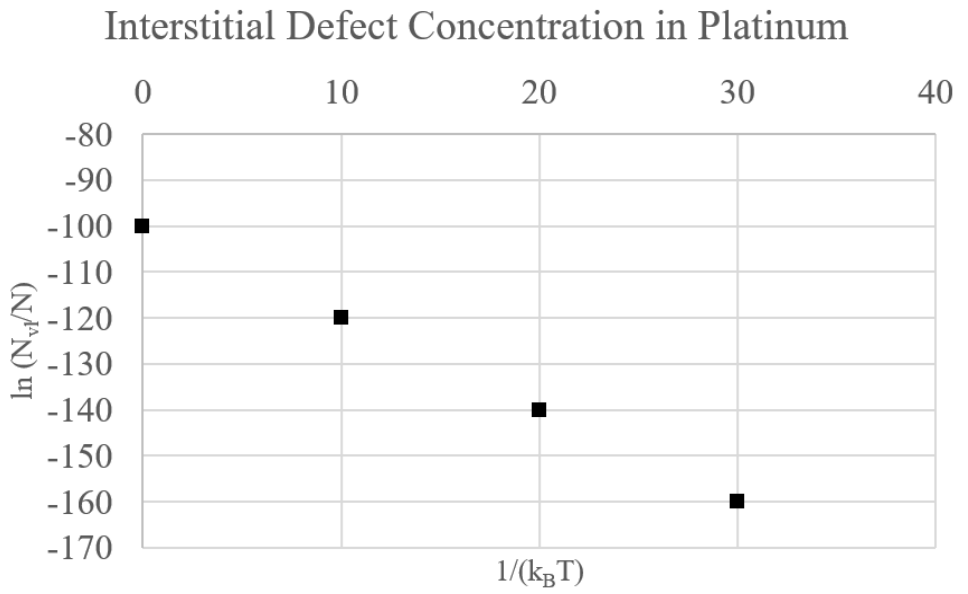
    Знімок екрана 2022-09-01 в 1.10.18 AM.png

    i) Оцініть енергію утворення (в Дж) інтерстиціального дефекту з ділянки. Як це порівнюється з енергією формування вакансії в\(\mathrm{Pt}\), яка була дана вище як\(0.96 \mathrm{eV}\)? Підказка: припустимо, що концентрація інтерстиціального дефекту слідує за відносинами Арреніуса. (5 балів)

    ii) Чи міг ювелір мати рацію, грунтуючись на енергії активації для міжстиціального формування та формування вакансій? Іншими словами, чи могли атоми з вакантних ділянок стати міжстиціальними дефектами? Поясніть свої міркування в одному реченні. (4 бали)

    Завдання 2 (20 БАЛІВ)

    а) Намалюйте наступне на наведених осях:

    i) Крива охолодження (молярний об'єм проти температури) для аморфного\(\mathrm{SiO}_2\) (3 бали)

    ii) Крива охолодження (молярний об'єм проти температури) для кристалічних\(\mathrm{SiO}_2\) (3 бали)

    Будь ласка, позначте криві\(\mathrm{i}\) і\(\mathrm{ii}\).

    Знімок екрана 2022-09-01 в 1.13.10 AM.png

    б) На вашій ділянці вище позначте:

    i) температура плавлення (и) (2 бали)

    ii) температура (и) скляного переходу (и) (2 бали)

    в) Перелічіть ДВА способи зміни температури склопереходу. (4 бали)

    г) Загартоване скло проявляє підвищену міцність в порівнянні зі звичайним склом. Розглянемо зріз, зроблений поперек аркуша загартованого скла:

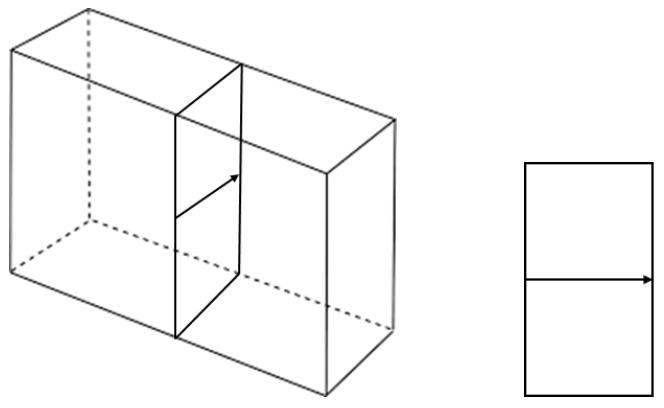
    Знімок екрана 2022-09-01 в 1.14.10 AM.png

    Що стосується вашої ділянки в а), поясніть, як змінюється молярний об'єм по всьому зрізу. (4 бали)

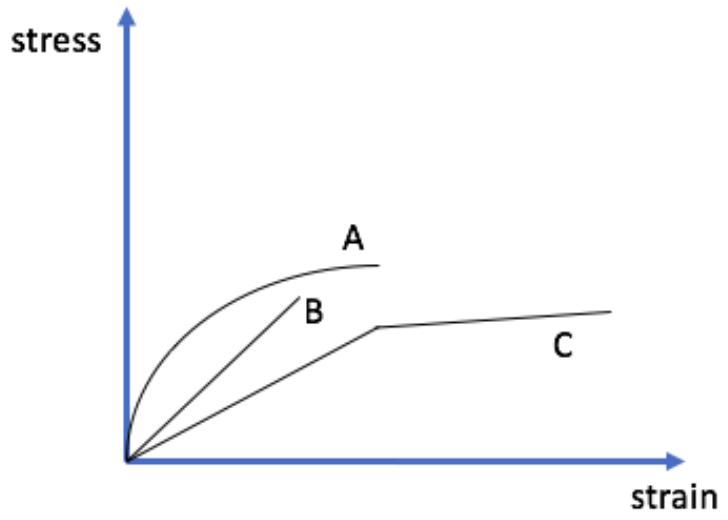
    д) Яка з наступних кривих напруження-деформації може відповідати загартованому склу вище? Обведіть букву, відповідну обраній кривій. (2 бали)

    Знімок екрана 2022-09-01 в 1.14.51 AM.png

    Завдання 3 (20 БАЛІВ)

    У GB8 ми досліджували вплив підкислення океану на птероподи, розглядаючи розчинення\(\mathrm{CaCO}_3\) в розчині лимонної кислоти. Зараз ми розглянемо аналогічний процес, але використовуючи замість нього плавикову кислоту. Плавикова кислота\(\mathrm{HF}\), має більш високу константу дисоціації кислоти, ніж лимонна кислота.

    а) Випишіть реакцію дисоціації кислоти на плавикову кислоту. Позначте сполучені пари кислота/основи. (5 балів)

    б) Яка концентрація (М) розчину, що містить\(0.05 \mathrm{~g}\)\(\mathrm{HF}\) в\(0.1 \mathrm{~L} \mathrm{H}_2 \mathrm{O}\)? (3 бали)

    в) Якщо константа дисоціації кислоти для плавикової кислоти є\(\mathrm{K}_{\mathrm{a}}=7.2 \times 10^{-4}\), що таке розчин з частини б)?\(\mathrm{pH}\) (4 бали)

    д) Якби ми дали вам плавикову кислоту,\(\left(\mathrm{K}_{\mathrm{a}}=7.2 \times 10^{-4}\right)\) а не лимонну кислоту\(\left(\mathrm{K}_{\mathrm{a}}=1.8 \times 10^{-5}\right)\) в сумці гуді, чи очікували б ви, що оболонки розчиняються швидше чи повільніше? Коротко поясніть, чому. (4 бали)

    f) Поясніть, що станеться\(\mathrm{pH}\) з розчином плавикової кислоти, якщо він буде сидіти в\(\mathrm{CO}_2\) середовищі протягом декількох годин, і чому. (4 бали)

    Завдання 4 (21 БАЛ)

    Щоб компенсувати частину кисню, споживаного спалюванням свічки в одну з ваших численних дат у п'ятницю ввечері, ви вирішили запустити реакцію, яка виробляє\(\mathrm{O}_2\) газ якомога швидше. Ви згадаєте два варіанти:

    \((p) 2 \mathrm{NO}_2 \rightarrow 2 \mathrm{NO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \quad \mathrm{OR} \quad (q) \mathrm{O}_3+\mathrm{Cl} \rightarrow \mathrm{ClO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g})\)

    Ви в змозі знайти деяку інформацію про реакцію\((p)\): її норма закон

    \(\text { rate }=\mathrm{k}\left[\mathrm{NO}_2\right]\)

    (Примітка: реакції\(p\) і\(q\) мають однакове числове значення для їх констант реакції)

    Випробування #

    [\(\mathrm{O}_3\)]

    \(\mathrm{M}\)

    [\(\mathrm{Cl}\)]

    \(\mathrm{M}\)

    норма

    \(\mathrm{M}/\mathrm{s}\)
    1 \ (\ матрм {O} _3\)]\(\mathrm{M}\) «>0.07 \ (\ матрм {Cl}\)]\(\mathrm{M}\) «>0,25 \ (\ mathrm {M}/\ mathrm {s}\) ">10
    2 \ (\ матрм {O} _3\)]\(\mathrm{M}\) «>0.14 \ (\ матрм {Cl}\)]\(\mathrm{M}\) «>0,25 \ (\ mathrm {M}/\ mathrm {s}\) ">20
    3 \ (\ матрм {O} _3\)]\(\mathrm{M}\) «>0.07 \ (\ mathrm {Cl}\)]\(\mathrm{M}\) «>0.5 \ (\ mathrm {M}/\ mathrm {s}\) ">20

    а) Використовуйте експериментальні дані в таблиці вище про реакцію (\(q\)) для визначення її:

    i. нормове право (5 балів)

    II. Загальний порядок (2 бали)

    iii. Значення\(\mathrm{k}\), константа реакції (5 балів)

    б) Побудувати лінійний варіант інтегрованого закону ставки, який описує\(2 \mathrm{NO}_2 \rightarrow 2 \mathrm{NO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g})\). Позначте осі,\(y\) перехоплення та нахил. (5 балів)

    Знімок екрана 2022-09-01 в 12.51.03 PM.png

    в) Якщо у вас є 2 моль\(\mathrm{NO}_2, 1 \mathrm{~mol} \mathrm{of} \mathrm{Cl}\), і\(1 \mathrm{~mol}\) з\(\mathrm{O}_3\) доступних (але ви можете запустити тільки одну реакцію), яку реакцію ви б вибрали для отримання кисню найшвидше? Обґрунтуйте свою відповідь ОДНИМ реченням. (4 бали)

    Завдання 5 (16 БАЛІВ)

    Ваш науковий керівник хоче, щоб ви охарактеризували два чистих елементарних порошку, які вона знайшла в задній частині лабораторії. На жаль, час на машині XRD дуже обмежений; щоб заощадити час, ви змішуєте ОБИДВА ПОРОШКИ разом і виконуєте XRD на суміші.

    Ви отримуєте наступний графік інтенсивності (підраховує) проти\(2 \theta\) (градусів):

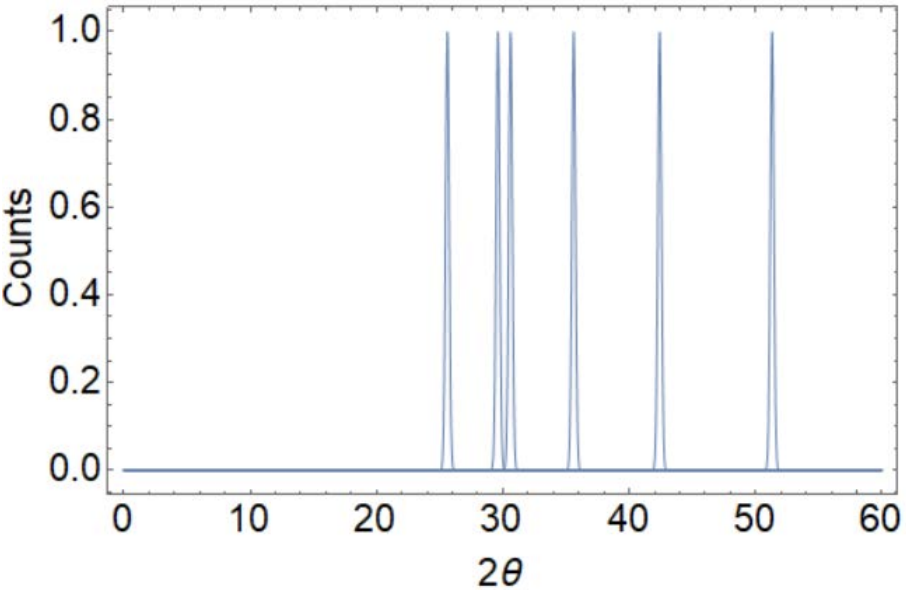
    Знімок екрана 2022-09-01 в 12.52.12 PM.png

    З сюжету у вас є наступні дані, які допоможуть ідентифікувати зразки. Можливо, вам буде корисно додати стовпці, щоб допомогти вашому мисленню (неоцінене).

    \(2 \theta\)(градуси) \((\sin \theta)^2\)
    \ (2\ тета\) (градуси) ">25,6 \ (\ sin\ тета) ^2\) ">0.049
    \ (2\ тета\) (градуси) ">29.6 \ (\ sin\ тета) ^2\) ">0.065
    \ (2\ тета\) (градуси) ">30.7 \ (\ sin\ тета) ^2\) ">0,070
    \ (2\ тета\) (градуси) ">35.6 \ (\ sin\ тета) ^2\) ">0.093
    \ (2\ тета\) (градуси) ">42.4 \ (\ sin\ тета) ^2\) ">0.131
    \ (2\ тета\) (градуси) ">51.3 \ ((\ гріх\ тета) ^2\) ">0.187

    а) Використовуйте правила відбору для визначення кристалічних структур зразків (8 балів) Примітка: Припустимо, зразок 1 відповідає елементу з найнижчим 2-тета-піком.

     

    Зразок 1: ___________________________ Зразок 2: _______________________________

    б) Які константи решітки зразків? Використано мідне k-альфа-випромінювання (довжина хвилі = 1,54 ангстреми). Покажіть своє мислення! (8 балів)

    Зразок 1: ___________________________ Зразок 2: _______________________________