7.2: Зміни стану та енергетика

Last updated
Save as PDF

Page ID: 22775

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Результати навчання

Визначте, чи енергія споживається або виділяється під час зміни фази.
Обчисліть кількість енергії, споживаної або виділеної при зміні фази.
Визнайте, що ентальпії випаровування та конденсації рівні за величиною, але протилежні за знаком.
Визнайте, що ентальпії злиття та заморожування рівні за величиною, але протилежні за знаком.

Крива нагріву

Коли теплова енергія подається до твердого тіла (як лід) зі стійкою швидкістю за допомогою електричної нагрівальної котушки, ми виявляємо, що температура стабільно піднімається, поки не буде досягнута температура плавлення і не стануть очевидними перші ознаки утворення рідини. Після цього, незважаючи на те, що ми все ще подаємо теплову енергію в систему, температура залишається постійною до тих пір, поки присутні як рідина, так і тверда речовина. На графіку нижче це представлено плоскою лінією, де до льоду додається енергія, але ніяких змін температури не відбувається. Вся енергія, що додається в систему на цьому етапі, використовується для перетворення твердого льоду в рідку воду.

Після того, як весь зразок знаходиться в рідкій фазі, додавання енергії тепер збільшує температуру, поки не буде досягнута температура кипіння і не будуть помічені перші ознаки газоутворення. Температура залишається постійною, навіть якщо в систему додається енергія. Енергія використовується для перетворення рідини в газ. Після того, як весь зразок знаходиться в газовій фазі, можна додати додаткову енергію для підвищення температури газу.

Малюнок\(\PageIndex{1}\): Крива нагріву води на 1 атм. Консорціумом коледжів спільноти з біонауки (власна робота) [CC BY 3.0 (http://creativecommons.org/licenses/by/3.0)], через Вікісховище

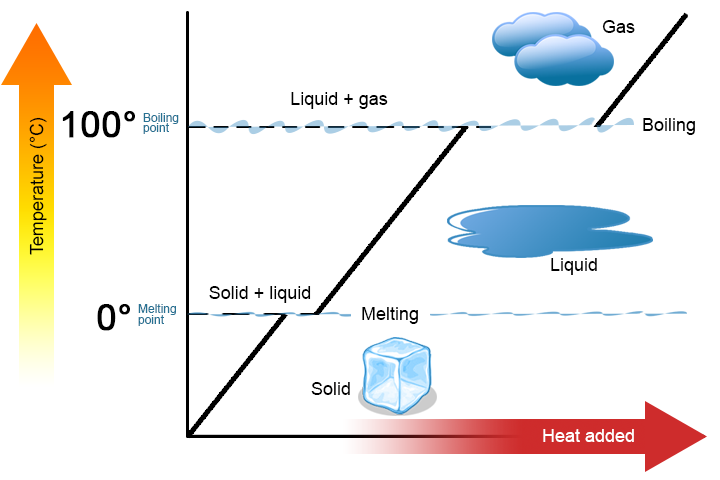
Ця макроскопічна поведінка досить чітко демонструє, що енергія повинна подаватися до твердого тіла, щоб розплавити або випаровувати його. На мікроскопічному рівні плавлення або випаровування передбачає відділення молекул, які притягуються один до одного. Кількість енергії, необхідної для поділу молекул, пропорційна міжмолекулярним силам між молекулами.

Ентальпія

Теплова енергія, яку тверда речовина поглинає, коли вона плавиться, називається ентальпією плавлення (ΔH _fus) або теплотою плавлення і зазвичай цитується на молярній основі. (Слово злиття означає те ж саме, що і «плавлення».) Коли 1 моль льоду, наприклад, розтане, ми знаходимо з експерименту, що потрібно 6,01 кДж енергії. Таким чином, молярна ентальпія злиття льоду становить +6,01 кДж на моль (\(\dfrac{6.01\;kJ}{mol}\)), і ми можемо записати

\[\text{H}_{2}\text{O}(s) \rightarrow \text{H}_{2}\text{O}(l)\]

\[\triangle H_{fus} = \dfrac{6.01\;kJ}{mol}\]

Якщо два молі води розтоплюються, то для цього буде потрібно в два рази більше енергії (див. Нижче). Кількість енергії, необхідної для розплавлення речовини, буде залежати від кількості речовини.

\(2\;mol\times \dfrac{6.01\;kJ}{mol}=\dfrac{12.0\;kJ}{mol}\)

Вибрані молярні ентальпії злиття наведені в табл\(\PageIndex{1}\). Тверді речовини, такі як лід, які мають сильні міжмолекулярні сили, мають набагато вищі значення, ніж такі, як CH ₄ зі слабкими.

Коли рідина кип'ятиться (або випаровується), потрібна енергія для переміщення молекул один від одного, щоб перейти від рідкої фази до газової фази. Енергія, яку поглинає рідина, коли вона випаровується, відома як ентальпія випаровування (ΔH _vap). У випадку з водою молярна ентальпія випаровування становить (\(\dfrac{40.67\;kJ}{mol}\)). Іншими словами

\[\text{H}_{2}\text{O}(s) \rightarrow \text{H}_{2}\text{O}(l)\]

\[\triangle H_{vap} = 40.67 \dfrac {\text{kJ}}{\text{mol}}\]

Теплова енергія поглинається для випаровування рідини, оскільки молекули, які утримуються між собою міжмолекулярними силами в рідині, розділяються в міру утворення газу. Такий поділ вимагає енергії. Як і при плавленні, кількість енергії, необхідної для випаровування речовини, пропорційна кількості присутньої речовини. Чим більше рідини, тим більше енергії потрібно для її випаровування.

Взагалі необхідна енергія відрізняється від однієї рідини до іншої залежно від величини міжмолекулярних сил. Ми можемо очікувати, що рідини з сильними міжмолекулярними силами матимуть більші ентальпії випаровування. Дивіться приклади в таблиці нижче. Відзначимо, що ентальпія випаровування речовини завжди вище, ніж його ентальпія злиття. Коли тверда речовина плавиться, молекули не відокремлюються один від одного майже в тій же мірі, як коли рідина закипає.

Температура плавлення і кипіння наведені в одиницях Кельвіна (\(K = T_{^{\circ}C}\;+\;273.15 \))

Таблиця\(\PageIndex{1}\): Молярні ентальпії плавлення та вапоризації обраних речовин.
Речовина	Формула	\(\triangle H_{fus}\) (\(\dfrac{kJ}{mol}\))	Точка плавлення (K)	\(\triangle H_{vap}\) (\(\dfrac{kJ}{mol}\))	Точка кипіння (K)
неонові	Ne	0,33	24	1.80	27
кисень	О ₂	0,44	54	6.82	90.2
метан	СН ₄	0,94	90.7	8.18	112
етану	С ₂ Ч ₆	2.85	90.0	14.72	184
хлору	Сл ₂	6.40	172.2	20.41	239
чотирихлористий вуглець	ККл ₄	2.67	250.0	30.00	350
вода*	Н ₂ О	6.01	273.1	40.7	373.1
n -нонан	З ₉ Ч ₂₀	19.3	353	40.5	491
свинець	Пб	4.77	601	178	2022
нашатирний спирт	NH ₃	5.636	195	23.35	240
етанолу	СН ₃ СООН	4.9	159	38.56	351

* http://www1.lsbu.ac.uk/water/data.html

Приклад\(\PageIndex{1}\): Heat Energy

Розрахуйте теплову енергію, необхідну для (а) випаровування 100. г свинцю, (б) розплаву 100. г свинцю, (в) випаровування 100. г води і (г) розтопити 100. г води.

Рішення

(а) Для випаровування 100 г свинцю:

\ [\ текст {Pb} (л)\ стрілка вправо\ текст {Pb} (g)\;\;\;\;\;\;\;\;\;\;
\ трикутник H_ {vap} = 178\ dfrac {кДж} {моль}\]

\[100.\;g\times\dfrac {1\;mol\;\text{Pb}}{207.2\;g\;\text{Pb}}\times \dfrac{178\;{kJ}}{mol} = 85.9\; kJ\]

(б) Розплавити 100 г свинцю:

\[\text{Pb}(s) \rightarrow\text{Pb}(l)\;\;\;\;\;\;\;\;\;\;\triangle H_{fus} = 4.77 \dfrac {kJ}{mol}\]

\[100.\;g\times\dfrac {1\;mol\;\text{Pb}}{207.2\;g\;\text{Pb}}\times \dfrac{4.77\;{kJ}}{mol} = 2.30\; kJ\]

\[\text{H}_2\text{O}(s) \rightarrow\text{H}_2\text{O}(l)\;\;\;\;\;\;\;\;\;\;\triangle H_{vap} =40.657\dfrac {kJ}{mol}\]

\[100.\;g\times\dfrac {1\;mol\;\text{H}_2\text{O}}{18.0\;g\;\text{H}_2\text{O}}\times \dfrac{40.657\;{kJ}}{mol} = 226\; kJ\]

(d) Розтопити 100 г води:

\[\text{H}_2\text{O}(s) \rightarrow\text{H}_2\text{O}(l)\;\;\;\;\;\;\;\;\;\;\triangle H_{fus} = 6.01 \dfrac {kJ}{mol}\]

\[100.\;g\times\dfrac {1\;mol\;\text{H}_2\text{O}}{18.0\;g\;\text{H}_2\text{O}}\times \dfrac{6.01\;{kJ}}{mol} = 33.4\; kJ\]

Це може бути дивно, що тепло, необхідне для розплавлення або випаровування 100 г свинцю, набагато менше, ніж потрібно для розплавлення або випаровування води. По-перше, температура, при якій речовина плавиться, не має нічого спільного з ентальпією плавлення. Пам'ятайте, ми дивимося лише на енергію, необхідну для зміни фази, а не енергію, необхідну для отримання речовини до температури плавлення або кипіння.

Також відзначимо, що ентальпії синтезу і випаровування наведені як кДж на моль. Хоча вода і свинець мають однакову масу, молі кожної речовини дуже різні (5,5 моля води проти 0,48 моля свинцю).

Заморожування та конденсація

Обговорення тут було зосереджено на плавленні (плавленні) та випаровуванні. А як щодо замерзання та конденсації? Розплавлення (від твердого до рідкого) і заморожування (від рідини до твердого) є протилежними процесами. В результаті величина енергії для кожного однакова, але знак різний. При синтезі енергія є позитивним значенням, оскільки вона ендотермічна (споживає енергію), тоді як енергія для заморожування негативна, оскільки це екзотермічний процес (вивільнення енергії).

Давайте порівняємо ентальпії плавлення і заморожування для метану. Обидва значення мають однакову величину 0,94, але мають протилежний знак.

\(\triangle H_{fusion}=0.94\;\dfrac{kJ}{mol}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\triangle H_{freezing}=-0.94\;\dfrac{kJ}{mol}\)

Це ж поняття стосується випаровування (рідина до газу) і конденсації (газ до рідини). Енергія витрачається при випаровуванні (позитивна енергія) і виділяється при конденсації (негативна енергія). Ентальпії випаровування та конденсації рівні за величиною, але протилежні за знаком.

\(\triangle H_{vaporization}=8.18\;\dfrac{kJ}{mol}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\triangle H_{condensation}=-8.18\;\dfrac{kJ}{mol}\)

Енергія витрачається на зміну речовини з твердого на рідке на газ. Енергія виділяється для зміни речовини з газу на рідке на тверде.