32.3: Методи активації нейтронів

Last updated
Save as PDF

Page ID: 27157

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Мало аналітів є природним радіоактивним. Однак для багатьох аналітів ми можемо індукувати радіоактивність, опромінюючи зразок нейтронами в процесі, який називається аналізом активації нейтронів (NAA). Радіоактивний елемент, утворений при активації нейтронів, розпадається до стійкого ізотопу, випромінюючи гамма-промінь, і, можливо, і інші ядерні частинки. Швидкість випромінювання гамма-випромінювання пропорційна початковій концентрації аналіту в зразку. Наприклад, якщо ми помістимо зразок, що містить нерадіоактивний,\(_{13}^{27}\text{Al}\) в ядерний реактор і опромінюємо його нейтронами, відбувається наступна ядерна реакція.

\[_{13}^{27} \mathrm{Al}+_{0}^{1} \mathrm{n} \longrightarrow_{13}^{28} \mathrm{Al} \nonumber \]

Радіоактивний ізотоп ²⁸ Al має характерний процес розпаду, який включає вивільнення бета-частинки і гамма-променя.

\[_{13}^{28} \mathrm{Al} \longrightarrow_{14}^{28} \mathrm{Al}+_{-1}^{0} \beta + \gamma \nonumber \]

Коли опромінення завершено, ми видаляємо зразок з ядерного реактора, дозволяємо будь-яким короткочасним радіоактивним перешкодам розпастися на задній план, і вимірюємо швидкість випромінювання гамма-випромінювання.

Початкова активність в кінці опромінення залежить від кількості атомів, які присутні. Це, в свою чергу, дорівнює різниці між швидкістю утворення для\(_{13}^{28}\text{Al}\) і швидкістю її розпаду

\[\frac {dN_{_{13}^{28} \text{Al}}} {dt} = \Phi \sigma N_{_{13}^{27} \text{Al}} - \lambda N_{_{13}^{28} \text{Al}} \label{13.5} \]

де\(\Phi\) - потік нейтронів і\(\sigma\) перетин реакції, або ймовірність того, що\(_{13}^{27}\text{Al}\) ядро захоплює нейтрон. Інтегруючи рівняння\ ref {13.5} за час опромінення, t _i, і множення на\(\lambda\) дає початкову активність, A ₀, в кінці опромінення як

\[A_0 = \lambda N_{_{13}^{28}\text{Al}} = \Phi \sigma N_{_{13}^{27}\text{Al}} (1-e^{-kt}) \nonumber \]

Якщо ми знаємо значення для A ₀,,\(\Phi\)\(\sigma\)\(\lambda\), і t _i, то ми можемо обчислити кількість атомів\(_{13}^{27}\text{Al}\) спочатку присутніх у зразку.

Більш простий підхід полягає у використанні одного або декількох зовнішніх стандартів. Допускаючи\((A_0)_x\) і\((A_0)_s\) представляючи початкову активність аналіта в невідомому та зовнішньому стандарті, а також дозволяючи\(w_x\) та\(w_s\) представляючи вагу аналіта в невідомому та зовнішньому стандарті, отримаємо наступну пару рівнянь

\[\left(A_{0}\right)_{x}=k w_{x} \label{13.6} \]

\[\left(A_{0}\right)_{s}=k w_{s} \label{13.7} \]

що ми можемо вирішити для визначення маси аналіта в зразку.

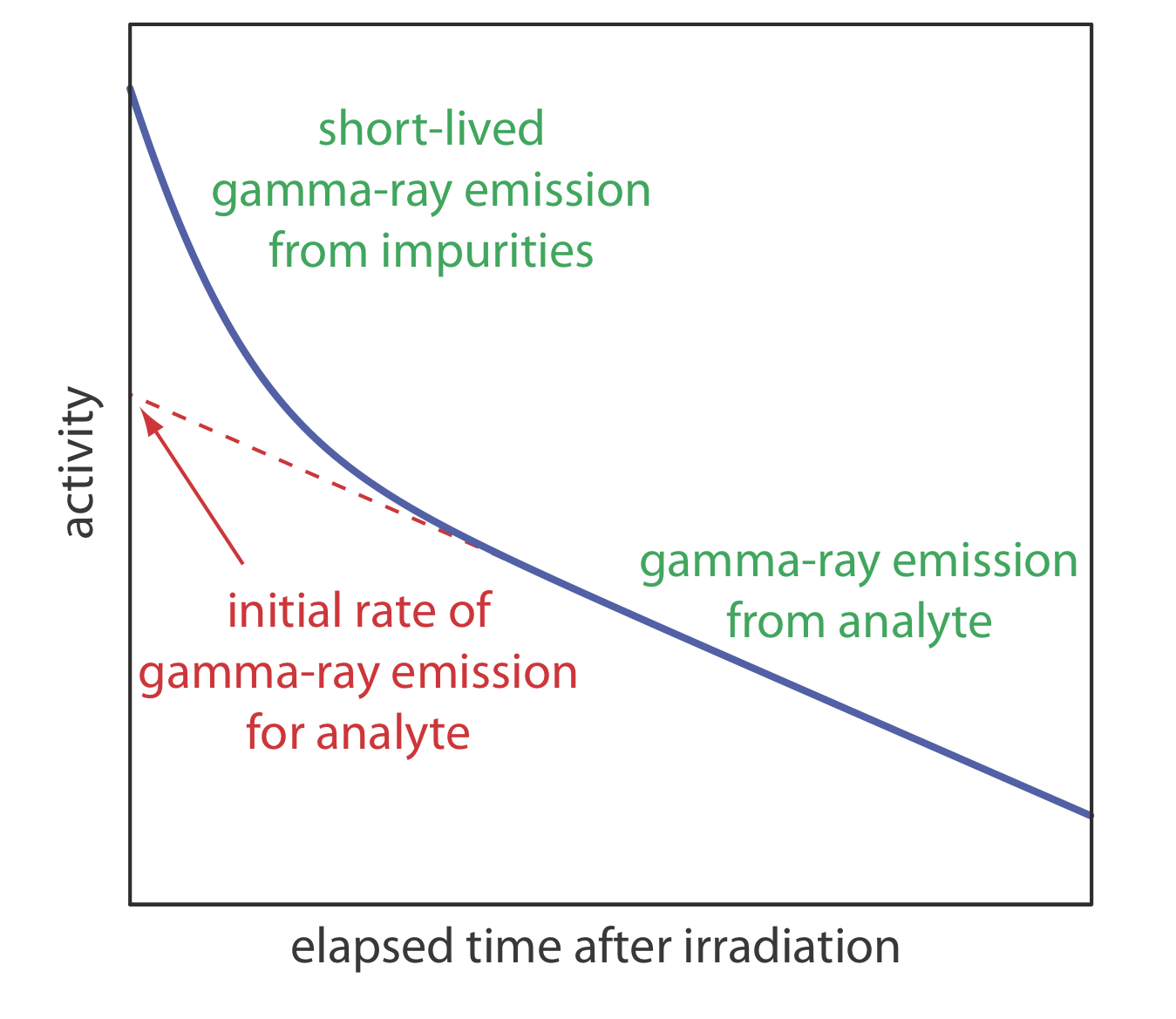
Як зазначалося раніше, випромінювання гамма-променів вимірюється після періоду, протягом якого ми дозволяємо короткочасним перешкодам розпастися на задній план. Як показано на рисунку Template:index, ми визначаємо початкову активність вибірки або еталону шляхом екстраполяції кривої активності проти часу назад до t = 0. Крім того, якщо ми опромінюємо зразок і стандарт одночасно, і якщо ми вимірюємо їх діяльність одночасно, то ми можемо замінити ці дії на (A ₀) _x і (A ₀) _s. Це стратегія, яка використовується в наступному прикладі.

Показано графік часу, що минув після опромінення проти активності. Короткочасне випромінювання гамма-променів внаслідок домішок спричиняє різке падіння активності безпосередньо після опромінення, перш ніж слідувати лінійному падінню активності від випромінювання гамма-променів з аналіту. — Рисунок Template:index. Графік випромінювання гамма-випромінювання як функція часу показує, як визначається початкова активність аналіта.

Приклад Template:index

Концентрація Mn в сталі визначається аналізом активації нейтронів методом зовнішніх стандартів. Зразок 1,000 г невідомого зразка сталі і 0,950-г зразка стандартної сталі, яка, як відомо, містить 0,463% w/w Mn опромінюються нейтронами протягом 10 ч в ядерному реакторі. Після 40-хвилинної затримки випромінювання гамма-випромінювання становить 2542 cpm (відраховується в хвилину) для невідомого та 1984 cpm для зовнішнього стандарту. Що таке %w/w Mn у невідомому зразку сталі?

Рішення

Об'єднання рівнянь\ ref {13.6} і\ ref {13.7} дає

\[w_{x}=\frac{A_{x}}{A_{s}} \times w_{s} \nonumber \]

Вага Mn в зовнішньому стандарті дорівнює

\[w_{s}=\frac{0.00463 \text{ g } \text{Mn}}{\text{ g } \text { steel }} \times 0.950 \text{ g} \text { steel }=0.00440 \text{ g} \text{ Mn} \nonumber \]

Підстановка в вищевказане рівняння дає

\[w_{x}=\frac{2542 \text{ cpm}}{1984 \text{ cpm}} \times 0.00440 \text{ g} \text{ Mn}=0.00564 \text{ g} \text{ Mn} \nonumber \]

Оскільки початкова маса сталі становить 1.000 г, %w/w Mn становить 0,564%.

Серед переваг нейтронної активації є її застосовність практично до всіх елементів таблиці Менделєєва і те, що вона неруйнівна для зразка. Отже, НАА є важливим прийомом аналізу археологічних та криміналістичних зразків, а також творів мистецтва.